Post

머신러닝 모델을 해석할 때 주의해야 할 8가지

Posted
Preview Image
By pizzathiefz 27 min read

General Pitfalls of Model-Agnostic Interpretation Methods for Machine Learning Models (2021) 를 읽어보았습니다.

PFI, LIME, SHAP, PDP와 같은 머신러닝 모델을 해석하기 위한 방법론들을 IML(Interpretable Machine Learning)이라고 합니다. 오늘은 IML을 사용할 때 주의해야 할 점과 겪을 수 있는 문제별로 대체해서 사용할 수 있는 방법론 등을 소개해보겠습니다. 여러 모로 실무자들이 참고하기 좋은 힌트들이 많은 논문이었습니다.

1. 하나의 방법이 다 들어맞을 거라는 착각

각각의 IML은 주어진 모델과 데이터에 대해 특정 부분에 집중한 인사이트를 제공할 뿐입니다. 특히 해석가능성(interpretability)이란 상당히 여러 개념을 포괄할 수 있는 umbrella term이고, 어떤 모델과 어떤 데이터인지에 따라 적합한 방법을 써야 합니다.

예컨대 각 피쳐가 얼마나 중요한지 수치화하거나 등수를 매기고 싶을 때, PFI와 SHAP의 결과는 매우 달라질 수 있습니다. 모델의 일반화 에러를 줄이는데 기여하는 피쳐를 찾고 싶다 하면 loss 기반으로 작동하는 PFI를 쓰는 게 맞고, 만약 모델의 성능과 무관하게 모델이 각 데이터의 예측이나 분류에 대해 어떤 피쳐에 의존하느냐를 보고 싶으면 PFI보단 SHAP가 적절하죠.

타겟 데이터(Y)를 모든 X와 전혀 상관이 없도록 데이터를 생성했다고 칩시다. 이 경우, 모든 피쳐들은 다 노이즈이고 타겟을 ‘잘’ 예측하는 데(즉 일반화 에러를 줄이는 데) 사용될 수 없습니다. 따라서 이 피쳐들의 PFI는 모두 낮게 나옵니다. 그럼에도 불구하고 모델을 학습시키면, 모델은 어쨌든 데이터를 사용해서(특히 허위 상관이 있는 피쳐들에 의존해서) 예측을 하긴 할 것입니다. 스코어는 안 좋겠지만. 이런 경우에 PFI와는 달리 일부 피쳐의 SHAP 중요도는 높게 나오는 걸 확인할 수 있습니다.

💡 제안:

  • 실제 분석이 이루어지기 전에 맥락에 맞는 해석의 목표를 잘 정의하고, 그에 맞는 방법론을 찾기 (SHAP 하나 배웠다고 해석 하고 싶을 때마다 주구장창 SHAP만 쓰지 말기…!)


2. 모델 Fit이 안 좋은데 무슨 해석을

애초에 모델 자체가 피팅이 잘 안 된 경우(underfitting이든 overfitting이든) 각 피쳐의 진짜 효과나 중요도를 알기 어렵습니다. 모델 자체가 데이터가 만들어진 실제 프로세스(ground truth)를 잘 알고 있지 못하기 때문입니다. 엄밀히 따지면 모델을 해석하는 것과 실제 데이터 생성 프로세스를 알아내는 건 다른 일이고, 사실 흔히 말하는 XAI의 목적은 전자에 가까운데 실무에서는 후자를 위해서 사용할 때가 많습니다. 우리가 데이터를 써서 이 모델을 만들었으니, 그 모델을 해석하면서 데이터에 대한 인사이트를 알아내고 싶다는 거죠. 하지만 모델이 좋아야만 해석도 좋아질 수 있습니다. 모델이 데이터 생성 프로세스를 충분히 근사해야지만 해석 또한 그 프로세스에 대한 인사이트를 제공해주는 것입니다.

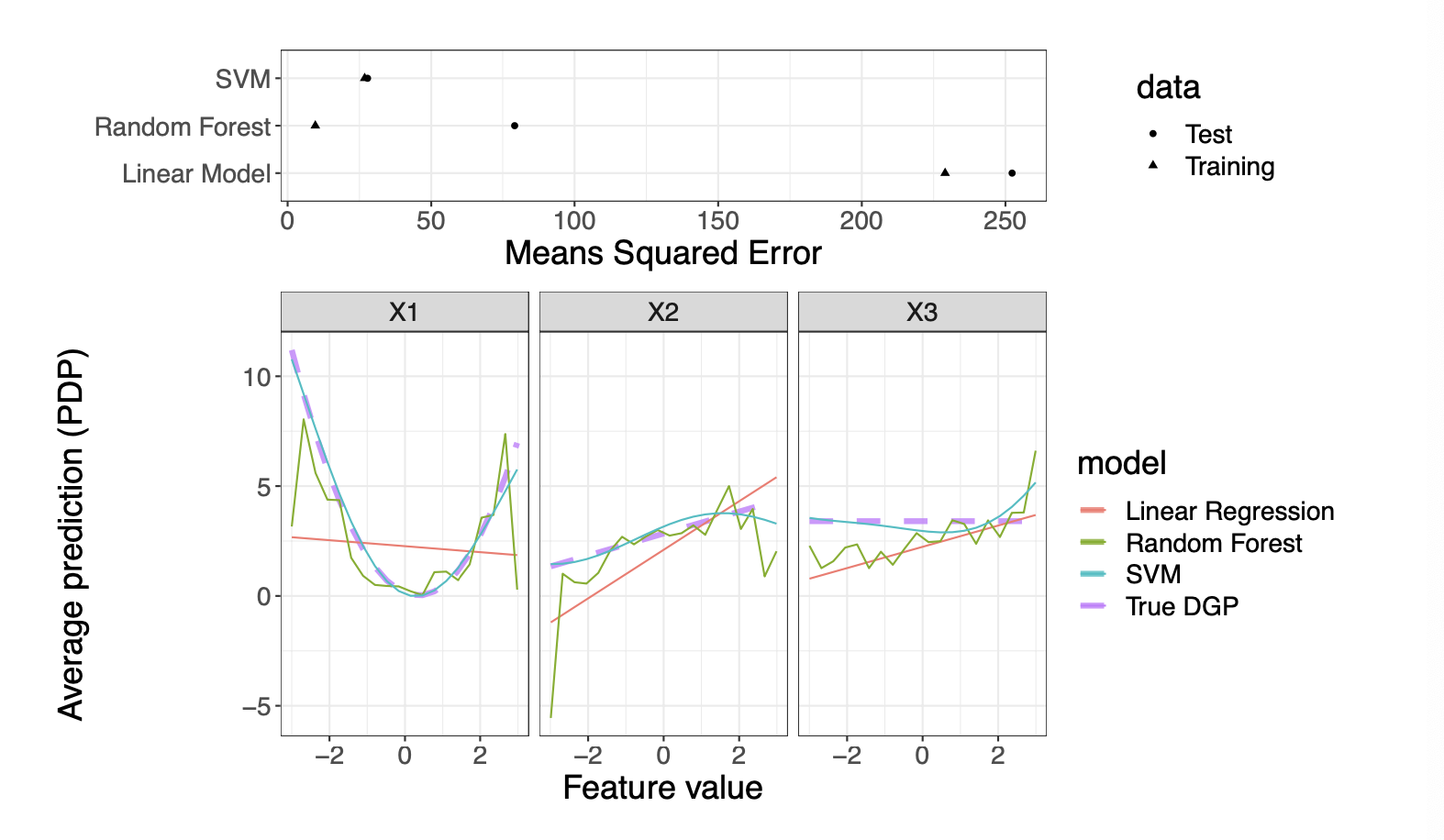
  • 첫번째 그림: 3개의 모델(SVM, 랜덤포레스트, 선형회귀)의 Test/Training MSE를 보여줌
    • SVM은 둘 다 괜찮고, 랜덤포레스트는 overfitted, 선형회귀는 underfitted 된 걸 알 수 있음
  • 두번째 그림: 각 모델의 PDP plot
    • 이 데이터는 $Y=X_1^2 + X_2 -5X_1X_2 + \epsilon$ ($\epsilon$은 정규분포에서 뽑은 노이즈) 이렇게 생성되었고 보라색 선(True data genearting process)에서 확인할 수 있음
    • 각 모델의 효과 측정치가 ground truth로부터 얼마나 떨어져 있는지를 보면, 선형회귀는 비선형적인 부분($X_1$) 을 전혀 캐치하지 못하고 랜덤포레스트는 커브에 노이즈가 많으며 특히 각 피쳐의 극단값으로 갈수록 더 노이즈가 심해짐 (PDP를 봐도 딱히 의미가 없을 것)

💡 제안:

  • 충분한 모델의 성능 평가가 이루어지고 나서(일반화 능력이 보장되고 나서) IML을 적용하기


3. 해석이 필요한 모델을 굳이?

해석 가능한 단순한 모델로도 충분한데 굳이 불투명하고 복잡한 모델을 쓰는 것은 경계해야 합니다. 명백한 성능상 혹은 다른 이점이 있는 게 아니라면, 복잡한 모델 쓰고 IML 분석을 별도로 하느니 그냥 해석 가능한 모델을 쓰는 게 맞죠. 너무 당연한 말이지만 실제로 모델을 적용할 때는 놓칠 수도 있는 부분입니다. 어쨌든 다들 멋진 걸 좋아하니까요.

💡 제안:

  • 트리 모델이나 선형 회귀 같은 단순한 모델들에게 한번 기회를 주기
  • Generalized Additive Models (GAM)처럼 간단한 선형모델과 보다 복잡한 ML 모델 사이의 점진적인 전환이 가능한 선택지도 추천
    • 상호작용 효과가 마스킹될 위험 없이 비선형적인 효과를 모델링할 수 있는 장점


4. 무시할 수 없는 피쳐 간 상관관계

잘못된 외삽

피쳐들이 서로 의존적일 경우, PFI, PDF, SHAP처럼 피쳐들을 섞거나 변화시키는 perturbation 기반의 방법들은 학습 데이터가 아주 적거나 없었던 영역에서 외삽(extrapolation)을 하게 되는데, 이 경우 잘못된 해석으로 이어질 수 있습니다. perturbation 기반 방법들은 조금씩 입력 데이터포인트를 바꿔가면서 모델 예측을 관찰하고, 이걸 집계해서 global한 해석을 만드는데요. 이때 이 가상의 데이터 포인트들은 균등한 그리드에서 추출되거나, 랜덤하게 (sub)샘플링되거나, 퀀타일을 기반으로 뽑기도 합니다. 우선 피쳐가 서로 의존적일수록 이러한 모든 방법들은 전부 비현실적인(실제로는 데이터가 거의 존재하지 않는 구간에서) 데이터포인트들 뽑게 됩니다. 피쳐가 독립적이더라도, 균등한 그리드에서 추출하면 역시 비현실적입니다.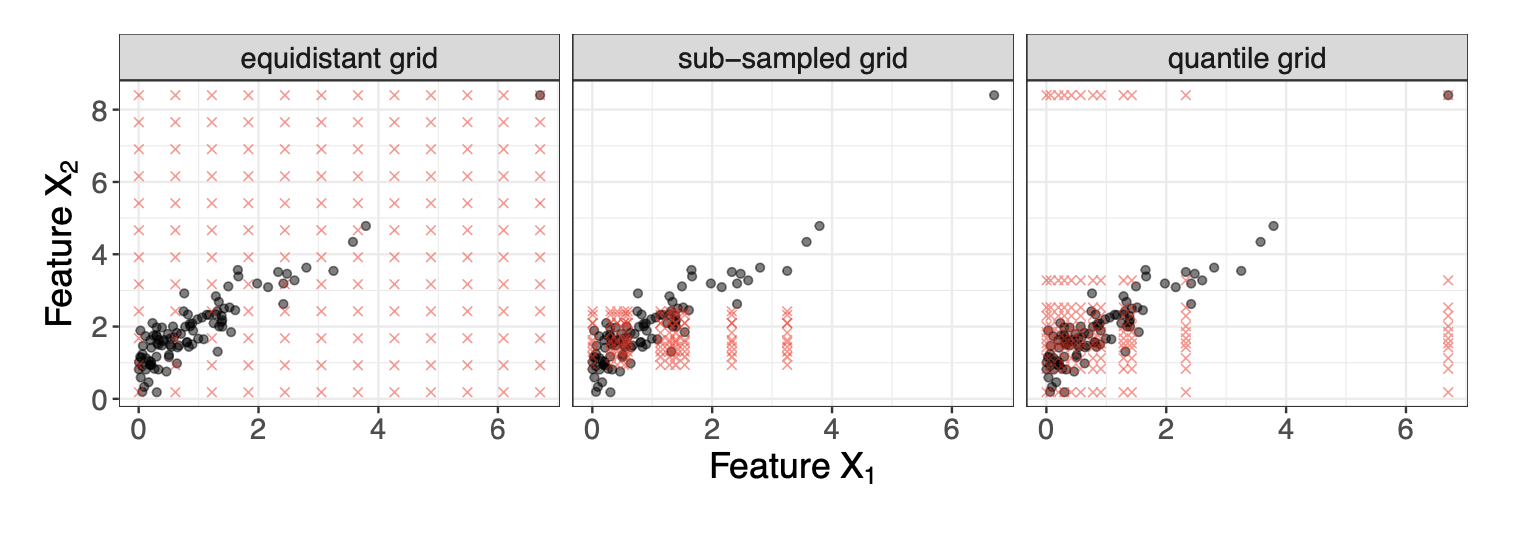

  • 까만점이 실제 데이터 포인트들이고 빨간점이 IML에서 사용하는 가상의 데이터포인트
  • 특히 왜도가 심하고 아웃라이어가 있다면, 균등한 그리드 방식(첫번째 그림)은 아웃라이어와 정상 데이터 사이 영역에서 많이 추출을 하게 됨

따라서 IML 하기 전에 기술통계나 의존도를 측정하는 메트릭을 사용해서 피쳐 간 상관을 확인해야 합니다. 이런 피쳐들을 아예 모델에서 빼기는 어려울 수도 있으므로, 이 상관관계의 구조나 강도에 다른 추가 정보를 제공해야 할 수도 있겠죠.

💡 제안:

  • Perturbation 시 균등분포 추출보다는 섭샘플링, 퀀타일 등의 방법을 사용하기
    • IM 들이 보통 균등분포 추출을 많이 사용하지만 일부는 사용자가 정의한 값을 사용하기를 허용하기도 함
  • Accumulated Local Effect plots (ALE)
    • PDP 대비 서로 상관관계가 있는 피쳐들을 볼 때 유용 (단 매우 저차원에서만 적용가능한 한계)


선형 상관계수 측정의 한계

선형 상관을 측정하는 피어슨 상관계수(PCC)는 거의 0이어도 의존적인 피쳐일 수 있습니다. 즉, 두 피쳐가 독립이면 피어슨 상관계수는 0이지만, 그 반대는 보장되지 않습니다.

💡 제안:

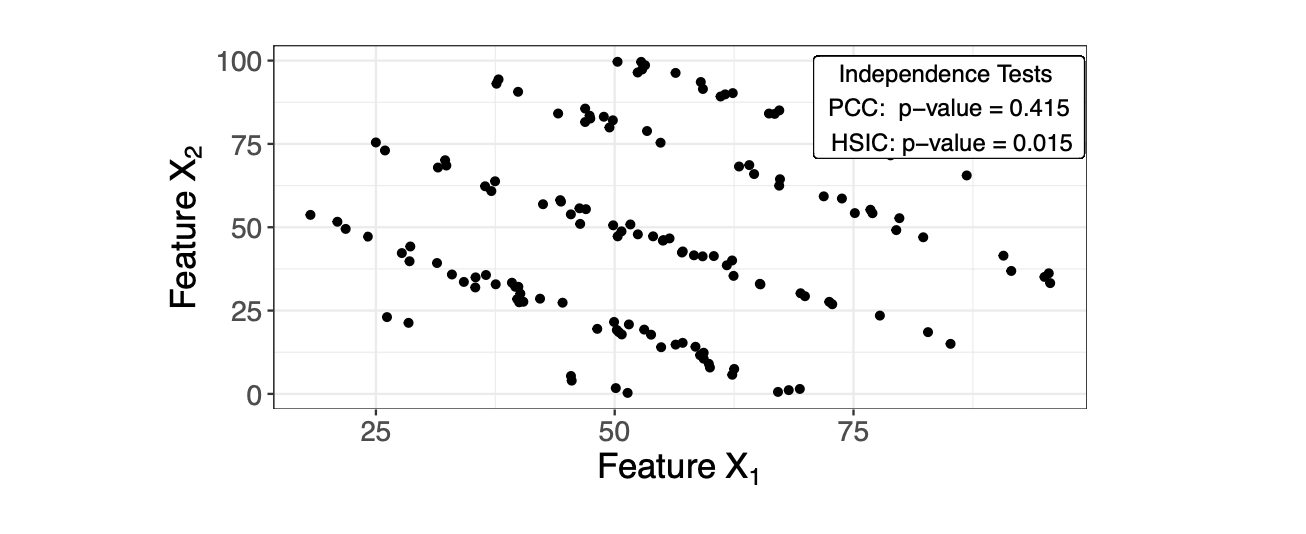의존성이 존재하지만 선형 상관은 0에 가까운 예시. 이 경우 HSIC는 PCC와 달리 0.05 수준에서 유의하게 두 피쳐의 상관을 보여주고 있음


5. 상호작용 효과의 함정

평균을 믿지 않기

PDP나 ALE plot은 예측에 대한 피쳐의 효과를 평균내서 시각화합니다. 만약 피쳐가 상호작용할 경우, 이렇게 평균내는 방식은 위험할 수 있습니다.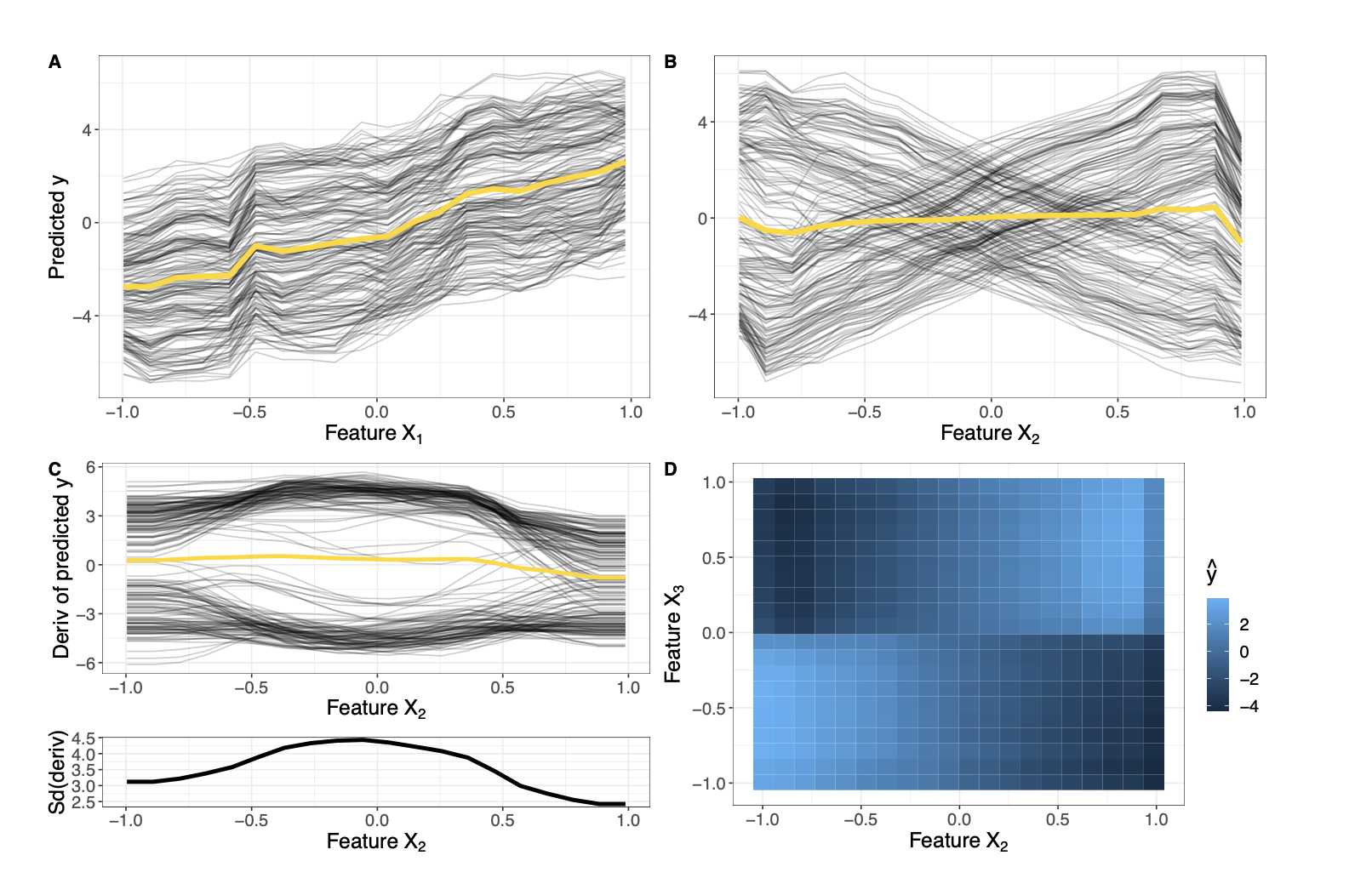

  • 실제 데이터의 관계 $Y = 3X_1 - 6X_2 +12X_2 \mathbb{I} _{X_3>=0}$
    • 즉 $X_3$이 0 이상이면 $+6X_2$, 0미만이면 -$18X_2$가 되는 것 (상호작용 효과가 존재)
  • A,B 그림을 보면 $X_1$과 $X_2$의 marginal 효과를 볼 수 있는데, $X_1$의 경우 큰 문제가 없지만 $X_2$는 $X_3$과의 상호작용 때문에 평균을 내버리면 그 효과가 전혀 드러나지 않게 됨

💡 제안:

  • PDP의 경우, ICE curve를 같이 보기
    • ICE는 각 예측의 이질성을 직접적으로 보여주기 때문
    • A에서는 ICE curve가 다 같은 경향성을 나타내고있으므로 평균 낸 노란색 선과 어긋나는 부분이 없지만 B에서는 노란색 선이 잘 나타내지 못하는 걸 ICE curve가 보여주고 있음
  • 각 피쳐가 다른 절편 값에서 시작하는 경우 derivative 또는 centered ICE curve를 사용하여 절편의 영향도를 날리고 상호작용으로 인한 차이만 볼 수 있기
    • C를 보면, $X_2$가 0 값에 가까워질수록 다른 피쳐 값에 크게 영향을 받는다는 걸 알 수 있음
    • 다만 상호작용이 있다는 것만 알고 그 양상을 알기는 어려운데, 이럴 경우 D처럼 2차원 PDP, ALE plot을 그려서 $X_2$가 $X_3$ 값에 의존하는 것을 확인


주 효과와 상호작용 효과 구분하기

대부분의 IML은 주효과와 상호작용 효과를 잘 분리하지 못합니다. 예를 들어 PFI는 피쳐의 중요도와 그외 모든 다른 피쳐들과의 상호작용 효과의 중요도를 다 합친 값이고, LIME이나 SHAP처럼 각각의 예측에 대한 값을 반환하는 local 한 방법론도 마찬가지입니다.

💡 제안:

  • 주효과와 상호작용 효과를 구분할 수 있는 방법론 사용하기
    • Functional ANOVA
      • 결합분포를 분해해서 주효과와 상호작용 효과로 나누는 방법
    • H-Statistic
      • 두 개의 피쳐나 한개와 나머지 피쳐의 상호작용의 강도를 계산하는 통계치 (2차원 PDP를 단변량 요소로 분해)
    • 다만 둘 다 계산비용은 꽤 되는 편


6. 모델도 IML도 불확실한 변수일 뿐

일반적으로 IML은 평균 추정치만 제공하고, 각 추정치의 불확실성은 계량화하지 않습니다. 문제는 학습된 모델에도 불확실성이 있고(랜덤한 일부 데이터를 기반으로 학습), 계산된 해석에도 불확실성이 있다는 것입니다(예컨대 Shapley value는 연산량 때문에 몬테카를로 샘플링으로 값을 추정). 이런 두 가지 불확실성을 고려하지 않으면 노이즈가 많고 강건하지 않은 결과를 얻을 수 있습니다. 진짜 효과는 없는데 그냥 우연히 값이 크게 나온다든지요. 특히 작은 데이터셋에서 이런 일이 벌어질 가능성이 높고, 우연히 나온 효과는 여러 모델 핏에 대해 평균 내면 없어질 수도 있습니다.

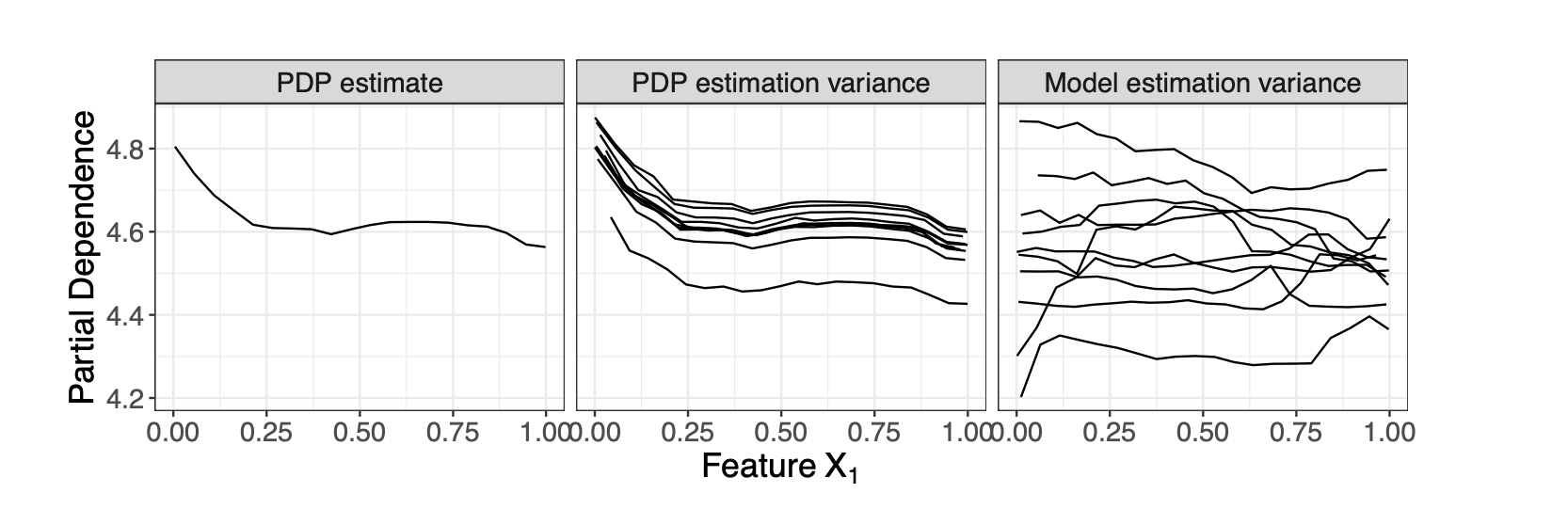하나의 PDP 플랏만 보면 어? 하는데, 두번째 그림을 보면 PDP 추정의 변동이 상당히 크다는 걸 알 수 있고, 세번째 그림을 보면 여러 모델 핏에 따라서는 완전 산발적인 결과가 나온다는 걸 알 수 있습니다. 특히 우리가 알고 싶은 게 딱 지금 학습된 이 특정 모델이 아니라 진짜 X와 Y라면, 모델의 variance도 반드시 고려해야 합니다.

💡 제안:

  • IML 값을 계산할 때 서로 다른 permutation이나 bootstrap sample을 가지고 여러 번 계산하기 (신뢰구간처럼 불확실성 추정 수단을 확보하기 만들기)
  • 여러 model fit에 대해 계산해서 안정성 테스트하기


7. 차원의 저주

인간의 해석 문제

IML을 고차원 데이터셋에 무지성으로 적용(피쳐 효과 시각화하기, 피쳐단위의 중요도 점수 계산하기)해버리면, 결국 매우 고차원의 IML 결과가 나오는데 그걸 보고 인간의 눈으로 직관적으로 해석하기란 거의 불가능합니다. 특히 시각화에 의지하는 방법론일 경우 더더욱 무엇이 중요한지 파악하거나 의미 있는 인사이트를 얻기가 어렵죠.

💡 제안:

  • IML를 적용하기 전에 차원을 축소하기
  • 원래 피쳐를 보존하면서 해석하고 싶다면
    • Feature Selection 기법을 사용하기 (Wrapper, LASSo, component-wise boosting)
    • 만약 피쳐들이 데이터 또는 도메인 지식을 기반으로 의미 있게 그룹핑이 될 수 있다면, 각 피쳐들이 아니라 피쳐 그룹에 대해 IML을 적용하는 것도 방법 (더 효율적이고 적합한 해석을 얻을 수 있음)

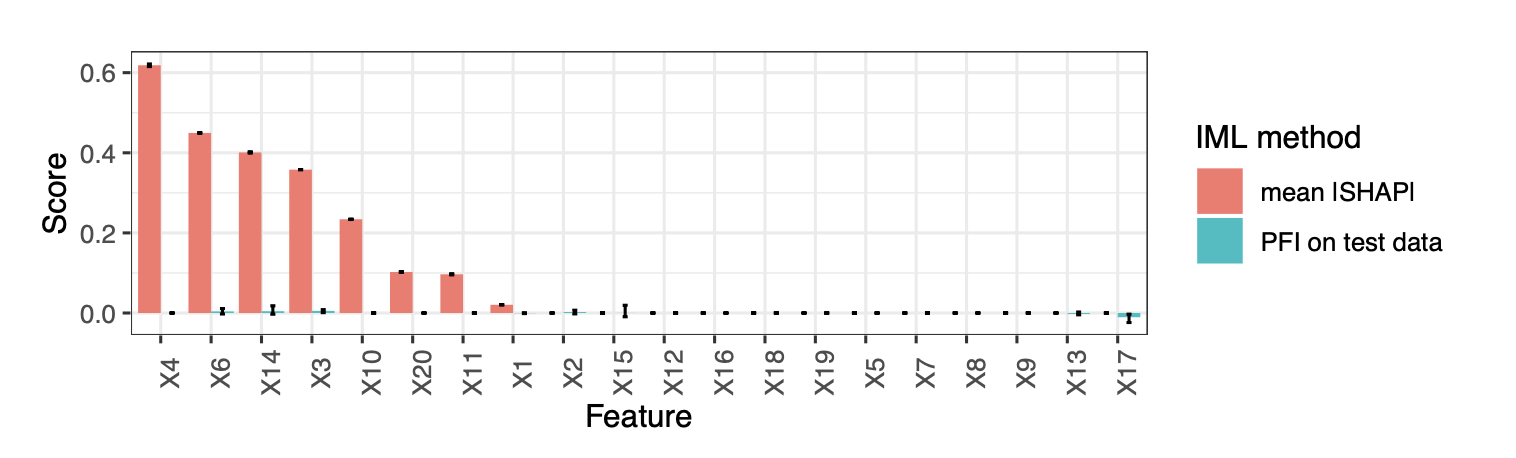
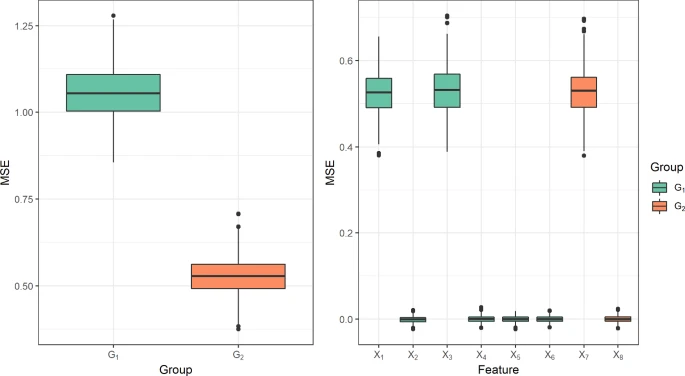이 연구에서는 총 1821개의 피쳐를 행동별 카테고리로 피쳐들을 묶어서 해석을 진행했음 (좌: 피쳐 그룹 단위, 우: 피쳐 단위)


계산 비용 문제

일부 IML은 피쳐 수가 증가함에 따라 계산 스케일이 선형적으로 증가하지 않고 지수적으로 증가합니다. 정확한 Shapley 값을 계산하거나 모든 주효과+상호작용 효과에 대해 full functional ANOVA 를 돌리는 경우가 그렇죠. 계산 비용도 사실 실 사용에서는 가장 강력한 문제 중 하나일 것입니다.

💡 제안:

  • Functional ANOVA의 경우, 주효과와 선택된 2-way 상호작용에 한정해서 보기
    • 선택하는 방법은 H-statistic 같은거 쓰면 되는데 이것도 계산비용이 있긴 함
    • 상호작용 효과는 보통 상호작용 사이즈가 증가하면서 크게 감소하므로, $d-1$-way 상호작용이 유의할 때만 $d$ -way를 보기
  • Shapley 값 기반 방식의 경우, 효과적인 근사법 사용하기(추정치가 수렴할 때까지 랜덤 샘플링, 피쳐 ordering)


다중 비교 문제

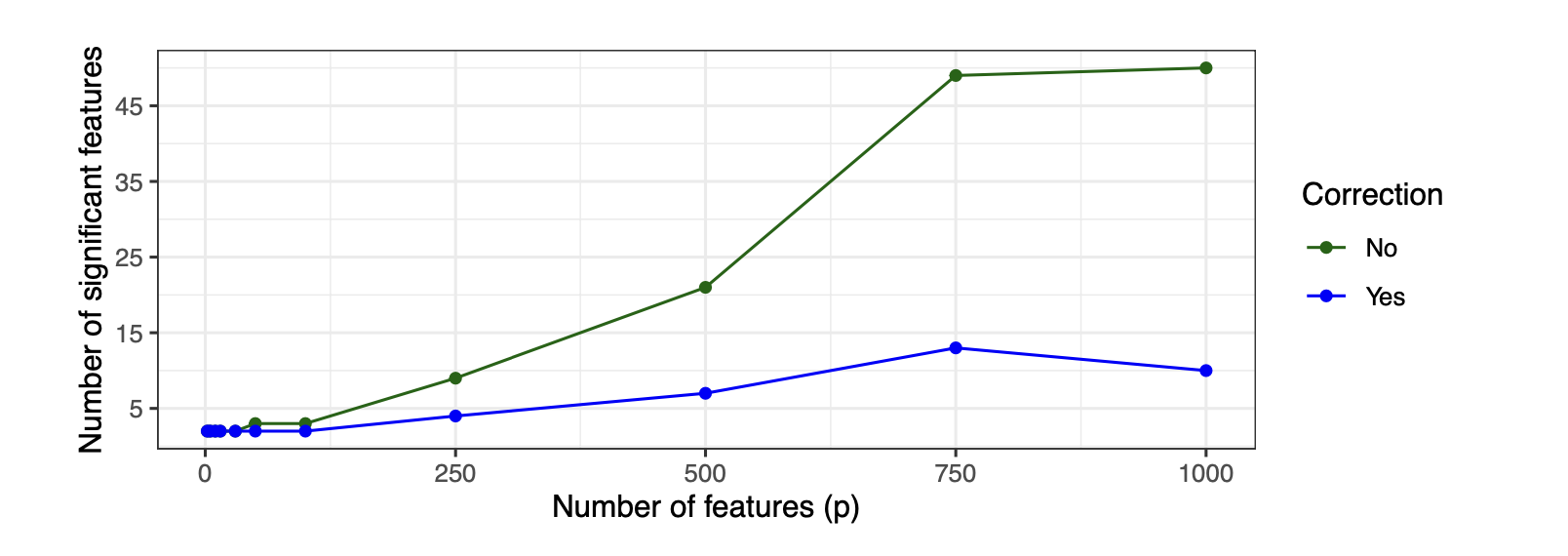
여러 피쳐들의 중요성을 동시에 (가설) 검정하는 것은 1종 오류율을 증가시키는데, 이런 상황은 통계학에서는 Multiple Comparison Problem 이라고 잘 알려져 있습니다. 예를 들어 50개의 피쳐에 대해 $\alpha = 0.05$ 수준에서 유의성 검정을 동시에 한다면(영가설: 이 피쳐가 중요하지 않다) 실제로 모든 피쳐가 중요하지 않은 상황에서, 최소 하나의 피쳐에 대해 영가설을 기각해버릴 확률은 $1-P$(모든 피쳐에 대해 영가설을 기각하지 않음) $= 1- (1-0.05)^{50}$ 로서, 사실 0.9를 넘는 값입니다.

💡 제안:

  • 파란색: Bonferroni correction 적용
  • 초록색: 보정 없음
  • 보정을 하지 않으면 피쳐 개수가 올라갈수록 영가설이 기각되어 유의하다고 판단되는 피쳐의 개수가 같이 올라가는 걸 볼 수 있음


8. 해석은 인과가 아니다

가끔 모델을 해석해서 인과적인 인사이트를 얻고 싶어 하는 경우가 있습니다. 인과적인 인사이트란 원인과 결과, 개입의 효과, 만약 이렇게 하지 않았더라면(counterfactual) 이라는 질문에 대한 대답 등을 모두 포함합니다. 예를 들어 의학 연구자라면 다른 무엇보다도 치료의 효과나 위험성을 알고 싶겠죠. 이 치료를 했을 때 A라는 요인 때문에 성공했다, 만약 안 했다면 사망했을 것이다, 뭐 이런 식의 결론이 유의미한 인사이트처럼 보일 것입니다.

하지만 예측 모델의 인과적 해석이란 사실상 불가능할 때가 많고, 대부분의 해석 방법론은 인과를 말해주지 않습니다. 알려진 표준적인 지도학습 모델들은 피쳐들 간의 상관 관계를 가능할 만큼 활용할 뿐, 인과 관계를 모델링하기 위해 디자인되지 않았습니다.

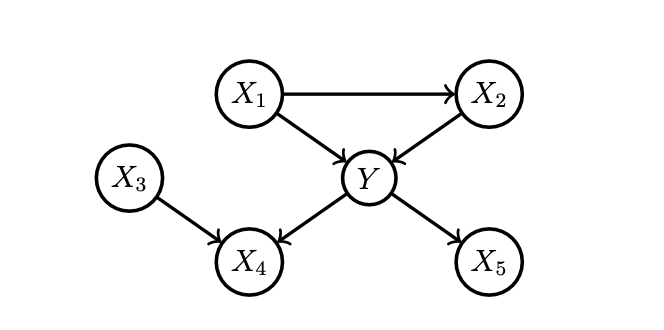예를 들어 이런 구조를 갖는 구조적 인과 모델(SCM; Structural Causal Model) 하에서 데이터를 생성하고, 여기에 선형 모델을 학습시켰다고 합시다. 그러면 뭐 $\hat{y} = 0.33x_1 + 0.32x_2 -0.33x_3 +0.34x_4 + 0.33x_5, R^2 = 0.94$ 이런 식의 결과를 얻고 모든 피쳐들의 회귀계수가 통계적으로 유의할 수도 있습니다. 원래 인과 구조에서는 $X_3$, $X_4$, $X_5$는 $Y$의 원인이 아니지만 그걸 모델이나 IML이 알 도리는 없는 거죠.

💡 제안:

  • 데이터, 모델, IML에 대해 충분한 가정을 만족하는지 확인한 후에 인과적인 해석 하기


Posts, Data
xai
This post is licensed under CC BY 4.0 by the author.