Conformal Prediction으로 모델의 불확실성 계산하기

내 모델의 예측은 얼마나 확실한가

머신러닝 모델을 사용해서 의사결정을 할 때 누구나 할 법한 생각은 이 모델의 판단을 얼마나 믿을 수 있을까? 라는 것입니다.

이런 어려운 문제들에서조차 모델은 “이 사진은 대걸레다”라고 하지 “이 사진은 대걸레일 수도 있고 쉽독일 수도 있다”라고 하는 경우는 없습니다(그러면 사실 의미가 없죠). 기본적으로 특정 값을 정답으로 내놓는 point prediction이기 때문입니다. 얼마나 확실하게 대걸레인 걸까? 에 대한 정보는 잘 제공되지 않지만, 이는 모델의 결과를 어떻게 활용하느냐에 따라 매우 중요한 정보일 수도 있습니다. 마찬가지로 값을 예측하는 모델이 있다면, 모델이 100으로 예측했을 때 그 예측값으로 무엇을 할 수 있는지는 99과 101 사이의 100인 건지 50과 150 사이의 100인 건지에 달려 있을 것입니다.

물론 어떤 모델들은 로지스틱 확률값, 소프트맥스 아웃풋처럼 ‘모델이 생각하는’ 확률을 0과 1 사이의 값으로 알려주기도 합니다. 문제는 그러한 값들은 휴리스틱한 개념으로서의 확률일 뿐이라는 것입니다. 경험적으로 모든 분류 케이스 중에서 10개 중 9개는 맞힌다고 했을 때 90%의 확률이라고 할 수 있지, 모델이 이 케이스에 대해서 90%로 대걸레로 예측했다고 해서 그걸 확률이라고 보기는 어렵다는 것이죠. 극초기의 GPT가 누가 봐도 말도 안 되는 소리를 당당하게 지어내던 게 기억나시나요? 학습된 모델이 자신감 있는 오답을 내놓는 건 아주 흔히 있을 법한 일입니다.

예시를 들자면, 제가 귤 농장 주인이라고 칩시다. 귤을 박스로 판매하고 있는데 기계를 써서 상한 귤을 골라내고 있습니다. 기계의 머릿속에 넣어 줄 모델을 학습시켰는데 정확도가 한 82% 나왔습니다. 성능을 높이면 좋겠지만 아무리 데이터를 늘리고 모델을 바꾸고 파라미터 튜닝을 하고 별 난리 굿을 쳐도 82%가 한계입니다. 각 박스의 95% 이상은 멀쩡한 귤이라고, 즉 상한 귤이 들어갈 확률은 5% 미만이라고 보장할 수 있다면 손님들이 믿고 살 수 있고 안 좋은 리뷰도 달리지 않을 것 같은데 어떻게 해야 할까요? 예측 확률이 95% 이상인 귤만 박스에 넣기는 해결책이 아닐 것입니다.

정말 모델의 불확실성에 대한 답을 얻고 싶다면, 이런 휴리스틱한 개념의 확률(불확실성)을 엄밀한 정의로 바꿔줄 필요가 있습니다. 그 방법론이 바로 오늘 이 글에서 소개한 Conformal Prediction입니다. 등각 예측, 정합 예측 등으로 번역되는 것 같지만 확정적인 한국어 명칭은 없는 것 같아서 이 글에서는 계속 Conformal Prediction이라고 하겠습니다.

Conformal Prediction 하는 법

예를 들어 각 이미지를 $K$ 개의 클래스 중 하나로 분류하는 과제가 주어졌고, 우리 모델은 뭐 아무거나… 신경망 분류기라고 해봅시다. 이 분류기 $\hat{f}$는 각 클래스에 대한 휴리스틱한 확률(예를 들면 softmax 출력값)을 아웃풋으로 돌려주고, 그 값이 가장 높은 클래스를 예측값으로 고릅니다. 즉 4개의 클래스에 대해 [0.6, 0.2, 0.1, 0.1] 이런 softmax score가 나왔다면 0.6인 첫번째 클래스로 예측을 하는 거죠.

Conformal Prediction을 하기 위해서 우리는 $n$개의 새로운 이미지를 가져옵니다. 500개 정도? 모델 학습 과정에서 쓰이지 않았던 이 작은 데이터셋을 $(X_1, Y_1), \cdots, (X_n, Y_n)$ 라 하면, 이 데이터들과 이미 학습된 분류 모델을 사용해서 다음을 만족하는 예측 결과의 집합(prediction set) $\mathcal{C}(X_{test}) \subset {1, \cdots, K}$ 을 만드는 것이 목표입니다.

\[1- \alpha \le P(Y_{test} \in \mathcal{C}(X_{test})) \le 1- \alpha + \frac{1}{n+1}\]

이때 $\alpha$ 는 사용자가 이 정도는 허용하겠다! 라고 정한 0과 1 사이의 오류율입니다. 만약 우리가 고른 $\alpha$ 값이 10%라면, 위 식의 의미는 이 작은 테스트셋에 대해서 실제 라벨인 $Y$가 우리의 예측 결과 집합 $\mathcal{C}$에 포함될 확률이 거의 정확히 90% 정도라는 것입니다. 이를 marginal coverage라고도 하는데, 확률분포에서 x에 대한 주변분포, 주변 확률(marginal probability)은 x에 영향을 주는 다른 변수 y를 다 합해서 계산한다는 사실을 떠올리면 의미가 통할 것입니다. 모든 테스트 셋의 데이터 포인트들 각각에는 랜덤성이 존재하지만 이걸 다 합쳐서 봤을 때 90% 정도의 커버리지가 나온다는 뜻에서 marginal coverage인 것이죠.

예를 들면 모든 이미지에 대해 각각 예측결과를 이렇게 나타낼 수 있습니다. 그냥 point prediction을 했다면 각각 fox squirrel, fox squirrel, marmot 요렇게만 나왔겠지만 conformal prediction의 결과물은 집합입니다. 각 집합은 실제 정답을 포함하고 있을 수도 있고 아닐 수도 있는데, 이걸 포함할 전체 확률이 약 90%가 되게 하자는 것입니다.

그러면 이런 예측 결과 집합들을 어떻게 만들까요?

(1) 모델의 ‘틀림’ 점수를 구하기

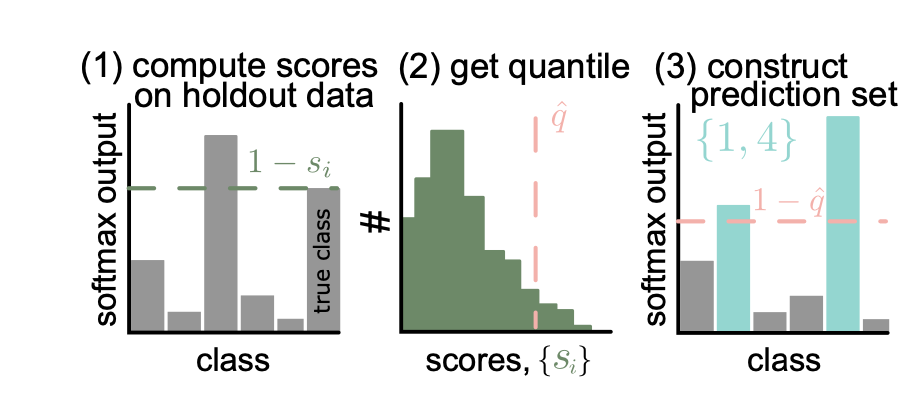
• non-conformity score $s$ 라는 걸 정할 건데, 이 점수는 모델의 예측이 틀릴수록 높아지는 값으로 함 (정하기 나름)
• 우리 예시에서는 (1-정답 클래스의 소프트맥스 스코어) 즉 $s_i = 1- \hat{f}(X_i)_{Y_i}$
• 이 점수를 모든 500개의 새 데이터셋에 대해 구하면, 이 점수의 분포를 알 수 있음

(2) 이 점수의 $1-\alpha$ 퀀타일 $\hat{q}$ 을 구하기

• $\alpha = 0.1$ 이라면, 모델 예측이 틀린 순으로 나열했을 때, 점수가 $\hat{q}$ 정도 되면 상위 10% 정도 되는 선이라는 것
• 즉 전체 분포를 봤을 때 중 10%만 이거보다 더 틀린다는 최소한의 보장

(3) softmax 값이 $1-\hat{q}$ 보다 큰 클래스들을 고르기

• $\mathcal{C}(X_{test}) = { y : \hat{f} (X_{test})_y \ge 1- \hat{q} }$
• 반전을 여러 번 해서 헷갈리는데, 즉 전체 점수 기준으로 10% 안 되는 수준의 softmax 값이 나오는 클래스는 버리고 그 이상인 클래스만 최종 예측 결과 집합으로 쓰겠다는 것

이렇게 만든 $\mathcal{C}$ 는 앞서 언급한 조건(정답을 포함할 확률이 $1-\alpha$ 근처)을 만족하게 됩니다. 증명이 궁금하신 분들은 여기의 Appendix를 보시면 됩니다. $q$를 구한 과정을 다시 생각해보면 정답 softmax 값의 90% 정도가 $1-q$ 이상인 것이기 때문에 어느 정도 직관적으로 이해가 됩니다.

$\mathcal{C}$ 의 특징을 보면, 모델이 불확실할수록 크기가 커지는 집합이라고 할 수 있습니다. 불확실함의 이유는 2가지인데요.

1. 모델 자체가 불확실하다 = 모델이 잘 틀리는 모델이면 모델이 틀리는 정도를 나타내는 $s$의 분포가 오른쪽으로 쏠려서 $1-\alpha$ 퀀타일 값이 더 커지게 되고, $1-\hat{q}$이 작아지게 되므로, 마지막 $\mathcal{C}$를 정하는 임계치가 낮아져서 더 많은 클래스가 예측결과 집합에 속하게 됨.
2. 이미지가 불확실하다 = 이미지 분류에서 이미지 자체가 난이도가 높다면(매우 쉽독같은 대걸레, 매우 대걸레같은 쉽독) 여러 클래스에 비슷하게 높은 휴리스틱 확률값을 주게 되고, 그러면 같은 임계치에 대해서도 여러 클래스가 그 임계치를 통과할 수 있음.

이처럼 Conformal Prediction을 통해 실제로 모델의 불확실성을 반영한 예측 집합 또는 예측 범위를 결과물로 얻을 수 있으며, ‘정답을 맞힐 확률이 특정 값(예를 들면 95%) 이상인’ 결과물을 보장받을 수 있습니다. 이 방식의 장점은 여러가지인데 첫번째는 어떤 가정에 의해서 확률을 계산하는 게 아니라 데이터의 분포에 대한 가정이 필요 없고, 이미 학습이 완료된 모델과 새로운 작은 데이터셋만 있으면 적용 가능하다는 점입니다.

무엇보다 모델에 종속적이지 않기 때문에 어떤 예측 모델에도 똑같은 방식을 거치면 됩니다. 우리의 예시에서 사용한 softmax 점수처럼 각 모델의 불확실성을 나타낼 수 있는 대략적인 개념이 있다면 이를 위와 같은 과정을 거쳐서 엄밀한 수준의 정량화된 불확실성으로 바꿔 줄 수 있습니다. 물론 그 $s$는 모델의 틀린 정도를 줄세울 수 있는 개념이어야 하며, 점수를 잘못 정의하면 그 결과물인 $\mathcal{C}$ 도 무용해지겠지만요.

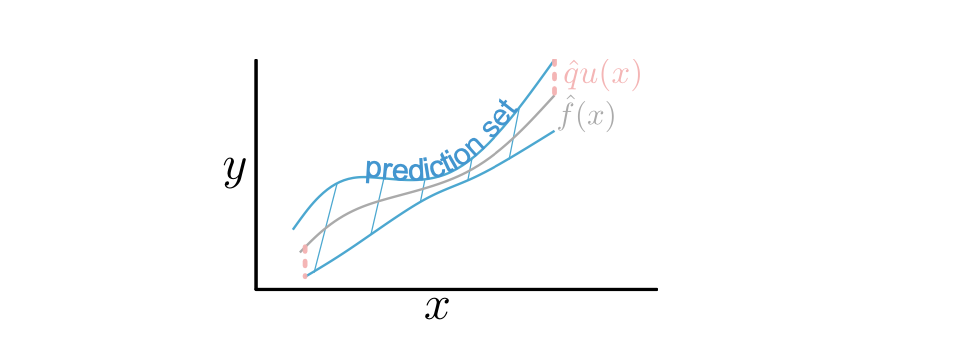
모델에 종속적이지 않기 때문에 분류가 아닌 회귀 문제에서도 비슷한 접근을 해볼 수 있습니다. 이 경우 Conformal Prediction의 결과물은 사실상 클래스의 집합이 아닌 어떤 예측 구간(prediction interval)이 되겠죠.

어떤 함수 $u(x)$가 있어서 데이터의 불확실성이 커질수록 커지는 결과(스칼라값)를 돌려준다고 칩시다. 데이터의 가우시안 분포에 대한 가정이 들어간다면 표준편차 $\hat{\sigma}(x)$일 수도 있고, 모델을 앙상블 시켰을 때나 아니면 모델의 일부를 드롭아웃 시켰을 때 발생하는 결과의 변동성을 이 값으로 사용할 수도 있습니다. 아무 가정 없이 조금 더 일반화된 방식을 생각해본다면, 이미 학습된 회귀 모델의 잔차를 학습하는 추가적인 모델을 학습시켜서 그 값을 쓸 수도 있습니다. 어쨌든 point predictin $\hat{f}(x)$ 이 있고 이러한 불확실성 점수 $u(x)$ 가 있다면, 다음과 같이 non-conformity score를 정의해볼 수 있습니다.

\[s(x,y) = \frac{\vert y- \hat{f}(x) \vert}{u(x)}\]

그 뒤로는 똑같습니다. $s$의 $1-\alpha$ 퀀타일 $\hat{q}$ 을 구하게 되면,

\[P(X_{\text{test}}, Y_{\text{test}}) \le \hat{q}) \ge 1- \alpha \Longrightarrow P(\vert Y_{\text{test}} - \hat{f}(X_{\text{test}})\vert \le u(X_{\text{test}})\hat{q}) \ge 1-\alpha\]

따라서 다음과 같이 예측 구간 $\mathcal{C}$ 이 구해집니다.

\[\mathcal{C}(x) = \left[ \hat{f}(x) - u(x)\hat{q}, \hat{f}(x) + u(x)\hat{q} \right]\]

참고한 글

• Week #1: Getting Started With Conformal Prediction For Classification
• A Gentle Introduction to Conformal Prediction and Distribution-Free Uncertainty Quantification
• Theoretical Description for Conformity Scores