왜 딥러닝은 정형 데이터에 잘 안 통할까

Why do tree-based models still outperform deep learning on typical tabular data? (2022) 를 읽어보았습니다.

오늘은 각종 딥러닝 모델이 정형 데이터에서 결정 트리 기반의 앙상블 모델(이하 트리 모델)에 비해 성능이 떨어지는 현상을 분석하고 3가지 발견을 가능한 원인으로 제시한 논문을 읽어보겠습니다. 자세한 내용으로 들어가기 전에, (이전에 비슷한 연구들이 많이 나왔긴 했지만) 정형 데이터에 대해 정말로 딥러닝 모델이 잘 못하나? 를 먼저 짚고 넘어가긴 해야겠죠.

• 비교한 트리 모델: Random Forest, XGBoost, Gradient Boosting Tree
• 비교한 딥러닝 모델: MLP, Resnet, FT-Transformer(Feature Tokenizer Transformer), SAINT(Self-Attention and Intersample Attention Transformer)
• 사용한 정형 데이터셋의 조건: 칼럼끼리 이질적임(서로 결이 다른 데이터임), 현실(real-world) 데이터임, 너무 고차원이 아님, 너무 작지 않음, 시계열/스트리밍이 아님, 너무 쉽지 않음(그냥 로짓회귀 때려서 성능 잘 나오면 뺌) 등
  • 사실 이 논문은 벤치마크로 사용할 만한 45종의 정형 데이터셋의 제공도 contribution이다 라고 하고 있지만 사실 궁금한 건 왜 딥러닝이 못하는데? 에 대한 대답이므로 데이터셋에 대한 상세 내용은 패스함

수치형 변수만 사용한 데이터에 대한 실험

수치형 변수와 명목형 변수를 모두 사용한 데이터에 대한 실험

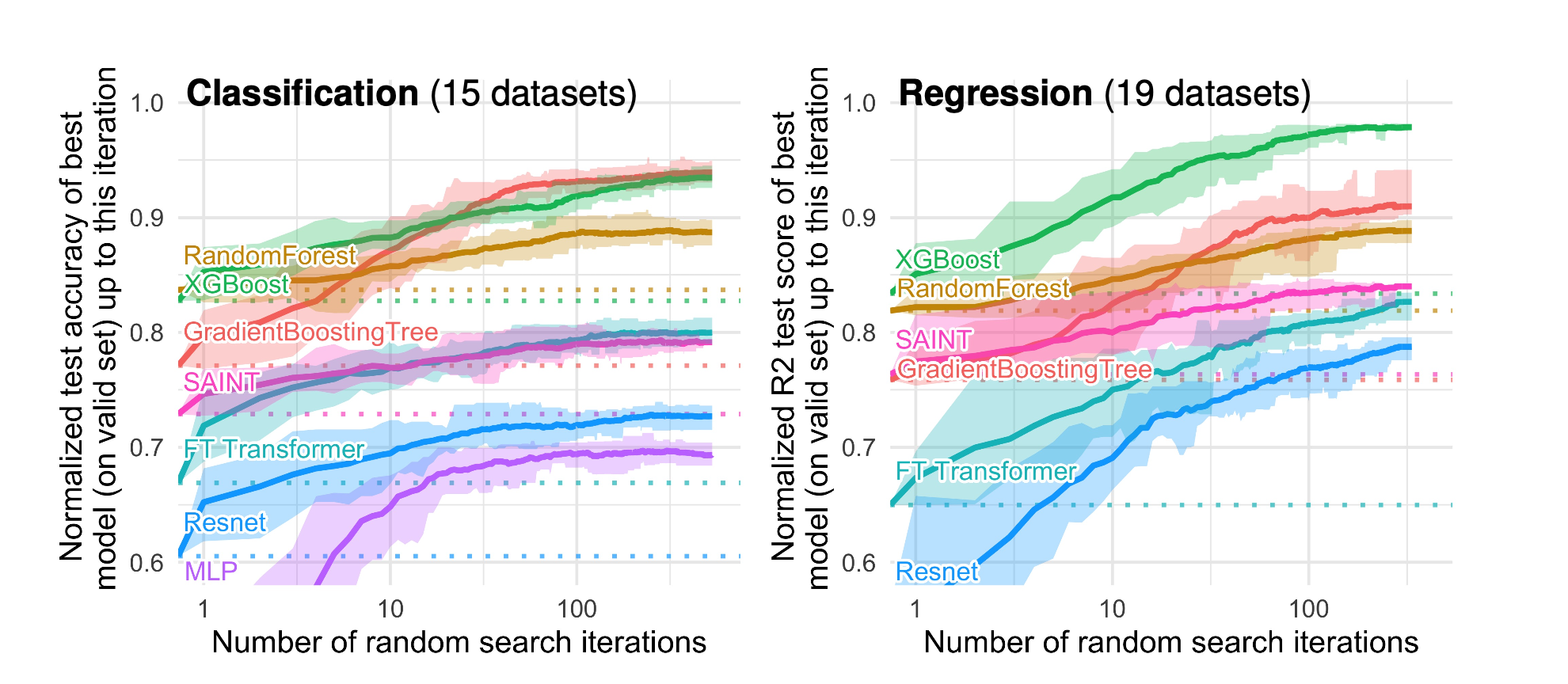
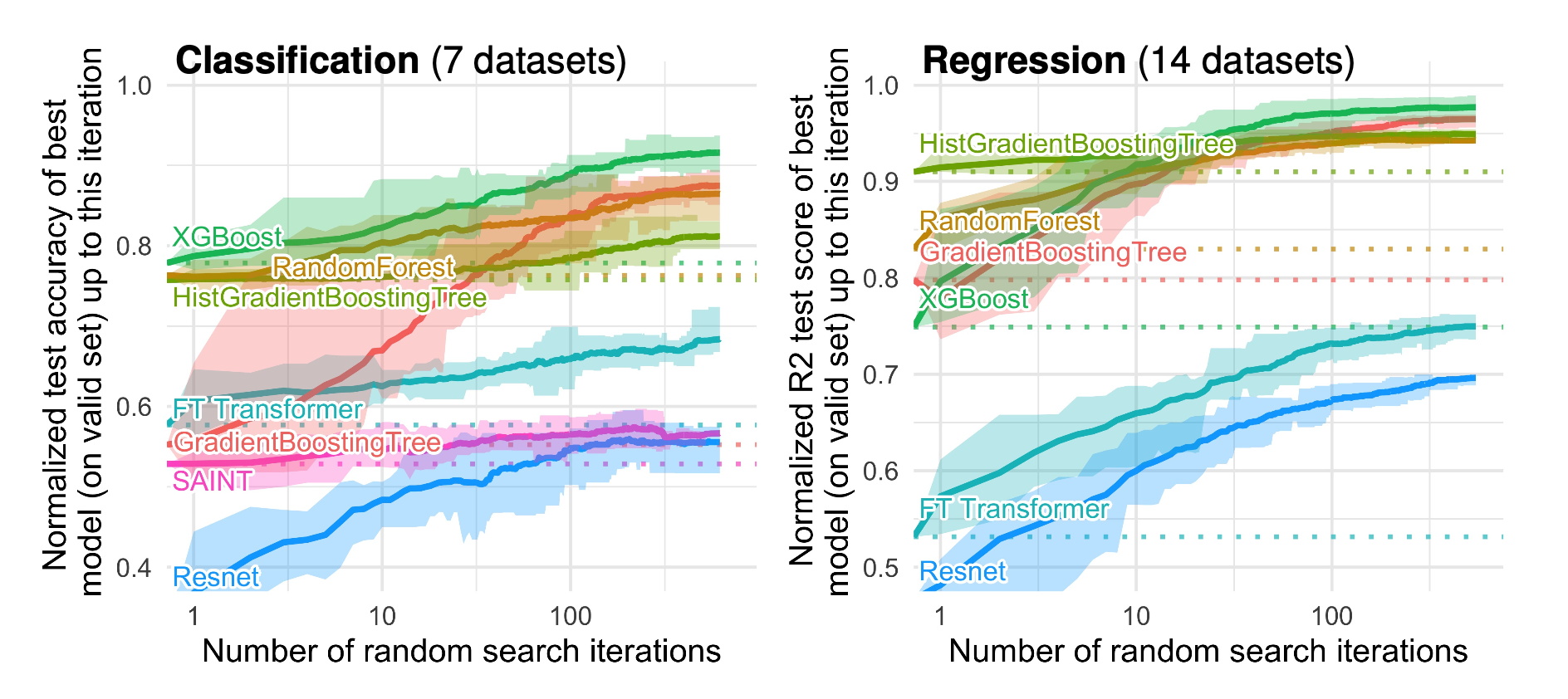
위 그림들은 여러 벤치마크 정형 데이터에 대해 트리 모델과 딥러닝 모델의 차이를 보여줍니다. x축은 하이퍼파라미터에 대한 랜덤 서치 iteration 횟수이며, 분류과제의 경우 정확도, 회귀과제의 경우 r2를 성능 지표로 사용했습니다. 정형 데이터를 위해 개발된 트랜스포머 모델들조차도 전반적으로 떨어지는 성능을 보이고 있죠. 그 외에도 그림에서 알 수 있는 사실은 크게 2가지입니다.

• 하이퍼파라미터 튜닝을 아무리 많이 해도 딥러닝이 더 잘하지 못함. 모든 랜덤 서치 iteration 단계에 대해서 트리 모델이 더 잘했고, iteration이 계속 커져도 성능 갭이 유지되는 걸 볼 수 있음 (심지어 서치에 걸리는 시간은 보통 딥러닝이 더 오래 걸린다는 사실까지 고려하면…😟 )
• 보통 정형 데이터의 카테고리컬한 피쳐 때문에 딥러닝이 잘 못한다고들 하는데, 위 실험 결과를 보면 수치형 변수만 사용한 경우에도 둘 다 사용한 경우와 동일하게 항상 트리 모델이 우월했음

이제 논문은 그럼 대체 왜 그럴까? 에 대한 답을 찾으러 갑니다.

여기서 모델의 inductive bias라는 개념이 등장합니다. 머신러닝 모델에서 inductive bias란, 모델이 학습하는 데이터에 대해 가지는 어떤 가정을 의미합니다. 어떤 모델인지에 따라 가정의 방향이나 강도는 다를 수 있습니다. 선형 회귀는 선형 회귀의 가정을 가지고 있을 것이고, CNN은 CNN의 가정을 가지고 있겠죠. 특히 딥러닝 모델은 시계열이나 비전, 자연어 등 각 도메인에서 좋은 성능을 내도록 아키텍쳐가 발전해왔기 때문에 당연히 각각의 데이터에 적합한 편향이 존재할 것이라고 생각해볼 수 있습니다. 앞의 단어가 뒤의 단어와 의미적으로 연관이 있을 거라든지, 이미지에서 가까이 있는 것들끼리 주는 지역적인 정보가 있다든지 하는 가정들이 바로 널리 알려진 딥러닝 모델들의 기본적인 핵심 가정입니다. 이 연구는 이처럼 딥러닝 모델이 가지고 있는 가정들의 어떤 부분이 정형 데이터에 적합하지 않은지를 밝히고자 몇 가지의 실험을 진행했습니다.

1. 정형 데이터는 smooth한 경계선을 가지고 있지 않음

첫번째 실험은 학습 데이터의 타겟 변수를 가우시안 커널을 이용해서 smoothing을 시키는 것입니다. 이때 커널의 length scale을 다르게 해서 모델들의 성능에 어떤 영향을 미치는지 봅니다.

smoothing 정도에 따른 모델들의 테스트 성능 변화

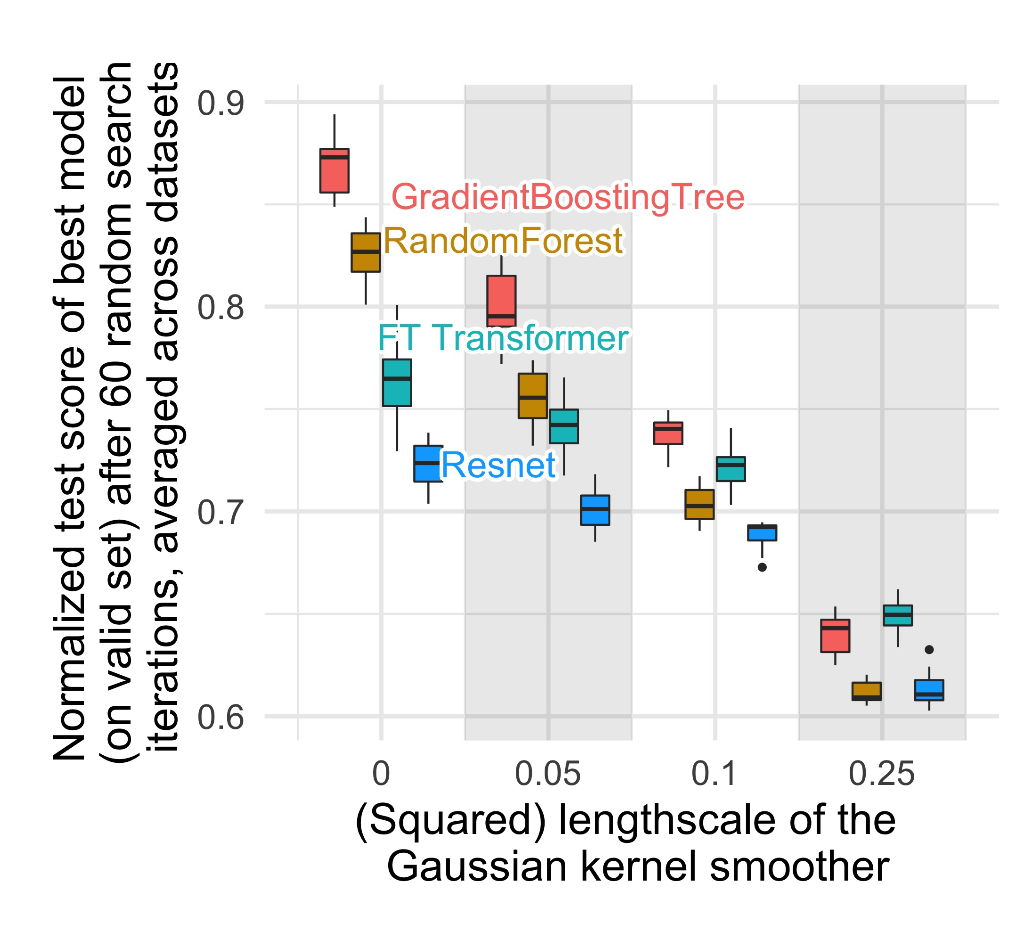
length scale이 커진다는 것은 학습 시 target function이 더 smooth해진다는 것이고, 데이터의 불규칙한 패턴들을 말 그대로 깎아낸다는 뜻입니다.

그림의 가장 좌측의 length scale이 0인 구간은 smoothing을 안 한, 원본 데이터를 그대로 사용한 결과인데요. 두 개의 트리 모델이 두 개의 딥러닝 모델보다 성능이 훨씬 좋은 상태에서 시작하죠. 작은 length scale 로 smoothing이 들어간 두번째 구간을 이 구간과 비교해봅시다. RF랑 GBT의 성능이 뚝 떨어진 것과, FT Transformer와 Resnet의 성능은 거의 똑같이 유지된 것을 볼 수 있습니다. 그 전에도 이미 알아서 smooth solution으로 학습을 하고 있었던 겁니다. 그리고 우측으로 더 갈수록(smoothing scale이 커질수록) 모든 모델의 성능은 다 비슷해지며, 매우 낮은 수준으로 내려가죠.

이 결과가 알려주는 사실은 정형 데이터의 target function은 원래 smooth하지 않은데(인위적으로 smooth하게 만들어버리면 성능 감소), 문제는 딥러닝은 smooth한 경계선을 학습하는 방향으로 편향되어 있다는 것입니다.

x,y축: 학습 데이터의 x,y 피쳐

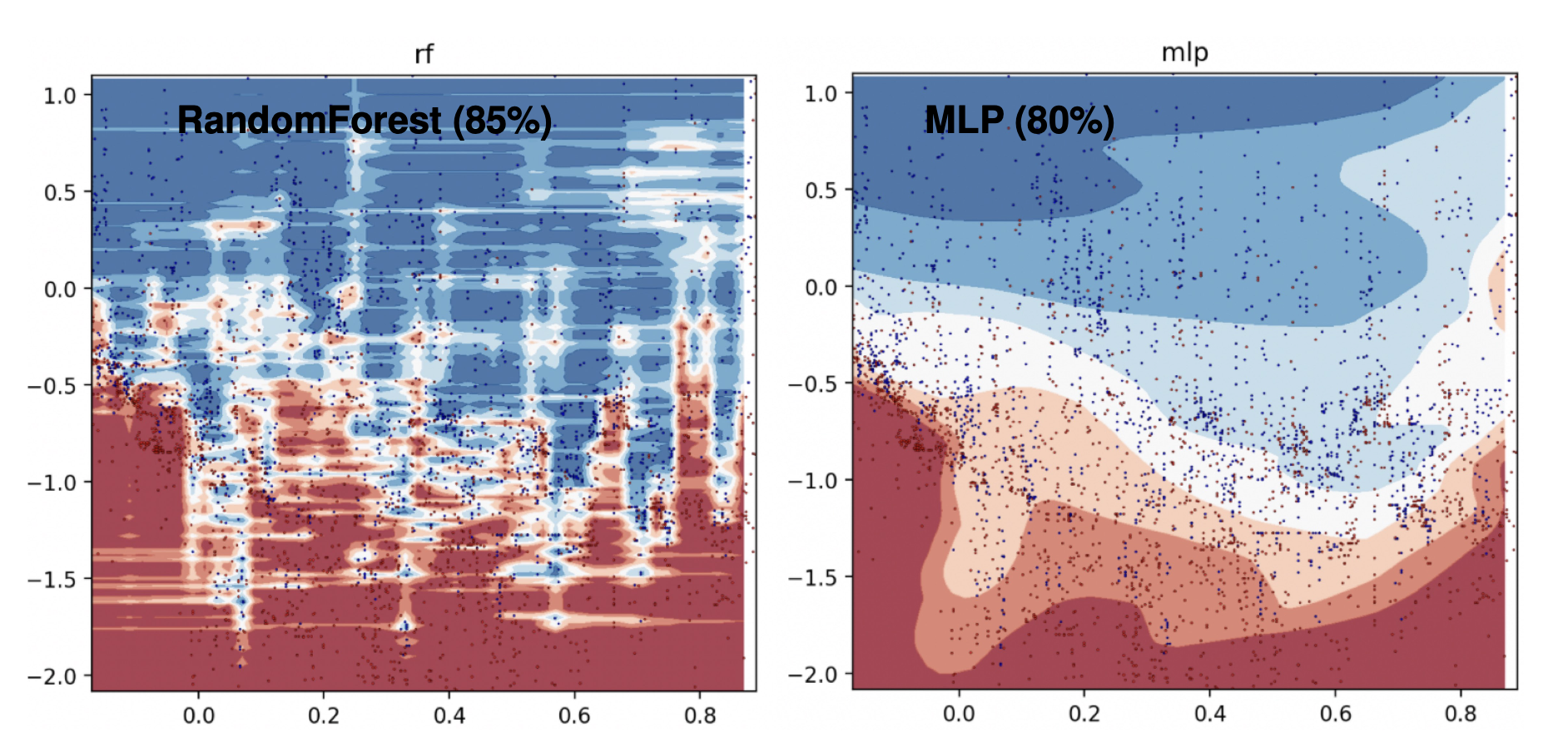
이 그림을 보면 더 잘 이해가 됩니다. 우측의 MLP는 학습 경계선을 매우 부드럽게 만들어버리는데, 좌측의 Random Forest는 데이터의 불규칙하게 튀는 부분을 깎지 않고 그대로 유지하는 것을 볼 수 있습니다.

2. 정형 데이터에는 쓸모없는 피쳐가 많음

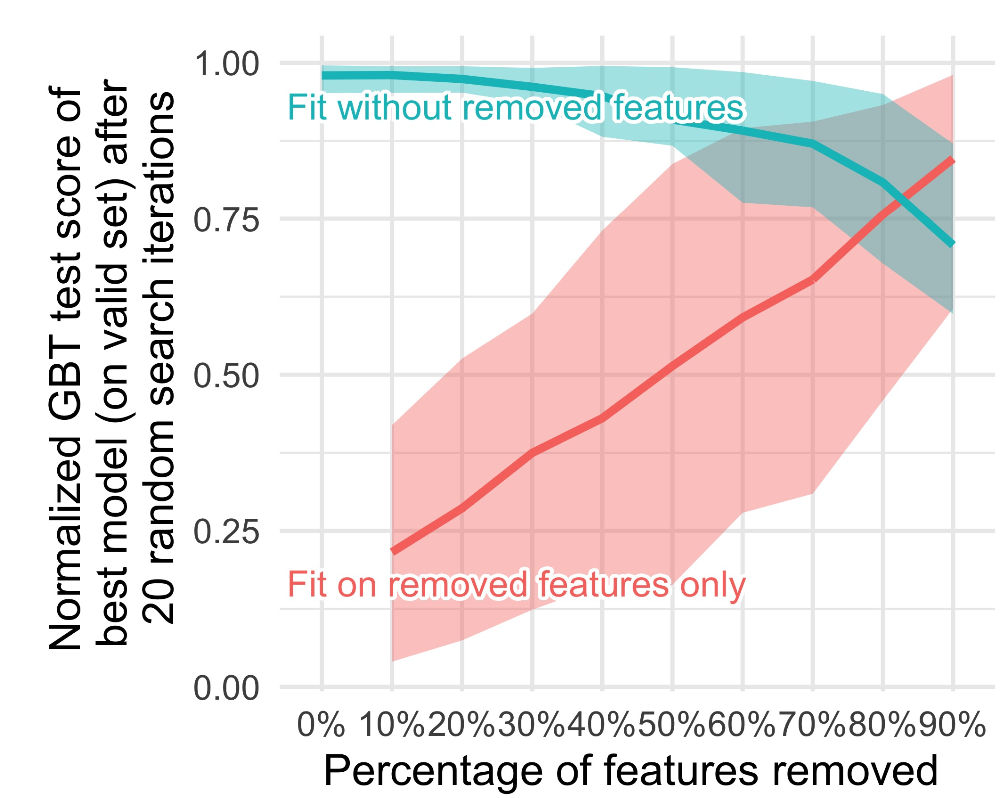
위 그림은 Random Forest를 통해 피쳐 중요도를 계산하고, 중요도가 낮은 피쳐를 차례대로 제거하거나(파란 선) 중요도가 낮은 피쳐부터 사용하여 학습하였을 때(빨간 선) GBT의 테스트 성능 변화를 그린 것입니다.

정형 데이터는 보통 굉장히 다른 결의 정보를 지닌 칼럼들로 구성되어 있는 경우가 많고 그 중 상당수는 타겟 변수 예측에 별로 도움이 되지 않는 uninformative한 피쳐입니다. 빨간 선을 보면 피쳐 중요도가 낮은 순서로 50% 정도만 사용했을 때 모델의 성능은 처참하죠. 정말 쓰잘데기 없는 피쳐들이 있구나 라는 걸 알 수 있습니다. 이어서 파란 선을 보면, 모든 피쳐를 다 사용했을 때 대비 피쳐 중요도가 낮은 순서로 50% 정도까지 없앴을 때 모델의 성능이 많이 떨어지진 않았네요. 즉 전체 데이터의 절반 정도의 피쳐가 쓸모없다고 치면 GBT는 그걸 넣고 돌리나 안 넣고 돌리나 별로 영향을 안 받는다는 겁니다.

이번엔 두 개의 트리 모델과 두 개의 딥러닝 모델을 비교합니다.

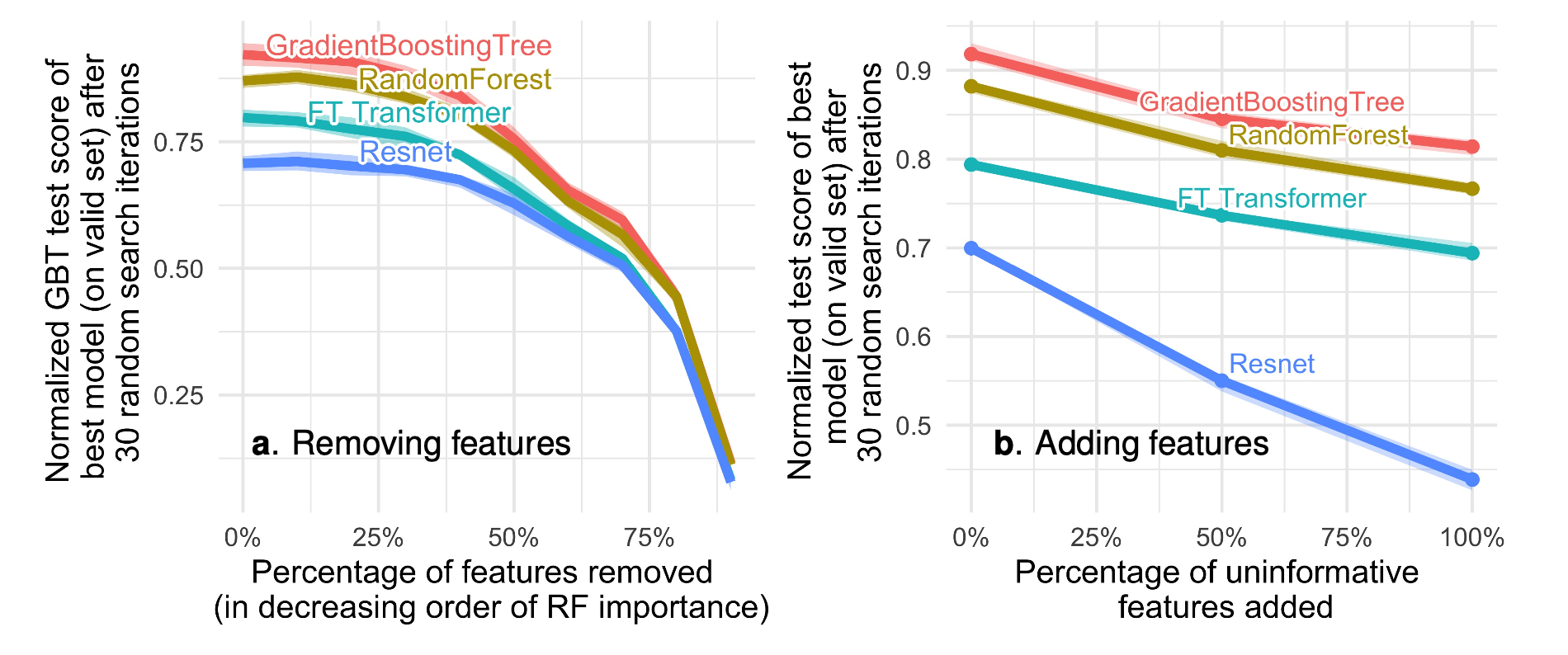
우선 우측 그림을 보면, 타겟 변수와 명백히 관련이 없는 피쳐를 무작위로 만들어서 계속 추가할 때, 특히 Resnet의 성능이 뚜렷하게 감소하면서 굉장히 격차가 커지는 걸 볼 수 있습니다. 기본적으로 MLP는 uninformative한 피쳐에 강건하지 않은데, 정형 데이터에는 보통 그런 피쳐가 많다는 게 문제가 아닐까 라는 문제제기죠.

반면 좌측 그림을 보면 (오타가 좀 있는 것 같습니다. GBT test score → test score, decreasing → increasing) 이번에도 Random Forest의 피쳐 중요도를 기반으로 중요하지 않은 피쳐들을 더 많이 제거하는데, 제거할수록 모델들의 성능 갭이 줄어드는 것을 볼 수 있습니다. 제거 비율이 많이 증가하면 사실상 중요한 피쳐들도 잘리게 되는데, Resnet 입장에서는 중요한 피쳐도 없어지지만 안 중요한 피쳐가 제거됨으로써 그 효과가 어느 정도 상쇄되어 다른 모델들과 고만고만해진다는 해석을 하고 있습니다.

3. 정형 데이터는 rotation 하면 안 됨

딥러닝 모델은 비교적으로 rotationally invariant(즉 데이터의 rotation 시 모델 아웃풋 변화가 없음, 이하 RI)하게 학습하도록 설계되어 있습니다. 예를 들어 이미지 데이터를 학습할 경우, 모델의 과제는 전반적인 모양을 배우는 것이므로 다른 축으로 이미지를 회전시키더라도 똑같이 알아볼 수 있어야 합니다.

그러나 정형 데이터의 피쳐들은 각각 독립적인 의미를 지니고(age, weight처럼 칼럼명을 보면 그 의미를 파악할 수 있죠) 매우 다른 분포적 특성을 가지고 있는 경우가 많습니다. 이런 피쳐들을 제일 잘 설명해주는 하나의 축을 찾아야 하고 그 축을 돌려버리는 건 의미가 없습니다. 데이터가 RI 하지 않다면, 모델도 그렇지 않아야 하는 게 아닐까요?

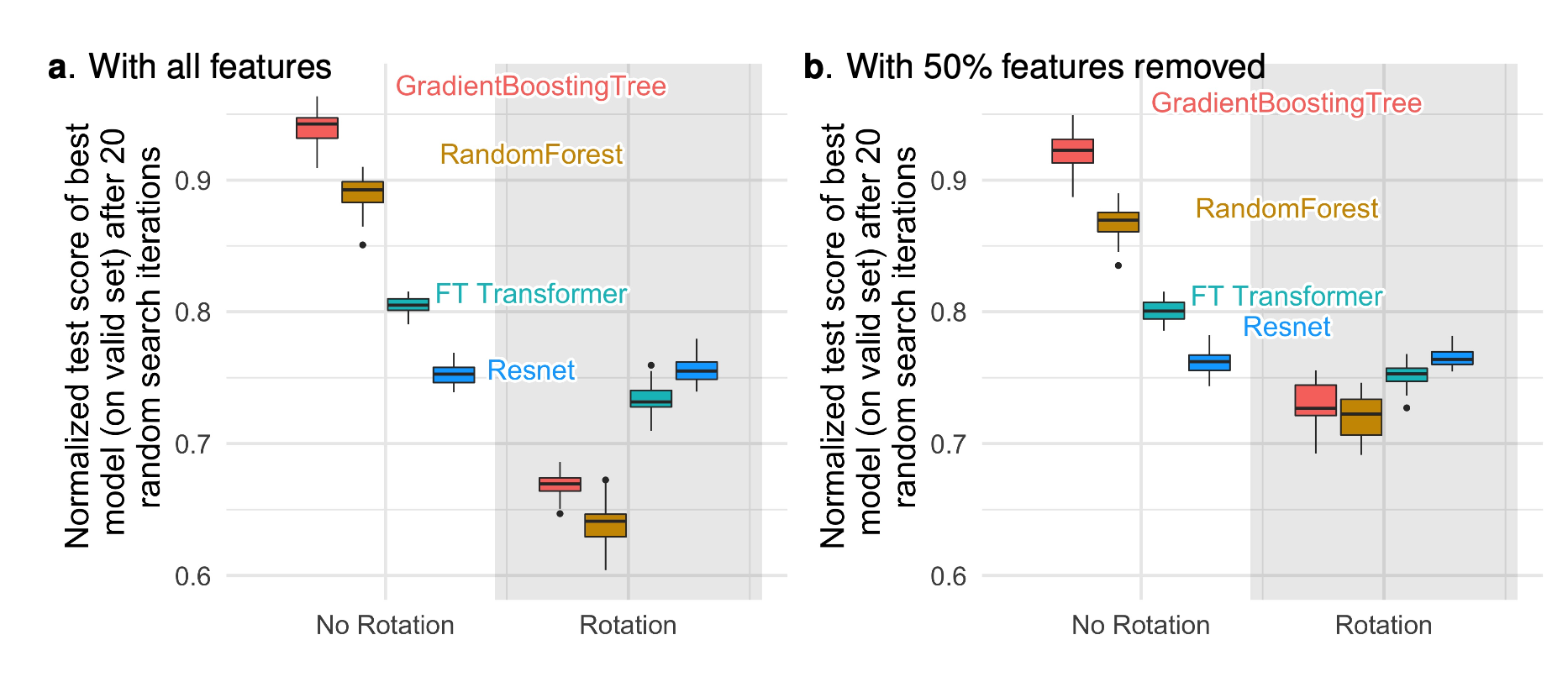
좌측 그림은 데이터에 random rotation을 적용했을 때 모델들의 성능 변화를 보여줍니다. Resnet가 완전히 똑같은 성능을 보여줌으로써 RI 모델이라는 걸 볼 수 있죠. 반면 트리 모델들은 성능이 매우 떨어진 걸 관찰할 수 있습니다. 우측 그림은 쓸모없는 피쳐 50%를 제거한 다음에 random rotation을 적용한 것인데 이 경우 트리 모델의 성능 감소가 좌측 그림에 비해 좀 덜하네요. 정형 데이터에서 서로 독립적인 피쳐들을 회전해서 섞어버리는 것은 성능에 좋지 않고, 그 중에 쓸모없는 피쳐가 많이 섞여 있으면 더 좋지 않은 거죠.

이 결과는 사실 2번의 uninformative한 피쳐들에 관한 실험 결과와도 상당히 관련이 있습니다. 앤드류 응의 이 2004년 논문은 쓸모없는 피쳐들이 매우 많아질 때 여러 지도학습 알고리즘의 RI 특성에 따라서 sample complexity(좋은 학습 결과를 내기 위한 학습 데이터의 크기)가 어떻게 다르게 증가하는지를 다루고 있는데요. 여기서 증명된 바에 따르면 RI 알고리즘의 경우 쓸모없는(irrelevant) 피쳐의 개수가 증가함에 따라 sample complexity가 선형적으로 증가한다고 합니다. 여기서 언급된 RI 알고리즘에는 L2 regularization을 적용한 로지스틱 회귀, SVM, 신경망 모델이 있습니다. 반면 L1 regularization을 적용한 로지스틱 회귀, 나이브 베이즈 분류기, 결정 트리 같은 not RI 알고리즘은 쓸모없는 피쳐가 많아져도 sample complexity가 로그 스케일로만 증가하고요.

이게 무슨 소리냐면, 극단적으로 99개의 피쳐가 타겟 변수랑 아무짝에도 상관이 없고, 딱 1개의 피쳐 $x_1$ 만 유효해서 그냥 $x_1 \ge k$ 로 임계값을 그어 뛰어난 정확도를 달성할 수 있는 매우 쉬운 문제가 주어졌을 때도, RI 알고리즘은 하나의 규칙을 배우기 위해 상당히 많은 데이터를 학습해야만 한다는 겁니다. 하지만 결정 트리가 동작하는 방식을 생각해보면 결정 트리는 단 하나의 분할(가지치기)로 그 규칙을 찾겠죠.