Post

시계열 이상 탐지할 때 데이터 분포가 바뀐다면

Posted
By pizzathiefz 17 min read

When Model Meets New Normals: Test-Time Adaptation for Unsupervised Time-Series Anomaly Detection (2024) 를 읽어보았습니다.


시계열 데이터에서 이상을 탐지하려면 보통 과거 데이터로 이후 데이터를 예측하였을 때 예측 범위에서 많이 벗어나는 경우, 혹은 학습된 정상 범위에서 많이 벗어나는 경우를 탐지하는 방법을 많이 씁니다. 후자는 사실 시계열에만 해당하는 방식은 아니긴 한데, 보통 오토인코더 같은 걸 학습시켜서 새로운 인풋에 대해 모델이 복원을 잘 못하면 이 인풋은 이상한 놈이구나(모델이 학습한 정상 데이터와 상당히 다르게 생겼구나) 하는 거죠. 어쨌든 이러한 접근들은 기본적으로 기존(과거) 데이터를 배운 모델이 정상이 무엇인지를 알고 있다고 가정합니다.


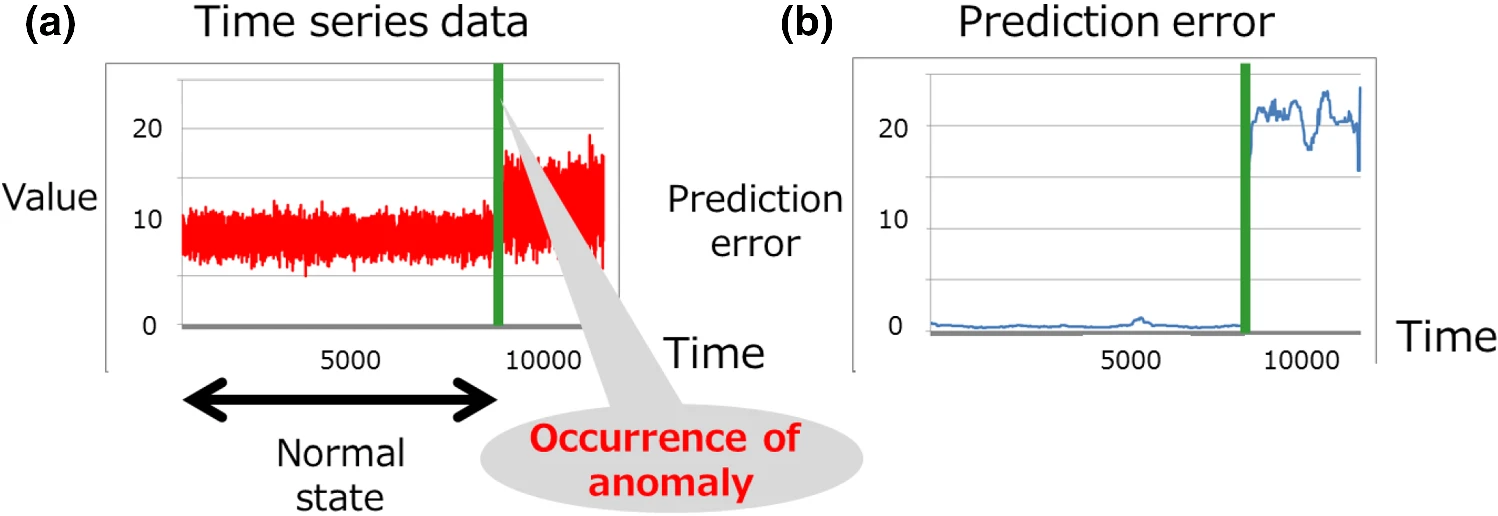이상치가 발생했을 때 과거 데이터로 학습된 모델의 예측 오차가 커진다! (출처)

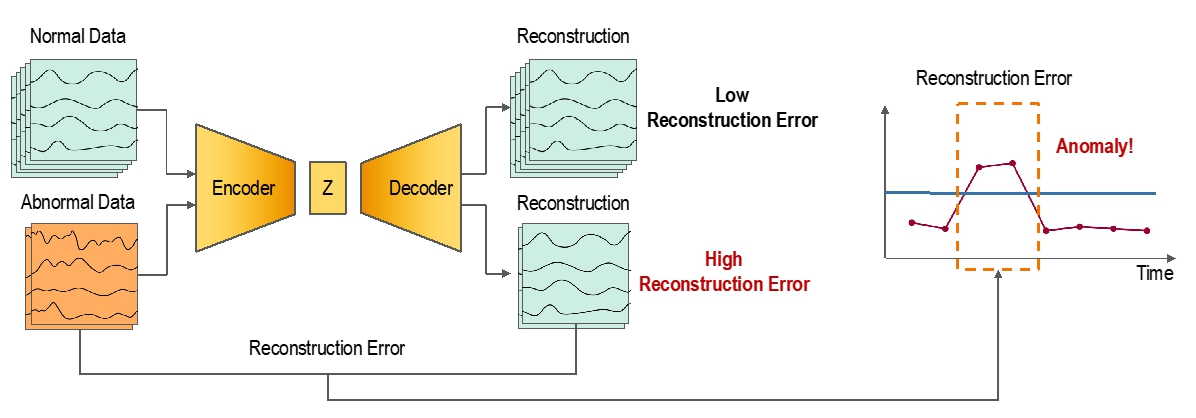이상치가 발생했을 때 정상 데이터로 학습된 모델의 복원 오차가 커진다! (출처)

문제는 무엇이 정상인지가 시간이 지남에 따라 변할 수 있다는 점입니다. 이런 걸 일반적으로 데이터의 분포 변화(shift)라고 하는데, 특히 시계열 데이터에서 테스트 데이터셋에 시간에 따른 분포 변화가 발생한 경우, 급격한 성능 저하의 원인이 될 수 있습니다.

오늘 읽게 된 논문에서는 이러한 현상을 ‘세상은 변하는데 모델만 과거에 머무르고 있는’ 상황으로 표현하는데요. 이런 데이터 분포 변화에 대응하기 위한 다음과 같은 2가지 아이디어를 제시하고 시계열 이상탐지라는 과제에서 2가지 모듈을 조합했을 때 성능과 강건함을 모두 개선한다는 결과를 보여주고 있습니다.

  1. 트렌드 추정 및 제거 (Detrend)
  2. 자기지도학습을 통해 테스트 데이터에서의 변화된 정상 패턴 (New Normal) 학습 (Test-Time Adaptation)

한장요약 사진

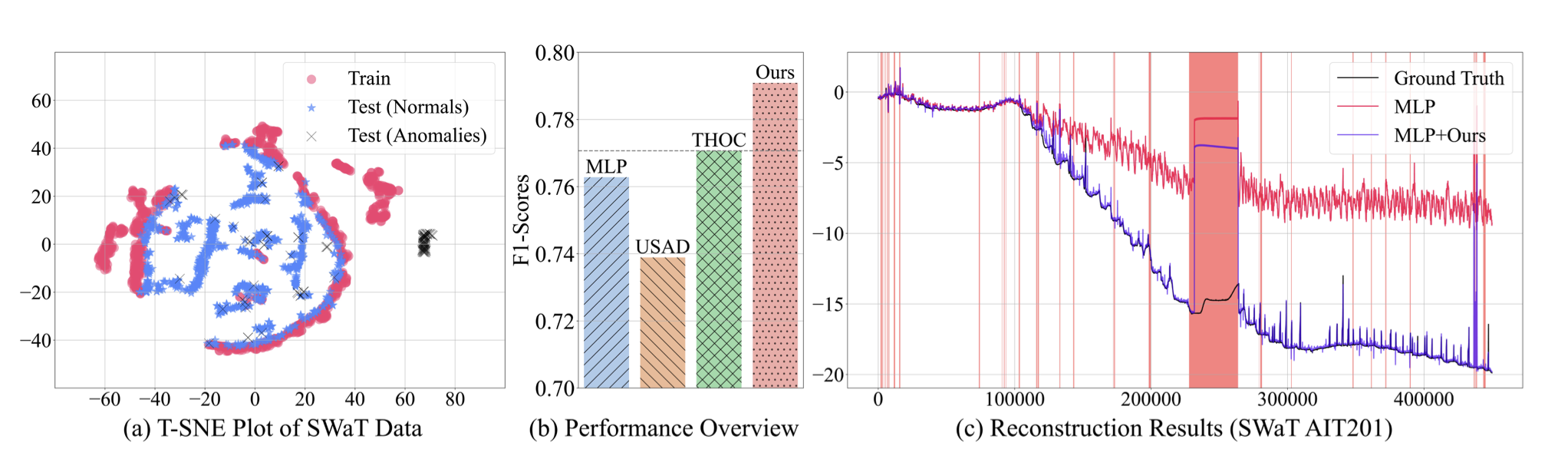
  • (a) SWaT라는 시계열 이상탐지 분야의 벤치마크 데이터셋에 대해 T-SNE 시각화. 학습 데이터와 테스트 데이터 간의 shift가 상당히 발생하는 데이터셋임을 알 수 있음.
  • (b) 간단한 MLP 기반 오토인코더를 사용했을 때도 이 논문이 제시하는 모듈을 붙인다면 F1 기준으로 기존 SOTA를 능가하더라 라는 그림.
  • (c) 복원 오차가 감소하는 걸 보면 이 논문이 제시하는 방안이 단순 MLP 모델에 매우 큰 성능향상을 불러오는 것을 확인할 수 있더라 라는 그림.

어떤 연구들은 뭔가 대단한 건 알겠지만 내 상황에 바로 적용하긴 쉽지 않아 보인다(어렵거나 너무 복잡해서 개입 가능한 요소가 많거나)..하는 생각이 드는 경우가 많은데요. 개인적으로 이 논문에서 제시하는 두 가지 모듈은 아이디어 자체도 간단하고 일반적인 내용이라서, 시계열 이상탐지에서 shift 문제를 겪고 있다면 한번쯤 써볼 만한 방법이라는 생각이 들어서 공유하게 되었습니다. 그럼 간단한 소개를 마쳤으니 자세한 내용으로 넘어가보겠습니다.


문제 정의

비지도학습 기반의 시계열 이상탐지의 목적은 주어진 라벨 없이 테스트 시간대에 비정상적인 데이터를 판별해내는 것입니다. 주어진 데이터 $\mathcal{D}$에 대해 확률 분포 $\mathbb{P}$가 있어서 예를 들어 $p(x) < \epsilon$ 과 같은 식으로 정상과 비정상을 구분할 수 있다고 할 때, 이 연구가 해결하고자 하는 것은 해당 분포가 고정되어 있지 않아서 학습 데이터의 $\mathbb{P}$와 테스트 데이터의 $\mathbb{P}$가 달라지는 현상이 발생하는 문제입니다. 기본적인 notation은,

  • $F$ 개의 Feature를 가지는 하나의 관측치 $X_i \in \mathbb{R}^F$ 에 대해 $\mathcal{D} = { X_1, X_2, \cdots, X_N }$
  • 모델(anomaly detector)는 각 관측기를 $y= \lbrace 0, 1 \rbrace$ (1이면 이상, 0이면 정상)의 예측치로 맵핑하고자 함
    • 구체적으로는 anomaly score function $\mathcal{A} (X_t) > \tau$ 이 동작해서 특정 임계값 $\tau$ 를 넘으면 이상으로 판단
    • 모델은 앞서 언급한 오토인코더 계열의 모델로, 정상 데이터만으로 이루어진 학습 데이터로 모델을 학습시킨 다음 새로운 데이터에 대해 디코더-인코더를 거쳐 복원(reconstruction) 시킨 후 원래 데이터와 복원된 데이터의 차이를 $\mathcal{A}$ 라 하자(클수록 이상함)
  • 전체 시계열 데이터가 timestamp $t$ 에서 크기 $w$ 의 sliding window로 잘린 부분 시퀀스로 전처리되는데 무슨 말이냐면
    • $\mathcal{X} = \lbrack X_{t-w+1}, X_{t-w+2}, \cdots, X_{t-1}, X_t \rbrack$
    • $\mathcal{Y} = \lbrack y_{t-w+1}, y_{t-w+2}, \cdots, y_{t-1}, y_t \rbrack$


제안하는 방법

Detrend

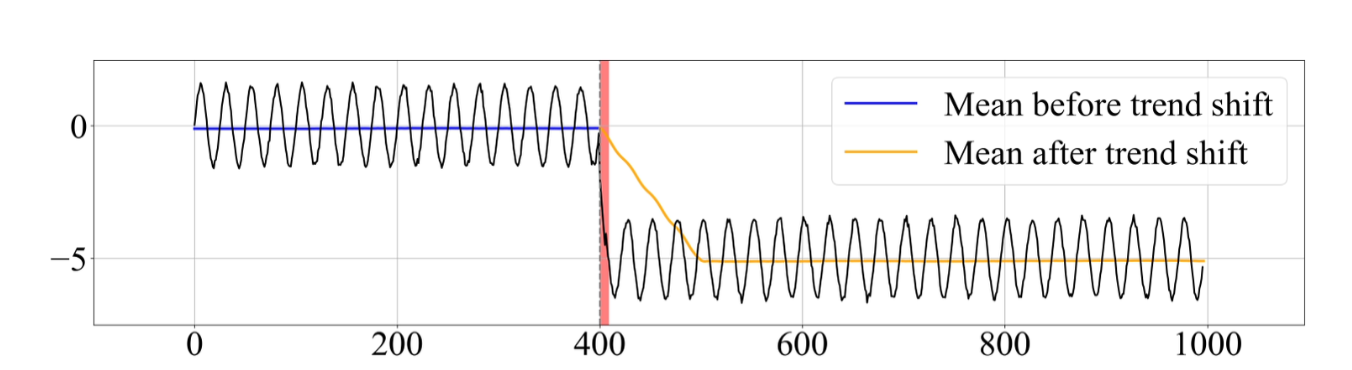
첫번째 방안은 추세 제거(Detrend)입니다.

위와 같은 경우를 추세(Trend)의 변동이 발생했다고 합니다. shift 발생 전후를 대조해봤을 때 패턴이 바뀌지는 않았지만 평균적인 값이 내려간 것이죠. Detrend 모듈의 아이디어는 이동평균(EMA; Exponential Moving Average)를 통해 이 추세의 변동량을 추정해서 그걸 그냥 없애주면 되지 않겠냐는 것입니다.

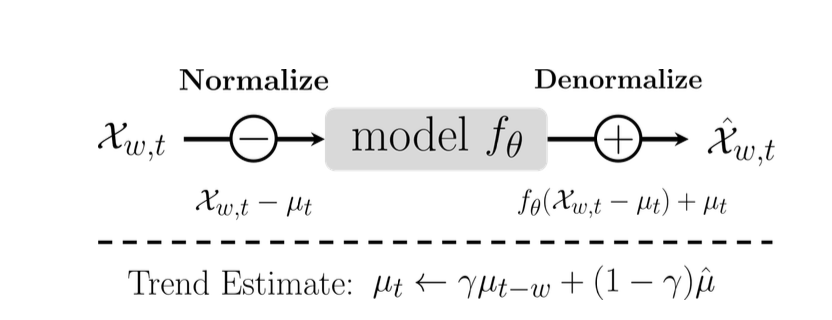
우선 추세 추정치(Trend Estimate)을 뜯어보면요, 다음과 같이 계속 이전 timestamp 기준 시퀀스에 새로 들어오는 시퀀스의 평균을 버무려서 이동평균 통계량을 만든다고 볼 수 있습니다.

  • $\hat{\mu} = \frac{1}{w} \sum^t_{i=t-w+1}X_i$ 즉 현재 stream data(아까 언급한 sliding window로 자른 시퀀스)의 평균
  • $\mu_{t-w}$ 는 이전 시퀀스의 추세 추정치
  • $\gamma$ 는 EMA 값을 구할 때 이전 시퀀스 평균과 이전 시퀀스 평균 비중을 조정하는 하이퍼파라미터

그러면 저 위의 도식도가 나타내는 것은 매 시퀀스가 들어올 때마다 추세 추정치를 빼서 모델에 넣고, 모델의 아웃풋에 다시 추세 추정치를 더해준다 라는 아주 간단한 작업이 되겠습니다. 쉽게 말하면 모델한테 추세로 인해 발생하는 변동은 빼고 생각해! 라고 말해주겠다는 것입니다.

TTA(Test-Time Adaptation)

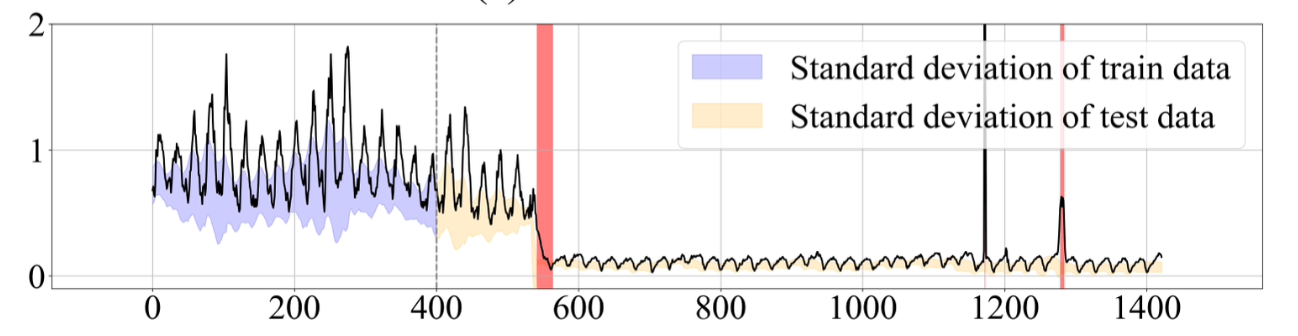
그러나 다음 그림처럼 추세 변동만으로 설명되지 않는 유형의 shift가 존재합니다. 이에 대한 해결 방안으로 두번째로 제시되는 것이 바로 TTA(Test-Time Adaptation)입니다.

사실 TTA는 이 연구에서 처음 만들어낸 것은 아니고, 주로 CV 분야에서 역시 학습-테스트 데이터 분포 변화에 대응하기 위해 연구되어 온 주제로, 추가적인 라벨이나 학습 데이터 없이 새로운 분포에 일반화할 수 있는 방향으로 모델 파라미터를 업데이트 하는 테크닉입니다. 테스트 데이터에서 entropy를 최소화 하도록 파라미터를 업데이트한다거나, 학습된 모델의 예측을 일종의 pseudo-label로 사용하는 등 여러 가지 방법이 제시된 바 있습니다.

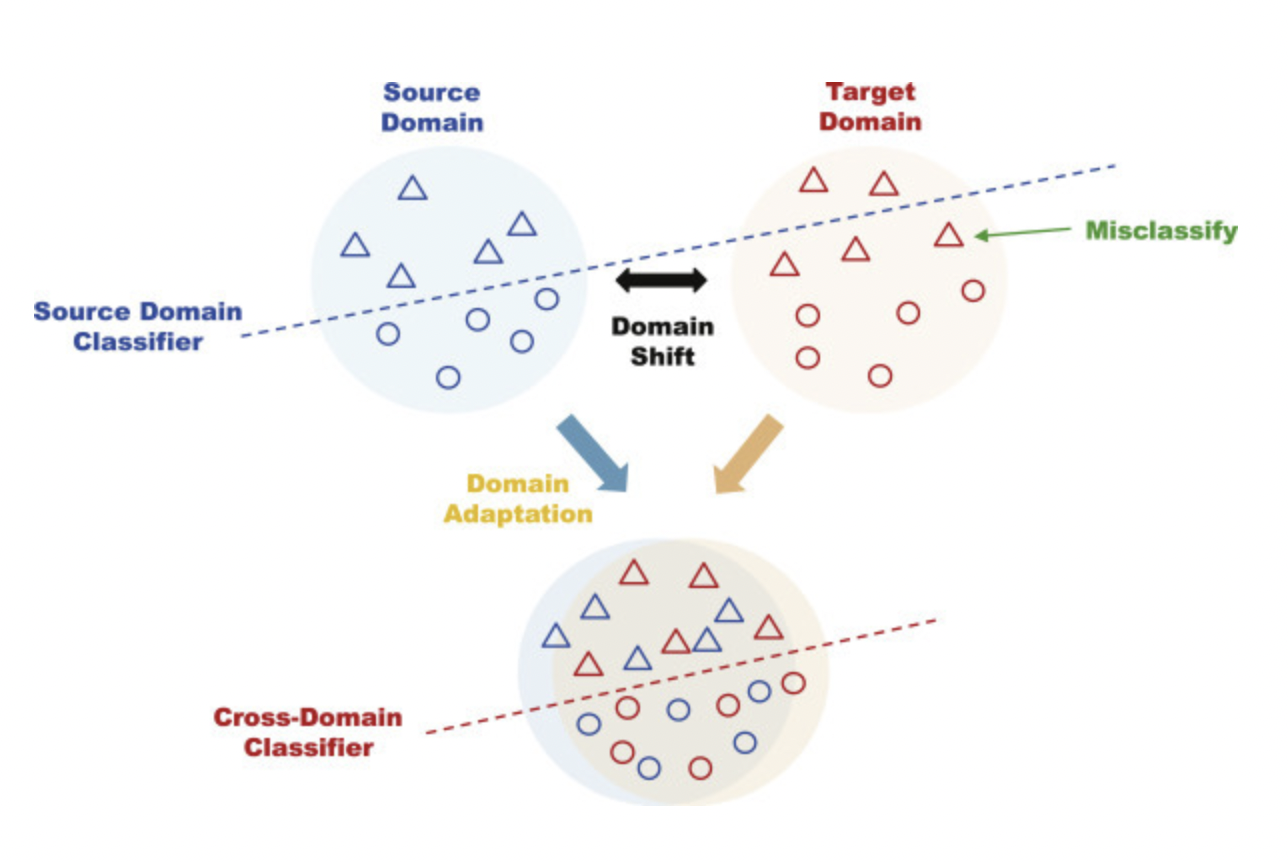TTA를 개념적으로 이해할 수 있는 그림 (출처)

이 연구가 제시한 TTA 방식에서 가장 중요한 점은 시계열 이상탐지 태스크에 맞게 비지도학습으로(ground truth를 전혀 사용하지 않고) 모델을 업데이트하되, stream 데이터 중에서도 모델이 이미 알고 있는 정보 기준으로 이상으로 판단되는 데이터는 사용하지 않는다는 것입니다.

조금 더 자세히 설명하면,

  • 모델이 학습되었을 때 Anomaly Score의 분포(percentile) 기준으로 복원 오차에 대한 임계값 $\tau$를 정한다. (이걸 정하는 건 하이퍼파라미터임)
  • stream되는 테스트 데이터에 대해서 해당 임계값을 기준으로 Pseudo-label을 만든다.
    • 즉 학습된 모델이 생각할 때 이상인 데이터와 정상인 데이터를 나눈다.
  • 정상인 데이터에 대해서만 손실을 역전파한다.


실험 결과

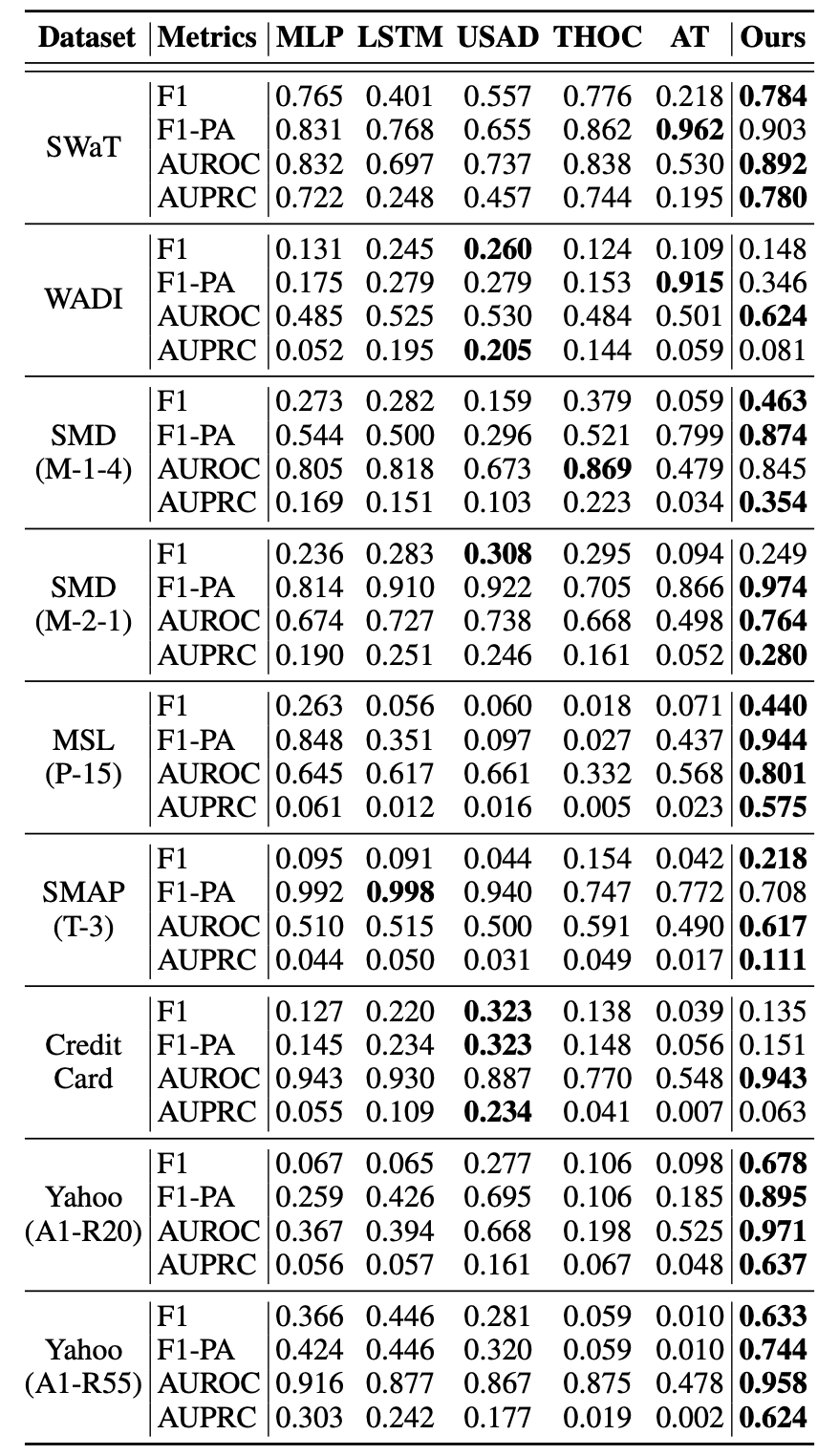
9종에 벤치마크 데이터셋에 대해 여러 모델들 - 기본 MLP Autoencoder, LSTMEncDec, USAD, THOC, AT(Anomaly Transformer) - 과 본 논문의 제안 방식인 MLP Autoencdoer+Detrend+AAT (테이블 내 Ours로 표기) 의 성능 비교를 실험한 결과입니다.

평가 메트릭은,

  • F1, F1-PA (F1-Point Adjustment)
    • F1-PA는 뭔가 했더니 특정 세그먼트 내에 이상을 하나라도 탐지했으면 (그 다음에 현업에서 세그먼트를 검사한다고 가정하고) 그 세그먼트 전체를 맞힌 걸로 쳐주는 상당히 긍정적인 메트릭..
  • AUROC, AUPRC
    • 임계값과 무관하게 detector의 전반적인 성능을 볼 수 있도록 함
    • 이상탐지는 대부분 매우 불균형한 클래스가 특징이므로 AUPRC 포함

  • 표가 너무 기니까 중요한 점만…
    • 이 연구의 문제의식은 Train-Test Shift가 발생한 상황에서의 해결이기 때문에, 각 벤치마크 데이터셋별로 학습 데이터와 테스트 데이터의 분포 차이를 KL Distance로 계산한 결과를 같이 보고하여 봤을 때
      • 위 데이터셋 중 거의 shift가 발생하지 않은 데이터셋이 있는데(Credit Card) 성능을 보면 모든 지표에서 거의 성능이 떨어지는 것을 확인할 수 있음
      • 반면 SwaT처럼 shift가 가장 큰 데이터셋에서는 AUROC,AUPRC에서 상당한 성능 개선 확인
    • 재미있는 점은 SOTA 모델 중 하나인 Anomaly Transformer가 일부 데이터에서 본 논문의 모델보다 F1-PA만 잘 나온다는 것인데 (나머지 F1, AUROC, AUPRC는 처참하게 낮음) AT는 문제가 있는 특정 구간을 잡아내지만 pointwise로 정확한 판단은 못하고 있다는 걸 알 수 있음

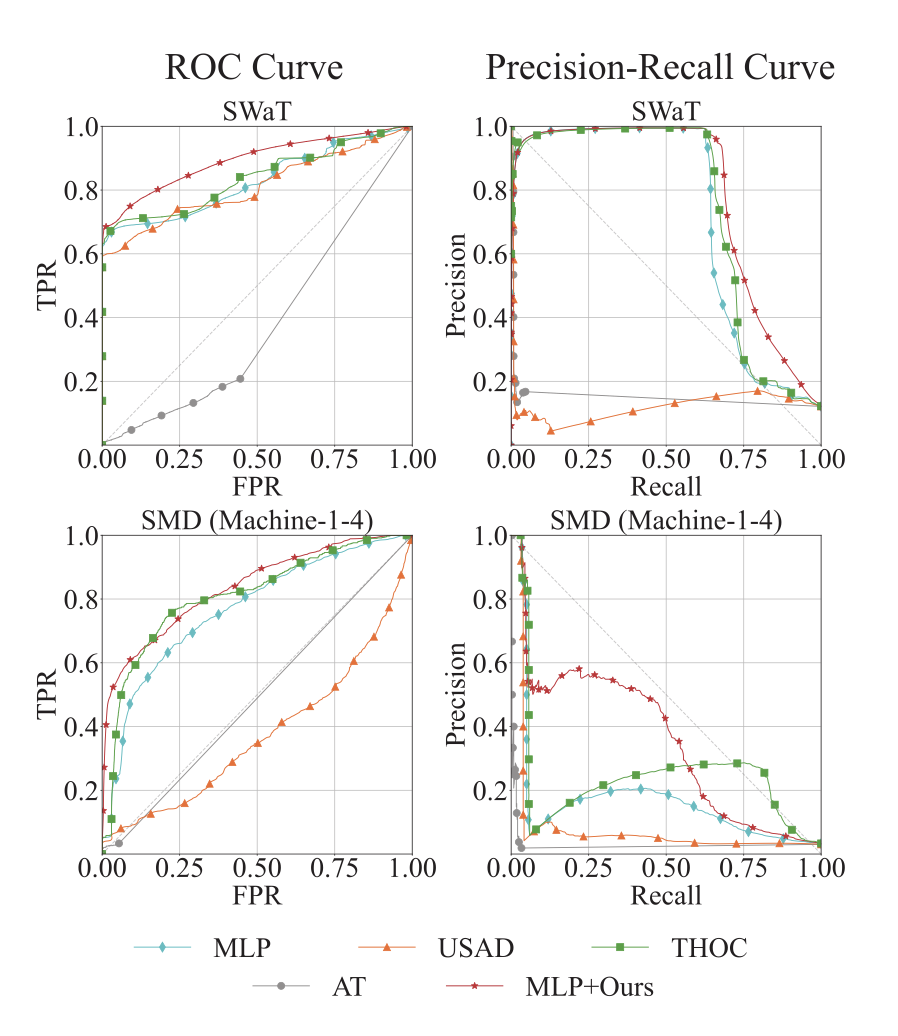
다음은 ROC Curve와 Precision-Recall Curve입니다. 제안된 두 개의 모듈이 있는 버전의 모델(빨간색)이 없는 버전의 모델(하늘색)의 성능을 유의미하게 개선하는 것을 확인할 수 있습니다. 또한 전반적으로 성능이 임계값에 매우 크게 영향을 받을 거라는 점도 눈에 들어오는데요. 일반적으로 분류모델 적합 후에 Curve를 그려서 Best F1을 만드는 임계값을 찾는 방식을 많이 하는데, 사실 스트림 데이터가 들어오는 현실세계 상황에서는 적합한 임계값을 정하는 게 어려울 수 있다는 점도 언급을 하고 있습니다.

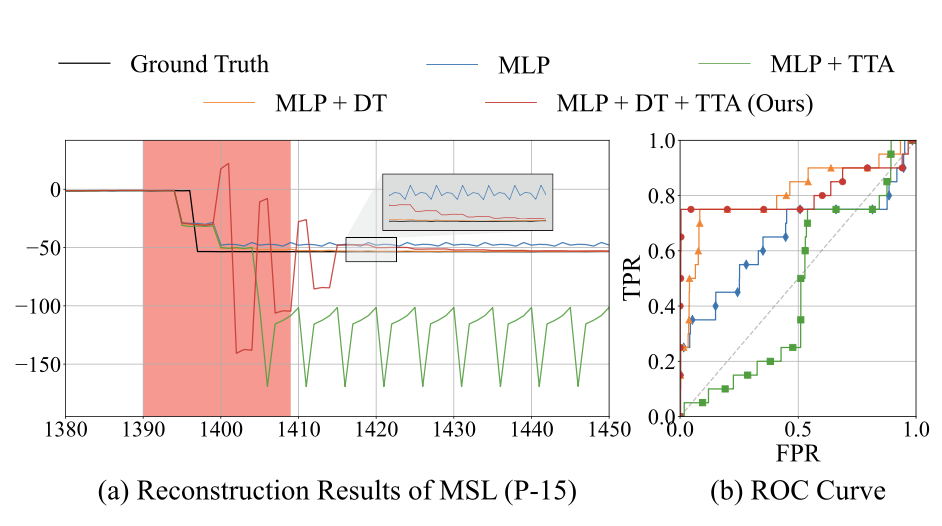
마지막으로 추가한 모듈을 제거해보는 실험입니다.

  • 확대된 부분을 잘 보면, MLP+DT+TTA와 그냥 MLP의 비교 - 그냥 MLP(파란색)은 trend shift가 일어난 후에도 복원 오차가 계속적으로 발생함
  • TTA 없이 DT만 사용한 경우 sensitivity가 떨어져서 새로운 데이터로 모델을 업데이트하는 게 sensitivity에 기여한다는 것을 알 수 있음
  • DT 없이 TTA만 사용한 경우는 trend shift가 일어나기 전 데이터 시퀀스에 오버피팅되어 모델의 강건함이 많이 떨어짐
  • 즉 결론적으로는 제안된 방식 둘을 같이 사용했을 때 가장 결과가 좋았다! 라는 결론
Posts, Data
time-series anomaly-detection
This post is licensed under CC BY 4.0 by the author.