단변량 분포 간 거리 함수

콜모고로프-스미르노프 검정와 바서슈타인 거리를 포함하여 단변량 분포 간의 거리 함수를 다룹니다. Detecting Anomalies Using Statistical Distances / SciPy 2018 를 바탕으로 정리한 내용입니다.

주어진 베이스라인 분포가 있을 때 이를 새로운 데이터의 분포와 비교해서 둘이 다른지 확인하고 싶다고 합시다.

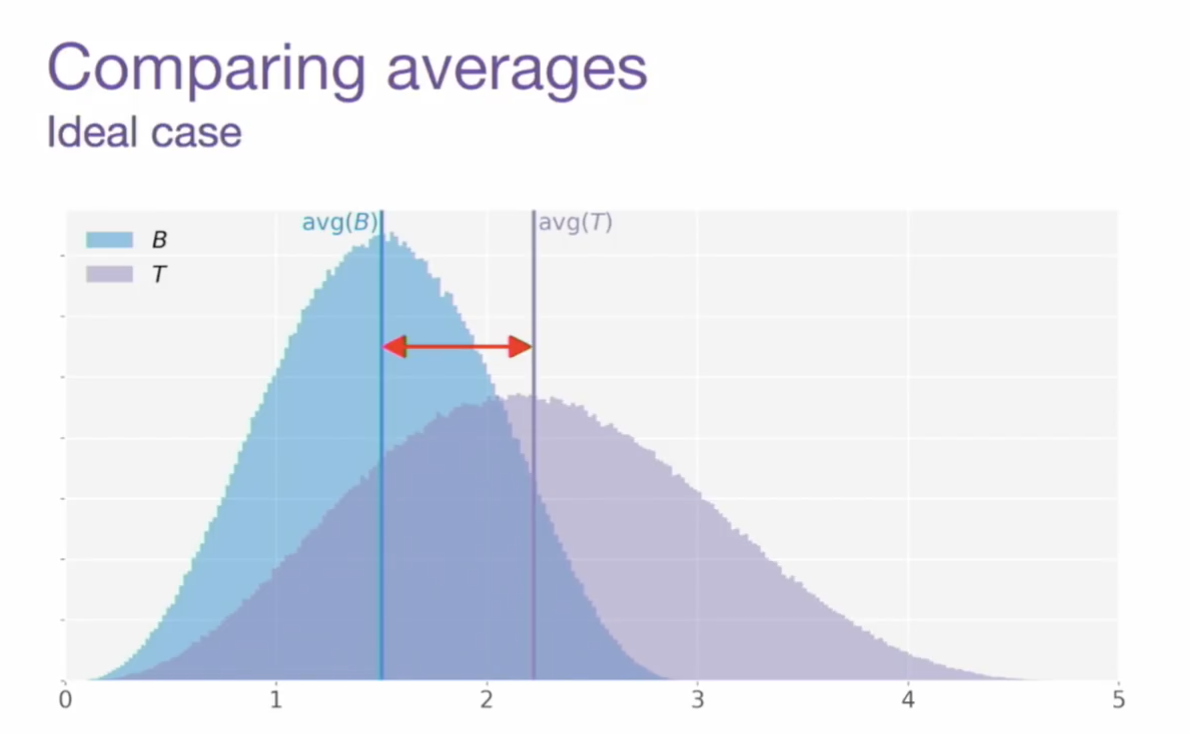
가장 간단한 방법은 평균과 같은 표본통계량을 사용하는 것입니다.

• (1) 평균을 비교했을 때 분포의 차이를 확인할 수 있는 케이스
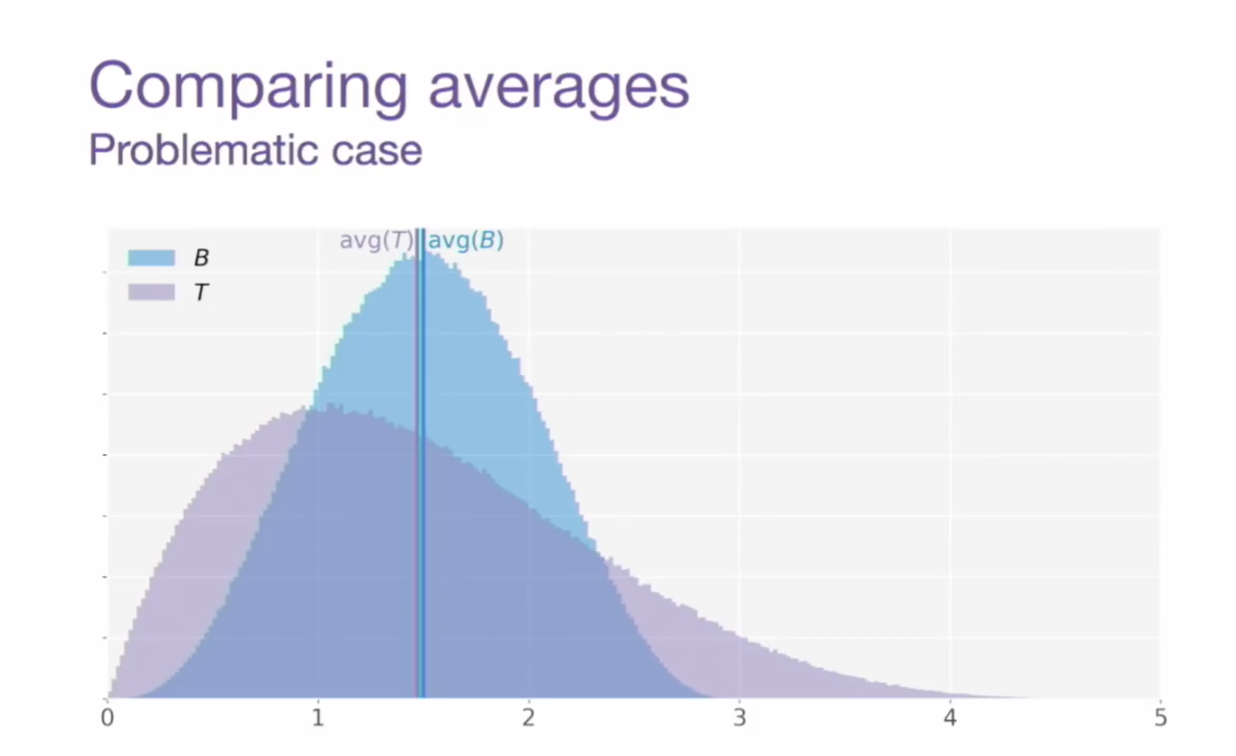
• (2) 평균은 같은데 … 둘을 같은 분포라고 볼 수 있는가? 🤔

평균 말고 quantile 등을 이용할 수도 있지만, 마찬가지의 문제가 나타날 수 있죠. 이때 가능한 해결책은 두 가지입니다.

1. 통계량을 여러 개 합쳐서 사용한다. → 표본도 같고 분산도 같고 95% quantile도 같고 등등 다 같으니 두 분포는 같네! 라고 결론 내리기.
2. 통계적 거리(statistical distance) 를 사용한다.

오늘은 2번째 방법인 분포 간의 통계적 거리에 대해서 간단히 정리해 보았습니다. 아래 등장하는 거리 함수들은 SciPy의 stats을 통해 파이썬으로 매우 쉽게 써먹어볼 수 있습니다!

Kolmogorov-Smirnov Test

콜모고로프-스미르노프 검정은 정해진 특정 분포로부터 샘플 분포가 나온 것인지를 테스트하거나, 두 샘플이 같은 분포에서 나왔는지 테스트할 때 씁니다. 그래서 보통은 정규성 검정에 많이 쓰고 기초통계학 시간에 샤피로-윌크스 등이랑 짝으로 나오는데, 저도 사실 최근까지 정규성 검정에만 쓰는 줄 알았습니다. 특정 분포에 대한 가정 없이 2표본 간 비교가 가능하다는 것이 중요한 점입니다.

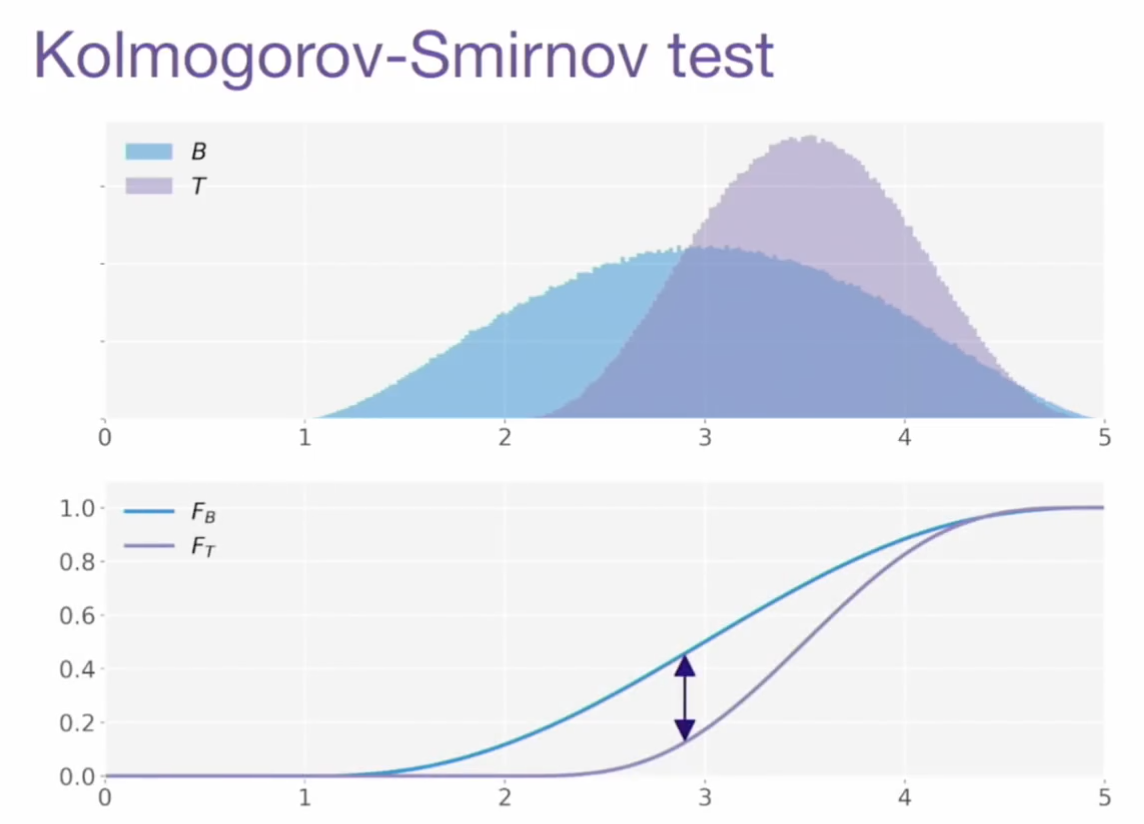
• 기본 개념: 두 분포의 누적분포함수(CDF)의 거리의 최대값 (maximum absolute difference)를 통계량으로 얻는 것이다. (→ 따라서 당연히 0과 1 사이이게 됨)

\[KS(T,B) = \sup_{x \in \mathbb{R}} \vert F_T(x)-F_B(x)\vert\]

• 영가설은 두 샘플이 같은 분포에서 나왔다는 것이고 특정 유의수준(예 - 0.05)에서 p값이 그보다 작으면 가설을 기각한다(같은 분포라고 볼 수 없다고 본다).
• 사실 영가설을 기각하느냐 마느냐인 테스트이기도 하지만, KS 값 자체를 거리(두 분포가 얼마나 떨어져 있는지 metric)으로 사용될 수 있다.
  • $KS(X,Y) \ge 0$ (non-negativity)
  • $KS(X,Y) =0 \iff X=Y$ (identity of indiscernibles)
  • $KS(X, Y) = KS (Y,X)$ (symmetry)
  • $KS(X, Z) \le KS(X,Y) + KS(Y,Z)$ (triangle inequality)

거리 함수가 되려면, 모든 분포 $X$, $Y$, $Z$에 대해 요런 성질들을 만족해야 한다고 하네요. 거리 함수이기 때문에 탐지 알고리즘이나 클러스터링 등을 적용할 수 있다는 점에서 유용합니다.

K-S 거리의 문제점

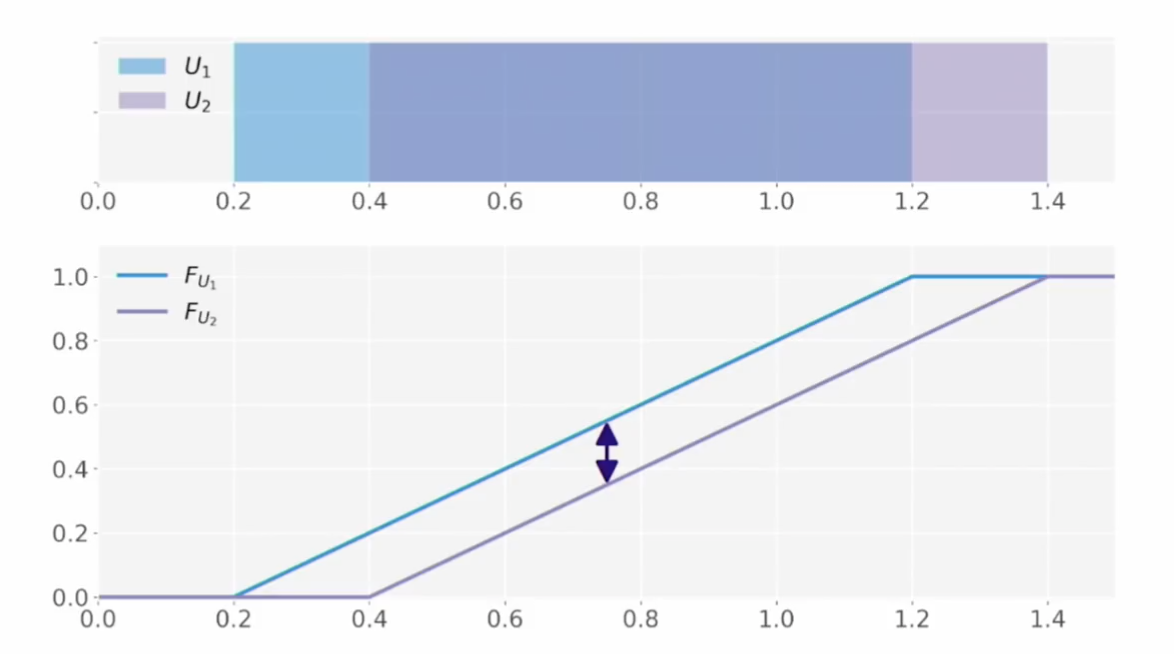
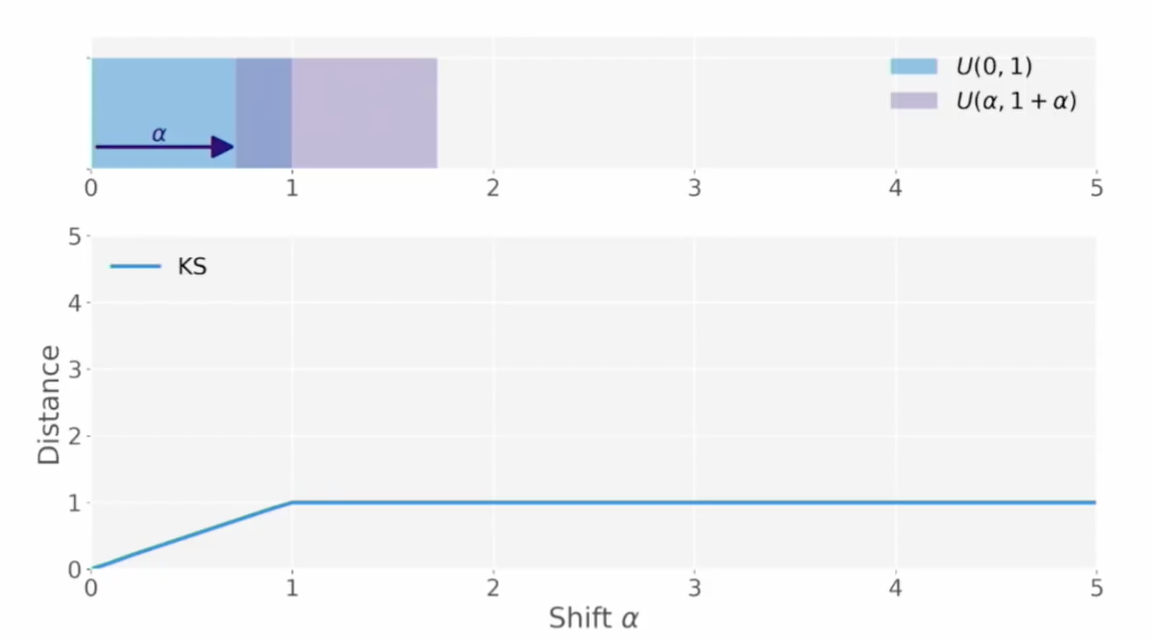
• 두 개의 균등 분포(uniform distribution)이 있을 때 이 두 분포의 KS 값은 첫번째 그림처럼 계산될 것이다.
• 만약 둘 중 하나를 골라서 $\alpha$ 만큼 옆으로 밀어버린다면?
  • 조금 밀면 KS 거리는 증가하지만, 일정 이상의 멀어진 거리는 값에 반영이 안 된다.

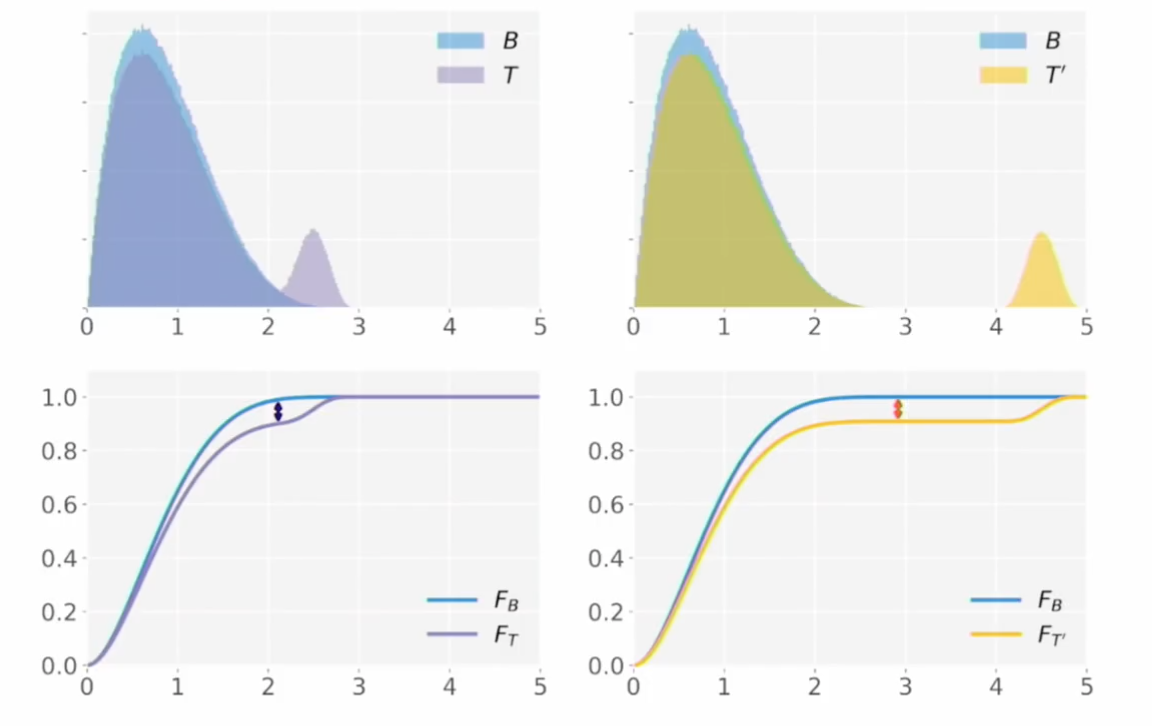
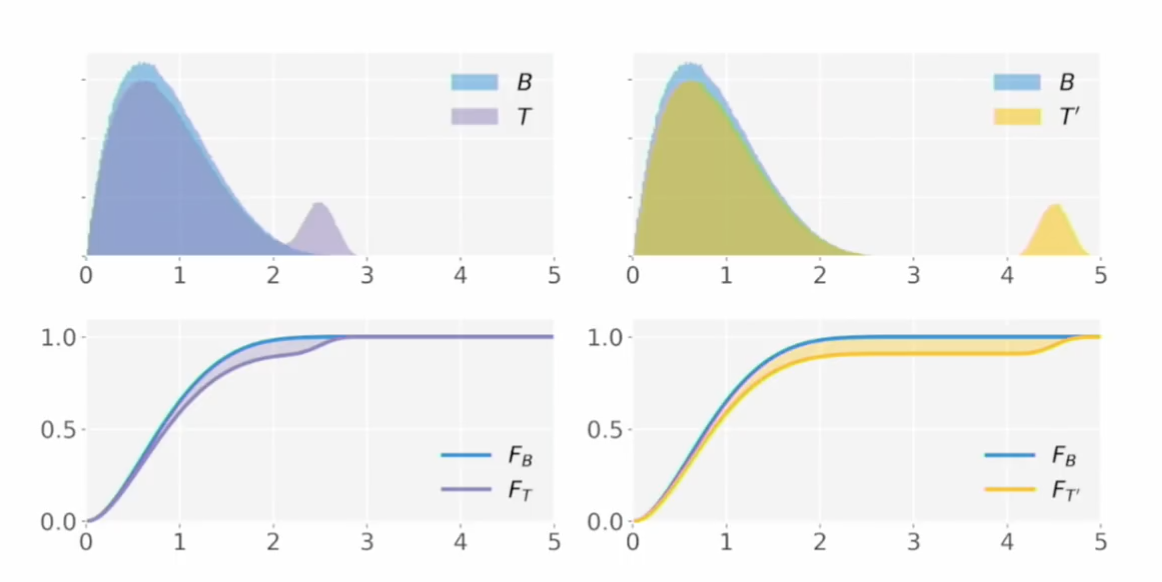
이처럼 두 분포가 겹치지 않을 정도로 떨어진 정도가 커질수록(옆으로 더 멀리 밀어버릴수록) 분포가 더 심하게 달라져야 하는 게 맞는데, KS 거리는 커지는 것이 한계가 있는 현상입니다. 이런 현상은 다음과 같은 분포에서 문제가 됩니다.

$T’$는 양봉의 오른쪽 부분이 $T$보다 멀리 떨어져 있으므로, $T’$가 baseline 분포인 $B$와 떨어진 정도는 $T$가 $B$와 떨어진 정도보다 커야 하지만 KS 거리로는 둘이 큰 차이가 없다는 것입니다.

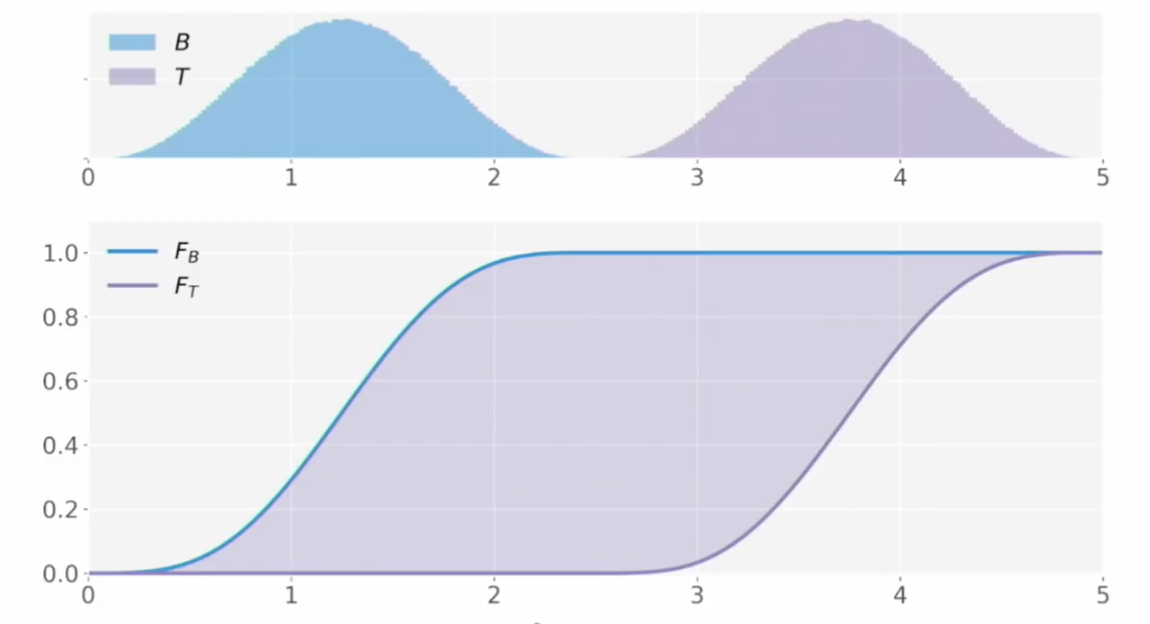
Earth Mover’s Distance

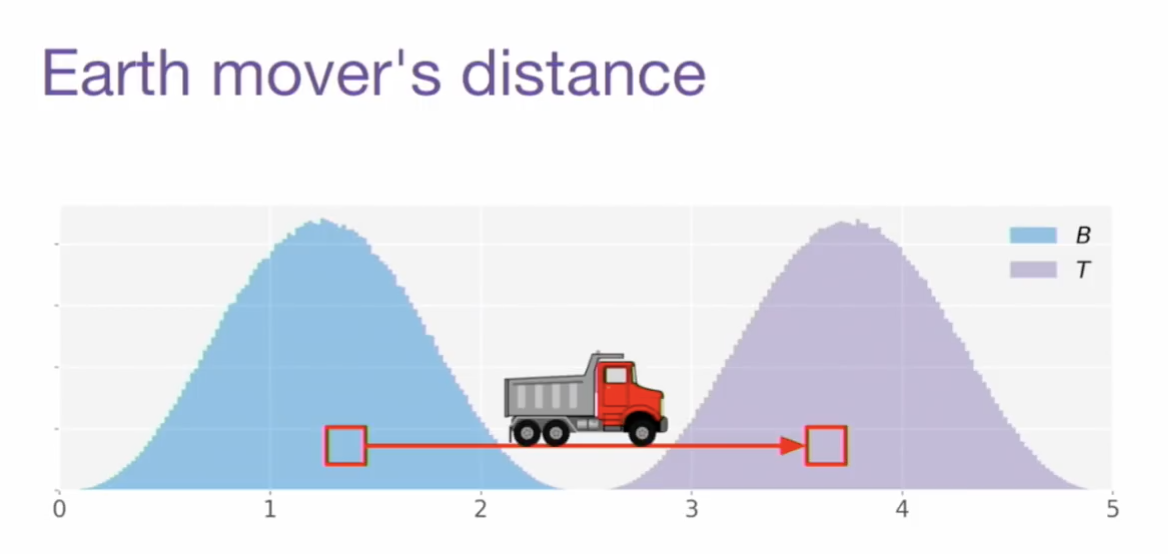
두번째 거리 함수는 GAN이랑도 종종 같이 등장하는(W-GAN), Earth Mover라는 괴상한 이름을 가진 친구입니다. 혹은 바서슈타인 거리(Wasserstein Distance) 라고도 합니다. 하나의 분포를 산이라고 생각할 때, 이 산을 다른 산으로 옮기는 데 드는 수고(일)의 양을 거리로 본다는 측면에서 이렇게 부릅니다.

• 분포를 $B$에서 $T$로 옮긴다고 하면 EMD는 아래와 같이 정의될 수 있다.
  • $\gamma$ 라는 맵핑은 옮겨야 하는 흙의 양을 정해준다. $\vert x-y \vert$ 는 얼만큼 멀리 갖다 놔야 하는지를 의미하는 이동 거리이다.
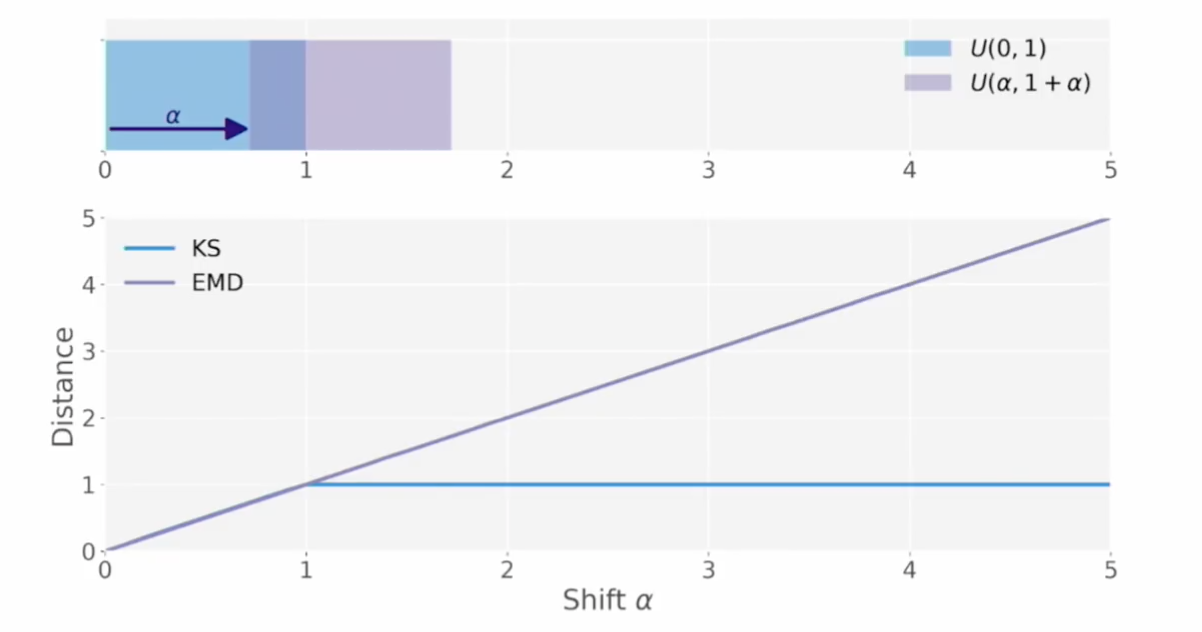
  • EMD는 흙의 양이 많아서(분포의 모양이 다르게 생겨서) 늘어나기도 하지만 절대적 거리가 멀어서 늘어나기도 한다.

\[EMD(B,T) = W_1(B,T) = \inf_{\gamma \in \Gamma(B,T)} \int_{\mathbb{R} \times \mathbb{R}} \vert x -y \vert d \gamma(x,y)\]

• EMD는 $\alpha$ 의 증가에 따라 달라지는 분포의 정도를 잘 반영하고 있다.

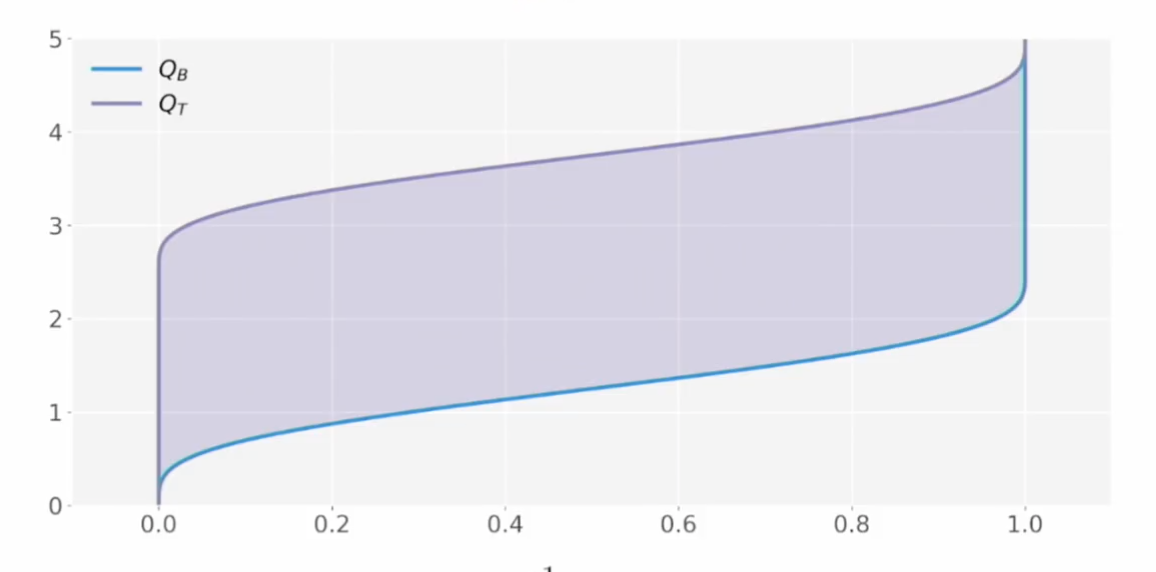
• 계산이 복잡할 것 같지만 quantile function을 통해 계산할 수 있다.

  \[EMD(B,T) = \int_{\mathbb{R}} \vert F_B(x) -F_T(x) \vert dx = \int ^1 _0 \vert Q_B(x)-Q_T(x) \vert dx\]

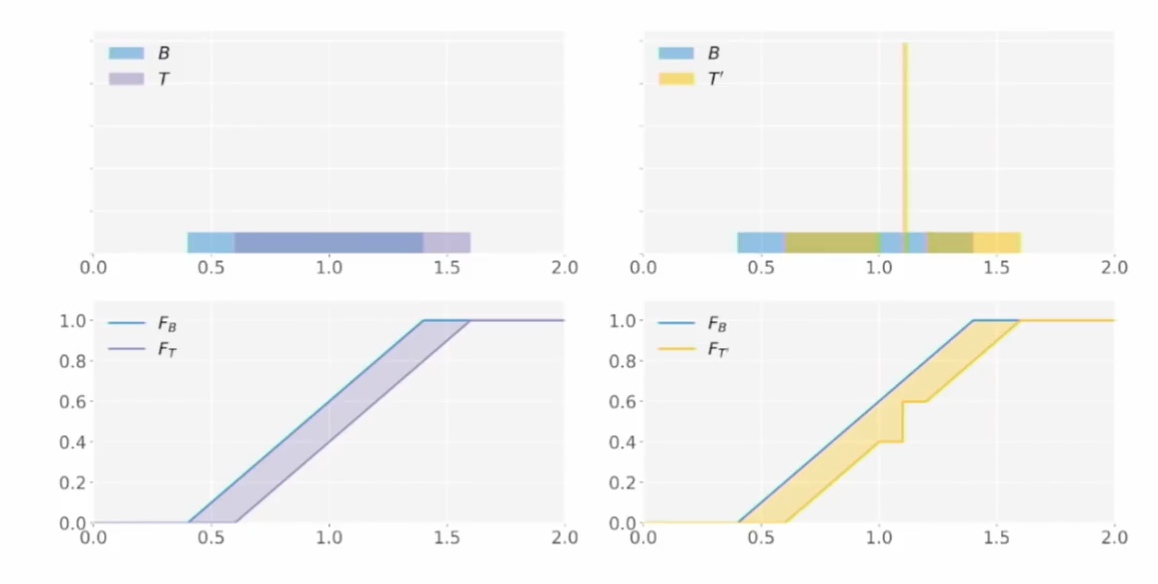
• 이제 $T’$은 $T$보다 더 먼 거리(더 먼 EMD값)으로 표현될 수 있다.

• 다만 특정 값이 지나치게 몰려있는 (local deformation) 구간이 발생한 이런 $T’$은 EMD로 잘 표현이 안 된다.
  • 이 경우, 차이가 매우 클 때 더 민감하게 penalty를 주도록 하면 되는데 다음과 같이 p-th Wasserstein distance로 바꾸면 된다. 이것도 quantile function으로 계산하는 것은 동일하다!

\[W_p(B,T) = \left( \inf_{\gamma \in \Gamma(B,T)} \int_{\mathbb{R} \times \mathbb{R}} \vert x -y \vert ^pd \gamma(x,y) \right)^{1/p}\]

$p=2$인 경우를 따로 Cramér-von Mises distance 라고 부르기도 한답니다. 이름이 너무 많네요.

from scipy.stats import ks_2samp, wasserstein_distance, energy_distance

이 거리들은 이렇게 간단히 사용할 수 있습니다. energy_distance 는 Cramér-von Mises distance의 non-distribution-free 버전이라고 합니다. 모두 1D 분포 2개를 input으로 받게 되어 있고요, 그냥 샘플 array 2개를 넣어도 되고 값과 weight를 쌍으로 넣어도 됩니다.

값과 weight를 쌍으로 넣는다는 것의 의미는, 예를 들어 분포 $U$와 $V$의 거리를 잴 건데, 이렇게 써야 합니다.

wasserstein_distance([0, 1], [0, 1], [3, 1], [2, 2])

$U$는 0이라는 값의 weight이 3, 1이라는 값의 weight이 1인 분포이고 $V$도 같은 값을 가지지만 0과 1의 weight이 동등한 분포라는 것입니다. weight의 경우 합이 1이도록 정규화될 수 있도록 positive & finite 해야 합니다.

그리고 ks_2samp 는 사실 검정을 위한 함수이므로 K-S 거리 값(검증 대상인 통계량)과 그것의 p-value를 튜플로 돌려준다는 점을 유의합시다!

SciPy Reference Guide

• ks_2samp
• energy_distance
• wasserstein_distance