DTW로 시계열 클러스터링하기

이 글을 읽으면 DTW(Dynamic Time Warping)라는 시계열 데이터에서 유용하게 쓰이는 거리 개념을 이해할 수 있고, Python으로 DTW 기반의 시계열 클러스터링(K-means, DBSCAN, Hierarchical)을 해볼 수 있습니다.

DTW(Dynamic Time Warping) 이해하기

(그림 출처)

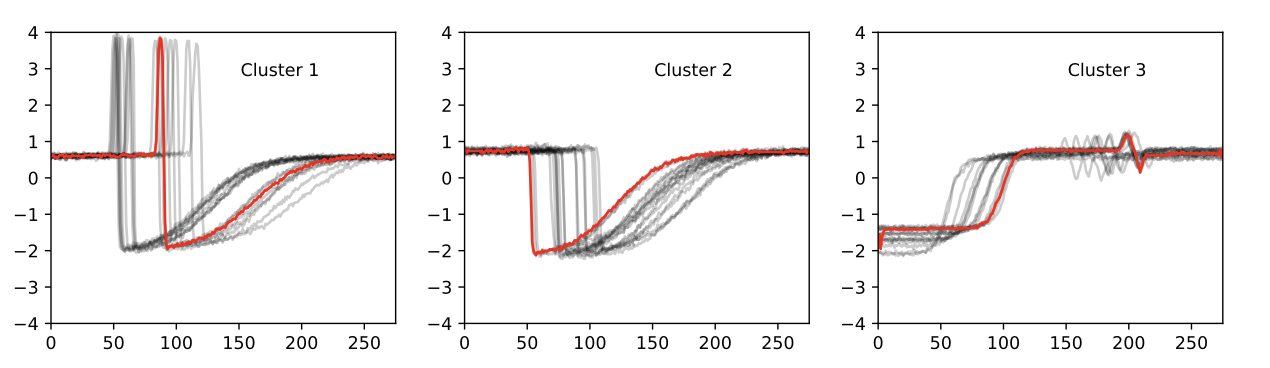
라벨이 없는 시계열 데이터를 가지고 있는 상황에서 위 그림처럼 비슷한 시계열끼리 묶어보고 싶다고 합시다. 이런 것을 보통 클러스터링(군집화)이라고 부르는데요. 클러스터링에는 많은 기법들이 있지만, 대부분 개념적으로는 다음과 같은 동일한 목표를 지닙니다.

같은 군집에 속하는 데이터끼리는 최대한 비슷하고, 다른 군집에 속하는 데이터끼리는 최대한 다르게 군집을 나눈다.

이 목표를 이루려면 알고리즘 이전에 ‘비슷하다’와 ‘다르다’에 대한 정의가 필요할 것입니다. 즉 두 개의 서로 다른 데이터 A, B가 주어졌을 때 A와 B가 얼마나 수치적으로 비슷한지에 대한 수식이 필요합니다. 비슷하다/다르다는 의미에서는 유사도라고 하고, 가깝다/멀다라는 의미에서는 거리라고도 하는데 사실 같은 소리입니다.

대표적으로 많이 쓰는 방식으로는 유클리디언 거리(ED; Euclidean Distance)가 있죠.

\[ED(p,q) = \sqrt{(p_1-q_1)^2 + \cdots +(p_n-q_n)^2 }\]

이런 식이 하나 있다면 우리는 A=(34,10), B=(23,4), C=(46,2) 이런 데이터들이 있을 때 A와 B의 거리는 12.5과 A와 C의 거리는 14.4니까 C보다 B가 더 A와 비슷하네 라는 결론을 내릴 수 있는 것입니다.

시계열에 필요한 거리 개념

문제는 지금 우리가 가지고 있는 것이 시계열 데이터라는 것입니다. 가장 많이 쓰는 ED를 쓰고 싶지만, ED는 시간의 흐름에 따라 동일한 패턴으로 변화하지만 시작점이 다른 데이터의 특성을 반영하지 못합니다. 예를 들면 이렇습니다.

(그림 출처)

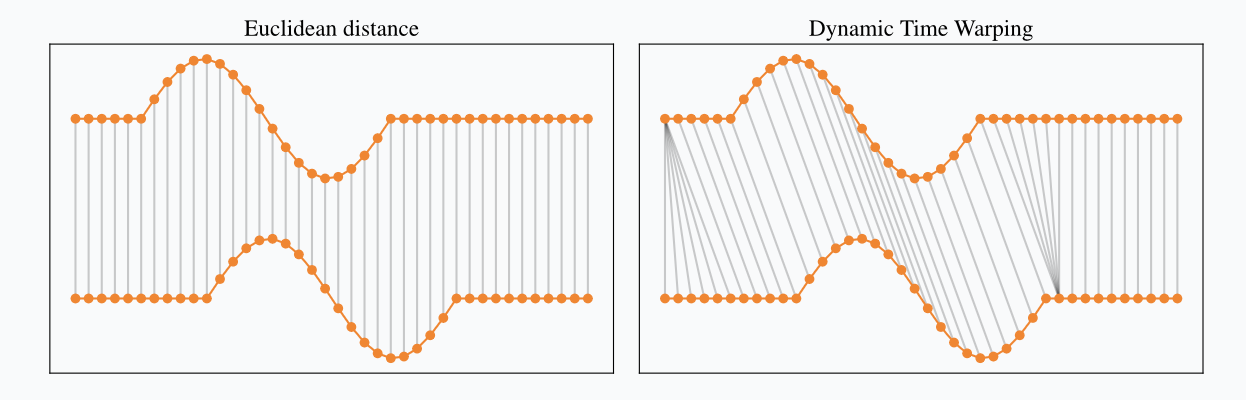
이 아래/위 시계열은 사실상 거의 동일한 패턴입니다. 다만 아래 시계열이 위의 시계열에 비해 약간의 딜레이(lag)가 발생하는 모습을 보이고 있죠. 만약 ED로 이 두 시계열의 거리를 재게 되면 왼쪽 그림처럼 이러한 시간차 패턴을 전혀 반영하지 못하고, 두 시계열이 상당히 다른 데이터라고 결론을 내리게 될 겁니다. 만약 오른쪽 그림처럼 시계열의 패턴을 고려하면서 거리를 계산할 수 있다면 어떨까요?

DTW(Dynamic Time Warping) 은 말 그대로 ‘동적으로(유연하게) 시계열을 비틀어서’ 두 데이터 간의 유사성을 판단할 수 있게 해주는 알고리즘이며,

• 시계열의 길이가 달라도
• 약간의 시간차를 두고 동일한 패턴이 발생해도 거리를 계산할 수 있다는 장점이 있습니다.

DTW 계산하는 법

어떻게 오른쪽 그림처럼 까만 선을 그을 수 있지? (=거리를 계산할 수 있지?)라고 생각해보면, 시계열 안의 매 데이터 포인트를 비교할 때 ED처럼 자신과 동일한 인덱스인 친구만 비교하는 게 아니라, 가까운 친구들을 다 비교해서 제일 짧은 선을 그어준다는 것을 상상해볼 수 있습니다. 즉 ED는 3번째 데이터 포인트는 무조건 3번째랑 선을 긋지만, DTW는 10번째 데이터 포인트와 가장 가까운 9번째랑 그을 수 있다는 뜻입니다.

2개의 시계열 $x = x_1, \cdots, x_n$ 과 $y = y_1, \cdots, y_m$ 에 대해 그어진 선들의 집합을 와핑 경로 $\pi$ 라고 부르겠습니다(왜 ‘경로’인지는 잠시 후에 설명).

\[\pi = ((i_1, j_1),(i_2,j_2), \cdots, (i_K, j_K))\]

$\pi$ 의 각 원소는 두 시계열 사이 그은 까만 선이므로, 이를 구성하는 $i$ $(1 \le i \le n)$ 와 $j$ $(1 \le j \le m)$ 는 각 시계열의 몇번째 포인트를 그은 것인지를 알려주는 값입니다.

선을 그을 때는 다음과 같은 규칙이 있습니다.

1. 첫번째 포인트끼리와 마지막 포인트끼리는 무조건 그어야 한다.
   • $\pi_1 = (1,1)$ 이고 $\pi_{K} = (n, m)$
2. 두 포인트 이상을 뛰어넘어서 선을 그으면 안 되고(중간에 버려지는 포인트가 없게), 다음 선은 이번에 그은 포인트보다 인덱스가 작지 않게 그어야 한다(선이 크로스가 되지 않게).
   • $0 \le i_{k+1} - i_k \le 1$ 이고 $0 \le j_{k+1} - j_k \le 1$

다시 $\pi$ 의 각 원소는 선인데, 이 선의 길이가 바로 와핑 거리입니다. 비용(cost)라고도 합니다. 선을 따라 멀리 가야 할수록 비용이 높아지는 거죠.

우리의 목적은 이 모든 와핑 거리의 합(=와핑 경로 비용 = 모든 선의 길이의 총합)이 최소가 되는 $\pi$ 를 찾는 것 이고, 이때 와핑 경로 비용 값이 바로 DTW값이 됩니다.

(그림 출처)

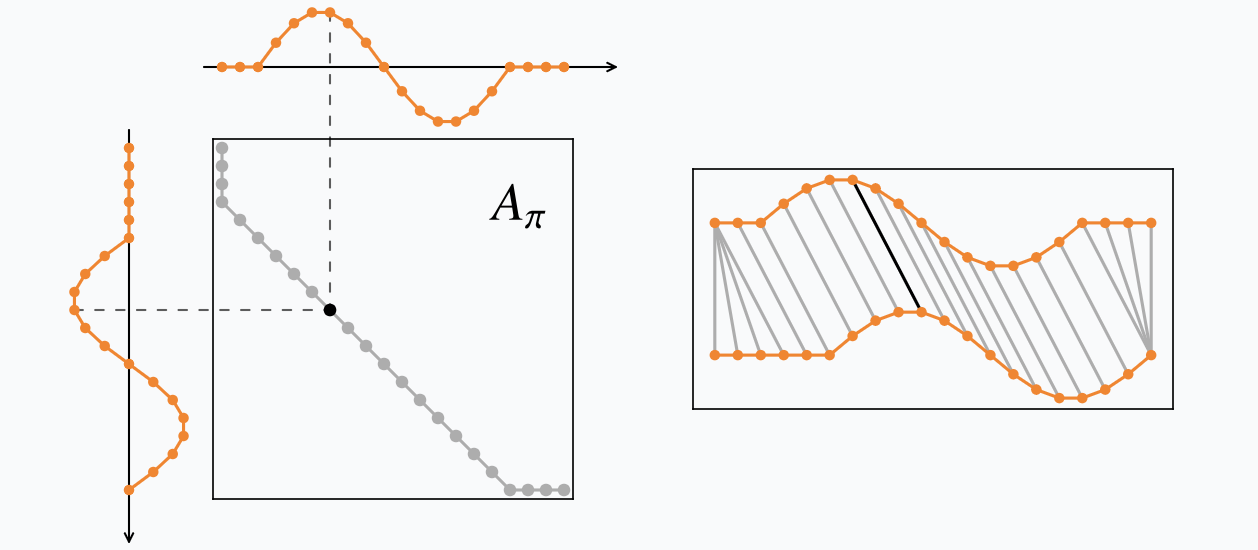
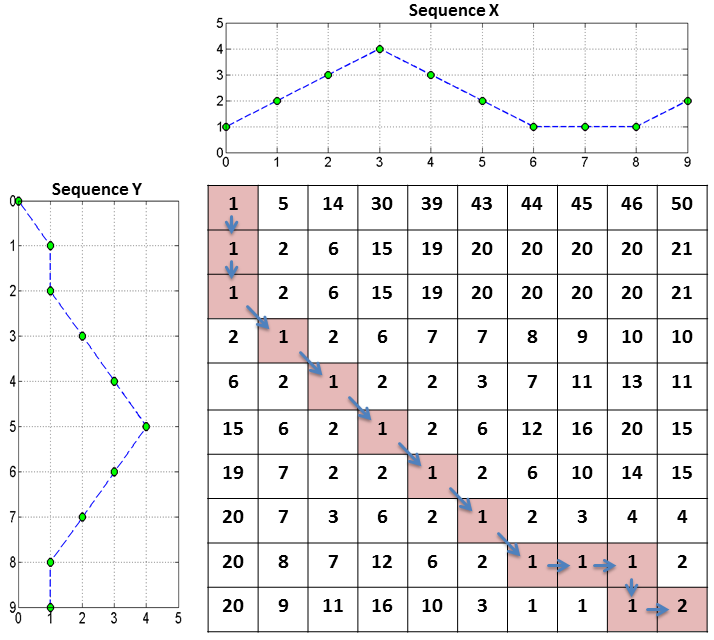
$\pi$ 를 왜 경로라고 부르냐면, 이 선의 집합을 다른 방식으로 생각해 봤을 때 시계열 2개의 길이인 $n$과 $m$만큼 행과 열의 개수를 가지는 행렬로 그려볼 수 있습니다. 이 행렬 $A_{ij}$는 만약 $(i,j)$가 $\pi$ 안에 있으면($x_i$와 $y_j$끼리 선이 그어졌으면) 회색으로 칠해주고, 그렇지 않으면 빈 값으로 채운다고 합시다. 그러면 위 그림처럼 행렬의 한쪽 끝에서 다른쪽 끝(규칙 1번에 따라 끝은 꼭 값이 있어야 합니다.)으로 가는 하나의 경로가 그려지는 걸 볼 수 있죠.

왜 굳이 행렬로 그려야 하는데? 라는 질문에 대한 답은 이 경로의 거리 합(비용)이 최소가 되는 걸 어떻게 찾을 거냐는 질문과 밀접한 관련이 있습니다.

(그림 출처)

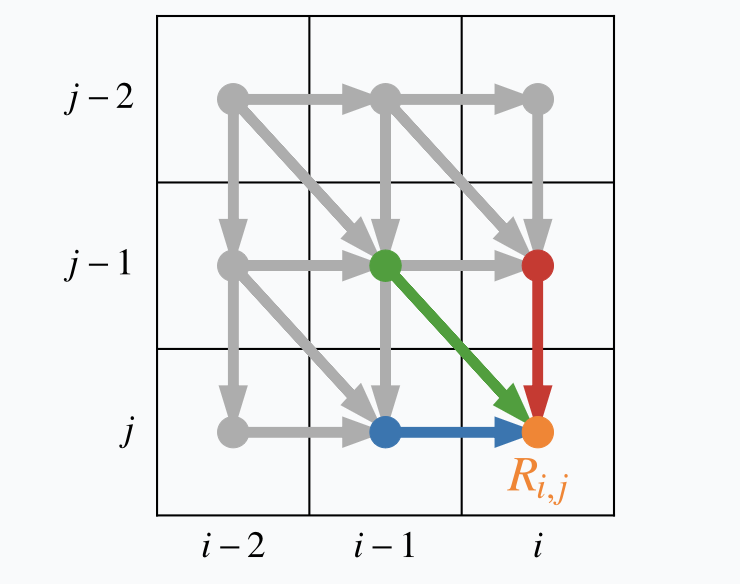
규칙 2번을 생각해보면, 그림에서 주황색 점에 도달하기 위한 직전 경로는 대각선 포함 인접한 칸들로부터 와야 하므로 빨간색/초록색/파란색 중 하나만 가능하다는 걸 알 수 있습니다. 즉 빨간색 점, 초록색 점 파란색 점 중 거기 도달하는 데 누적 비용이 가장 적었던 애를 골라주면 되겠죠. 이걸 매번 반복하면 최종 누적 비용이 가장 적은 칸들의 집합을 찾아낼 수 있을 겁니다.

각 칸마다 누적되는 거리의 값은 다음과 같이 써볼 수 있습니다. 즉 이번 칸의 거리와 위쪽/왼쪽/좌상단 칸의 누적 거리가 가장 작은 값을 더한 것입니다.

\(\text{SumD}(i,j) = \text{D}(x_i, y_j) + \min (\text{SumD}(x_{i-1}, y_{j-1}), \text{SumD}(x_i, y_{j-1}), \text{SumD}(x_{i-1}, y_j))\)

• SumD: 누적 거리, D: 거리
  

실제 예시를 볼까요?

• $X = [1, 2, 3, 4, 3, 2, 1, 1, 1, 2]$
• $Y = [0, 1, 1, 2, 3, 4, 3, 2, 1, 1]$

2개의 시계열은 언뜻 눈으로 봐도 1 2 3 4 3 2 1.. 하는 비슷한 패턴이 있습니다. 다만 이 패턴이 시작하는 시점이 약간 다르죠. 이 둘은 마침 길이가 똑같기 때문에 비교 차원에서 유클리디언 거리도 계산해볼 수 있습니다. 그 값은 4.47입니다.

DTW를 계산해보겠습니다. 나중에 제곱근을 취한다고 하고 $d(x_i,y_j)=(x_i-y_j)^2$로 우선 칸을 채우겠습니다. $\vert x_i - y_i\vert$ 로 해도 상관은 없지만요.

(그림 출처)

• 좌상단부터 시작!
  • $(1,1)$ : $d(x_1, y_1) = (1-0)^2 = 1$
  • $(2,1)$ : $d(x_2, y_1) + \min(1) = (2-0)^2 + 1 = 5$
  • $(1,2)$ : $d(x_1, y_2) + \min(1) = (1-1)^2 + 1 = 1$
  • $(2,2) : d(x_2, y_2) + \min(1,1,5) = (2-1)^2 + 1 = 2$
  • $\cdots$
  • $(10,10)$ : $d(x_{10}, y_{10}) + \min (1,1,2) = (2-1)^2 + 1 = 2$

하나하나 계산해보면 귀찮아서 그렇지 엄청 쉽습니다. 컴퓨터한테 시키면 더 쉽겠죠. 이렇게 모든 칸을 다 채우고, 마지막 칸 $(10,10)$으로부터 가장 근접한 작은 값을 고르는 방식으로 역추적하면 우리의 와핑 경로를 얻을 수 있습니다. 모든 칸은 누적 거리이므로, 마지막 칸 $(10,10)$의 값에 제곱근을 취한 값, 즉 $\sqrt{2} = 1.41$ 이 최종적인 누적 거리 = 누적 비용값 = DTW 값이 됩니다. 이 값은 유클리디언으로 구했던 거리의 약 1/3배 정도 작은 값입니다! 약간의 시간차가 발생하면서 비슷한 패턴을 보이는 두 시계열의 유사도를 DTW가 보다 더 잘 반영하고 있는 것을 확인할 수 있습니다.

그래서 어떻게 할까 클러스터링

제일 만만한 K-means

잘 알려진 클러스터링 기법들 중 가장 잘 알려진 K-means. 요약은 다음과 같습니다.

(그림 출처)

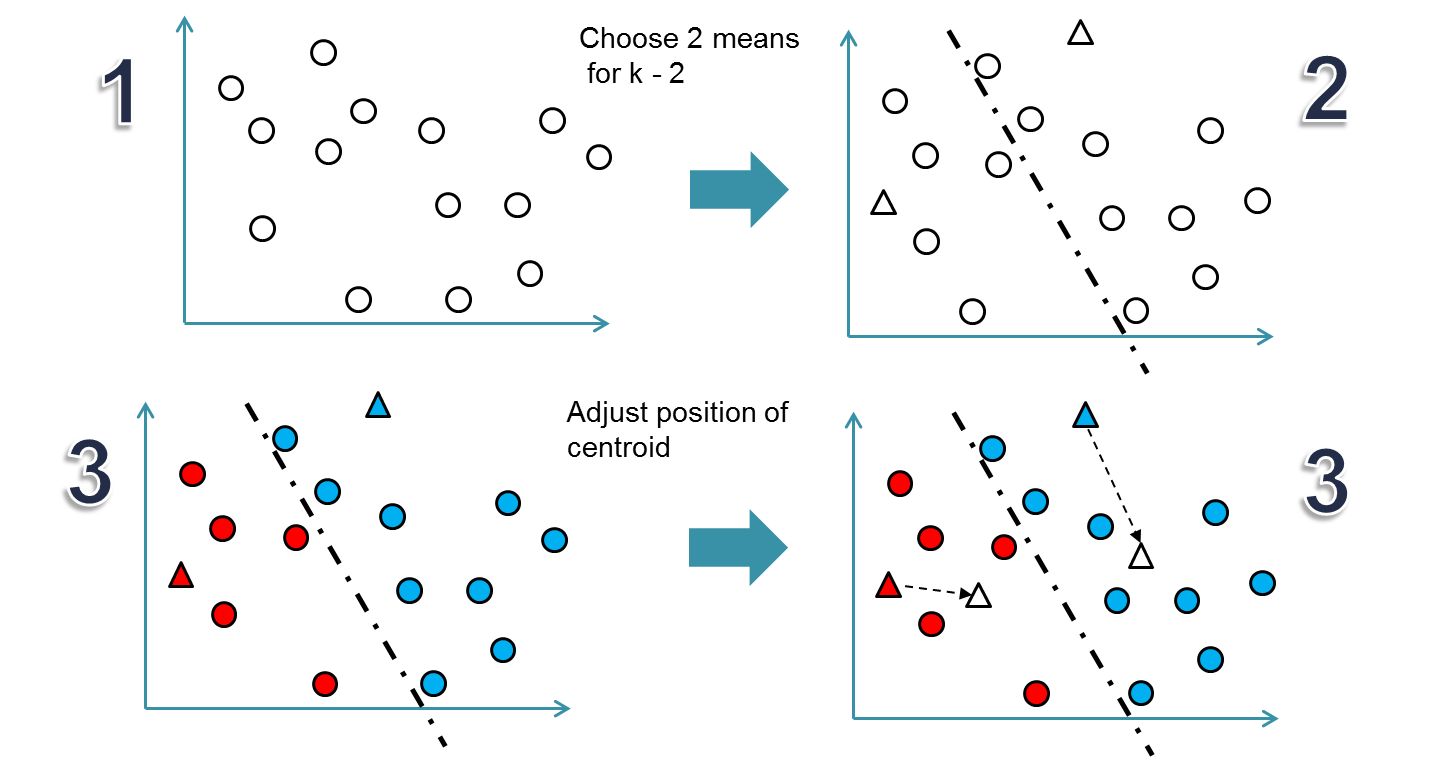
1. 군집 개수 k를 어떻게 할지 정하고 랜덤하게 중심(centroid) k개를 찍는다.
2. 모든 데이터를 가장 가까운(유사한) 중심으로 배정한다.
3. 배정된 데이터들의 평균을 새로운 중심이라고 한다.
4. 수렴할 때까지(정해진 군집이 바뀌지 않을 때까지) 2,3을 반복한다.

이때 2번에서 가까운(유사한) 을 판단할 때 유클리디언이 아닌 DTW를 사용하자! 라는 것인데요. 한가지 걸리는 점은 3번에서 평균은 어떻게 정하냐는 겁니다. 거리는 DTW로 판단하면서 평균은 그냥 산술평균 내? 일단 길이가 다르면 할 수 없다는 건 둘째치고, 위의 예시처럼 lag가 발생하는 경우 평균이 제대로 되지 않을까(DTW 필요한 이유랑 동일) 하는 의구심이 생깁니다.

그래서 DTW 개념을 유지하면서 여러 시계열의 평균을 내는 방법인 DBA(Dynamic Time Warping Barycenter Averaging) 라는 친구가 등장했습니다(논문). DTW를 사용한 k-means는 3번 단계에서 이 방법을 사용합니다.

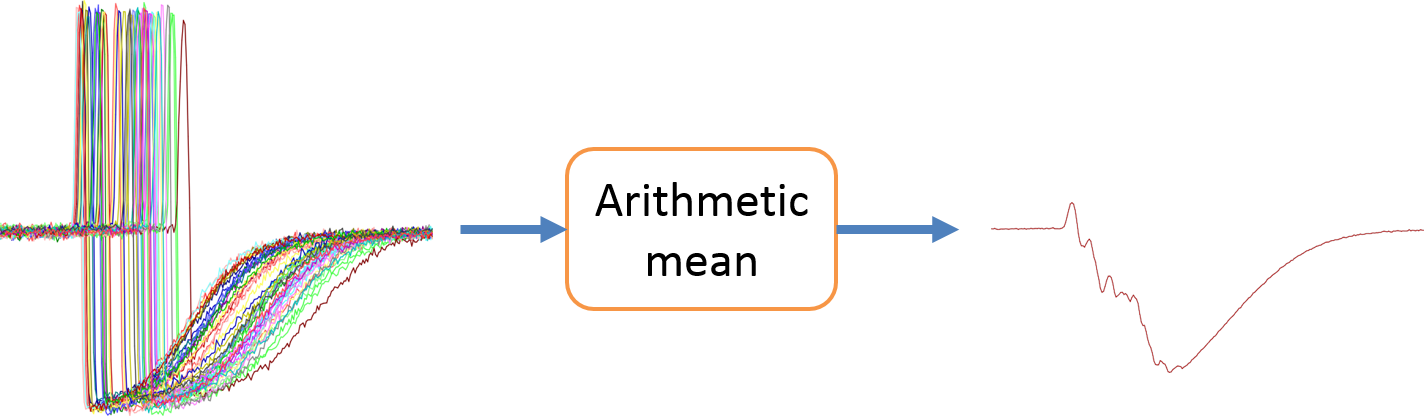
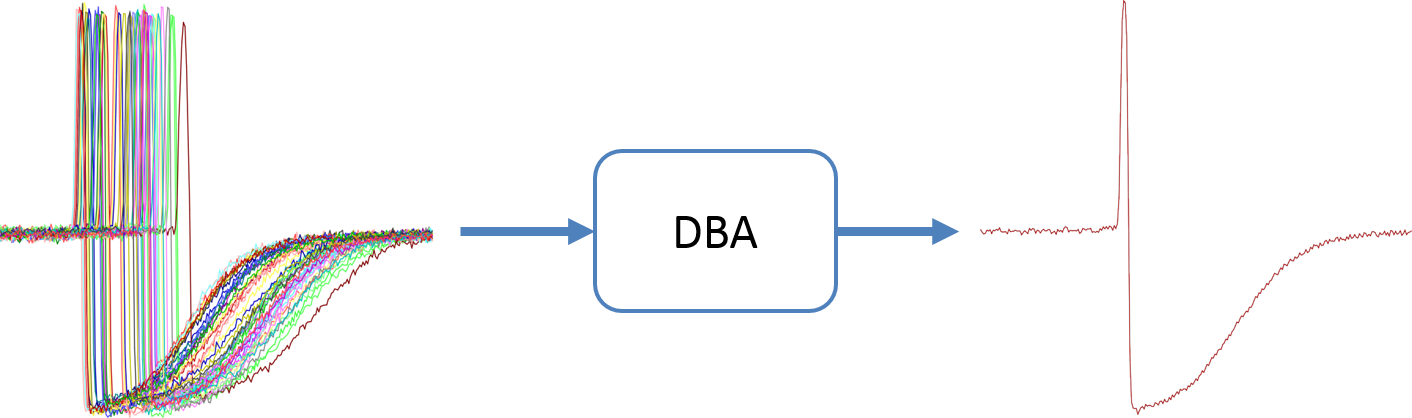한눈에 보는 그냥 평균과 DBA의 비교 (그림 출처)

이제 실제로 해봅시다.

import numpy as np
import matplotlib.pyplot as plt
from tslearn.clustering import TimeSeriesKMeans
from tslearn.datasets import CachedDatasets
from tslearn.preprocessing import TimeSeriesScalerMeanVariance, TimeSeriesResampler
import time #시간 측정을 위해

💭…라이브러리 임포트…💭

n = 100
m = 100
c_cnt = 4
seed = 0

np.random.seed(seed)
X_train, y_train, X_test, y_test = CachedDatasets().load_dataset("Trace")
X_train = X_train[y_train < c_cnt+1]
np.random.shuffle(X_train)
X_train = TimeSeriesScalerMeanVariance().fit_transform(X_train[:n])
X_train = TimeSeriesResampler(sz=m).fit_transform(X_train)
sz = X_train.shape[1]

시계열 분석을 위한 라이브러리 tslearn 에서 제공하는 클러스터링을 위해 쓸 수 있는 샘플 데이터입니다. 시계열 개수(n)는 100개고 각 시계열의 길이(m)도 100으로 맞춰줬고, 라벨은 3개만 가져왔습니다.

st = time.time() 

dba_kmeans = TimeSeriesKMeans(n_clusters=3, n_init=2, metric="dtw", verbose=True, max_iter_barycenter=10, random_state=seed)

y_pred = dba_kmeans.fit_predict(X_train)

print(f"{time.time()-st:.4f} sec")

k-means는 k가 몇인지를 설정해줘야 합니다 (n_clusters). metric 이라는 파라미터에 dtw 를 넣어서, dtw로 거리를 계산하도록 합니다. 파라미터들의 자세한 설명은 문서를 참고해주시면 됩니다.

시간은 7.1초 걸렸습니다.

결과는 다음과 같이 시각화를 해볼 수 있습니다.

for yi in range(3):
    plt.subplot(3, 3, 4 + yi)
    for xx in X_train[y_pred == yi]:
        plt.plot(xx.ravel(), "k-", alpha=.2)
    plt.xlim(0, sz)
    plt.ylim(-4, 4)
    plt.text(0.55, 0.85,'Cluster %d' % (yi + 1), transform=plt.gca().transAxes)
    if yi == 1:
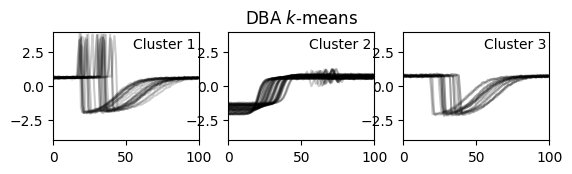
        plt.title("DBA $k$-means")

찐 라벨대로 아주 예쁘게 나눠졌습니다. 뭐 잘 될 수밖에 없는 게 tslearn 패키지의 dba k-means 예제 데이터니까 놀랍진 않습니다.

다만 저는 여기서 한 가지가 걸립니다. 뭐냐면 시간이요. 이거 사이즈가 100개짜리 시계열 100개였다는 걸 생각해봅시다. 이런 작은 사이즈의 샘플 데이터인데 7초나 걸린다고? 데이터 커지면 얼마나 걸리려고?

좀 느린 것 같은데 다른 방법 없나 (DBSCAN, Hierarchical Clustering)

왜 느린지를 생각해보면 k-means 작동 방식 상, 중심(centroid)을 정할 때마다 자꾸 거리 계산을 해야 하는 거예요. 이번 중심이랑 거리 계산해서 가까운 데다가 전체 데이터 재배정하고, 다시 그거 평균내서(DBA) 새로운 중심 정하고, 그럼 또 거리 계산해서…(수렴까지 반복)

이때 이렇게 하지 않고 이미 계산된 distance matrix만 있으면 그것만 가지고 돌아가는 다른 종류의 클러스터링 기법들이 있다는 사실이 떠올랐습니다. 바로 1) 밀도 기반 클러스터링인 DBSCAN과 2) 계층적 클러스터링입니다.

잠깐 리마인드해보면,

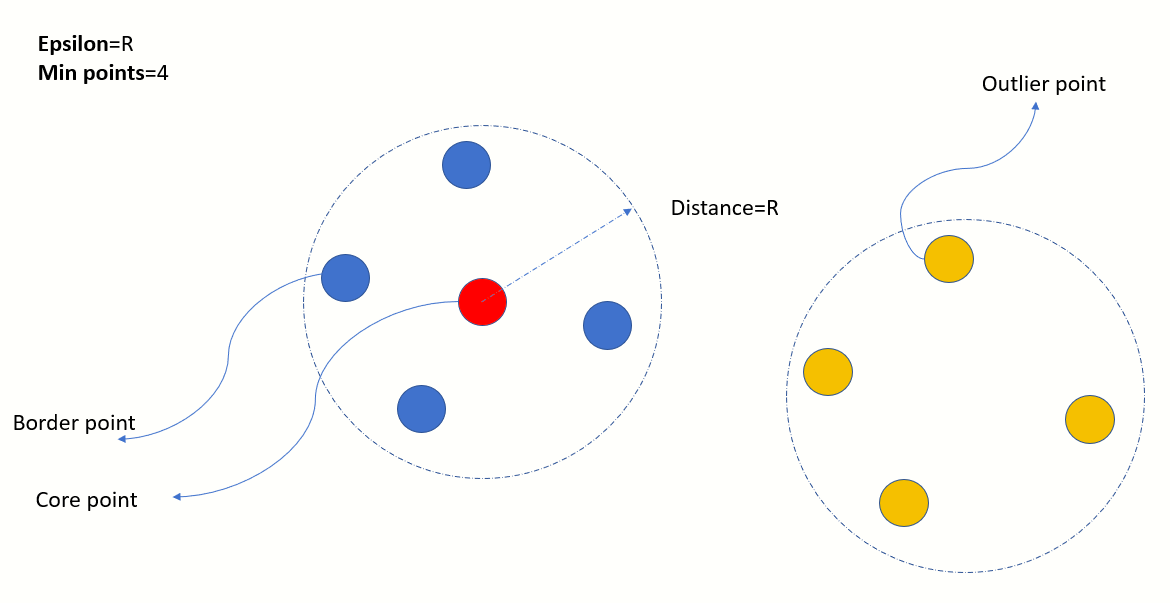
• Density-based Clustering (DBSCAN)
  • 이정도 가까워야 같은 군집이라고 볼 수 있다 라고 하는 반경(eps)값을 정하고, 그 반경보다 가까운 (더 촘촘한 밀도로) 연결된 군집으로 데이터들을 배정하고 그보다 멀리 있는 애들은 버리는 방식
    • (그림 출처)
  • 자세한 내용은 제가 작성한 다른 글 참고!
    • DBSCAN 이해하기
• Hierarchical Clustering
  • 거리가 가까운 순서대로 계층적으로 데이터들을 묶어나가는 방식
    • 다음과 같은 덴드로그램을 그리고, 적정한 수준에서 잘라서 군집을 형성
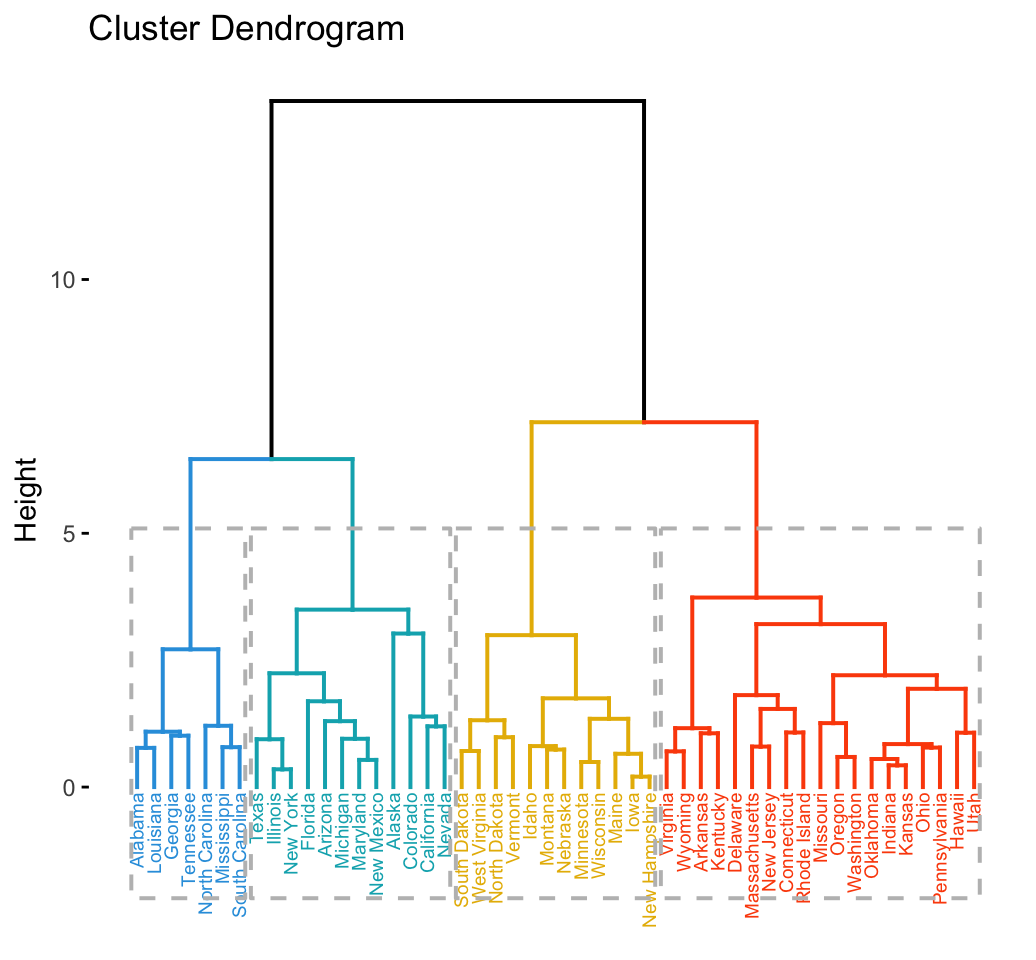    • (그림 출처)
  • 이 방식은 원래 거리(유사도) 행렬을 계산하고 시작함!

그러면 진짜 얘네가 더 빠를지 해봅시다.

from dtaidistance import dtw
from sklearn.cluster import AgglomerativeClustering
from sklearn.cluster import DBSCAN

💭…라이브러리 임포트…💭

st = time.time() 

ds = dtw.distance_matrix_fast(X_train.reshape(m, n))
ds[ds==np.inf] = 0
ds += ds.T  

dbscan = DBSCAN(metric='precomputed',eps=1.3)
dbscan.fit(ds)

print(f"{time.time()-st:.4f} sec")

앞부분은 dtaidistance 라는 라이브러리에서 제공하는 dtw를 통해 DTW를 계산해서 matrix를 얻습니다. distance_matrix_fast 는 메모리 절약을 위해 하삼각 부분은 inf 값이 들어갔고 상삼각 부분에만 거리 값을 넣은 행렬을 뱉어주는데요. (거리 행렬이니 (2,1) 랑 (1,2)는 어차피 값이 같으니까 (2,1)에만 값을 넣고 (1,2)은 비워놓는단 소리) 우리가 사용할 때는 full matrix가 필요해서, inf값을 0으로 바꾼 담에 이 행렬을 전치해서 더해줬습니다.

sklearn의 DBSCAN은 metric 이라는 파라미터에 precomputed 를 통해 계산된 distance matrix를 인풋으로 받을 수 있게 구현되어 있습니다. 즉 아까 k-means 때처럼 군집화할 데이터를 넣는 게 아니라 그걸로 계산한 거리 행렬을 넣는 겁니다. 파라미터 min_samples는 지정 안 했고, eps는 적당히 맞춰 줬습니다. 감으로.. 느낌대로.. (k-means가 k 모르면 노답인 것처럼 DBSCAN은 eps 잘못 맞추면 노답인데 전 지금 걸리는 시간이 더 궁금하거든요)

아무튼 얼마 걸렸냐면, 0.8초 걸렸습니다! 역시 훨씬 빠르네요.

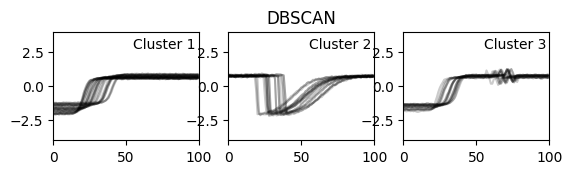
시각화해 보면, k-means의 결과랑 살짝 다르게 나왔죠. DBSCAN은 정해진 eps보다 거리가 멀면 noise로 분류해버립니다. K-means의 2번 군집을 2개의 군집(1, 3번 군집)으로 나눠버렸고, K-means의 1번 군집을(3번 군집이랑 비슷한데 위로 삐죽 솟은 패턴이 있는 애들)은 노이즈로 취급돼서 날아갔어요. 다시 말하지만 DBA k-means 샘플 데이터라서 거기서 최적의 결과가 나오는 건 어쩔 수 없을 것 같아요.

다음은 계층적 클러스터링입니다.

st = time.time()

ds = dtw.distance_matrix_fast(X_train.reshape(m, n))
ds[ds==np.inf] = 0
ds += ds.T

agglom = AgglomerativeClustering(metric='precomputed',linkage='complete', n_clusters = 3)
agglom.fit(ds)

print(f"{time.time()-st:.4f} sec") 

앞부분은 DBSCAN과 똑같고요. sklearn의 AgglomerativeClustering의 metric 라는 파라미터에 precomputed 를 넣어줍니다. 예전에는 affinity라는 파라미터였어서(최신 버전에서는 deprecated됨) 버전에 따라 affinity를 써야 할 수도 있습니다. 필수는 아니지만 이 기법도 k-means처럼 n_clusters를 지정해줄 수 있구요. 지정하지 않을 경우 군집이 2개가 나오길래(비슷한 라벨2과 3을 합쳐버리더라구요) 저는 이미 정답을 알고 있으므로 3개로 해줬습니다. 주의할 건 linkage 파라미터의 디폴트인 ward 는 유클리디언 거리에만 쓸 수 있다고 에러메시지가 뜹니다.

시간은 0.4초 걸렸습니다!

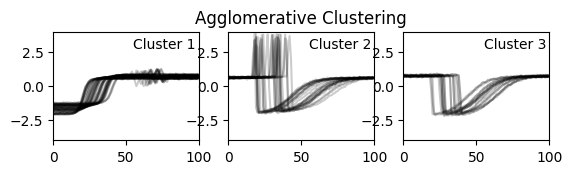
K-means와 거의 동일한 결과이며 약 17.5배 빠릅니다. 이 케이스에 한해서는 이걸 놔두고 k-means 써야 할 이유는 잘 모르겠긴 하네요.

이렇게 DTW와 쓸 수 있는 3가지 클러스터링 기법을 비교해봤습니다. 실제로 사용할 때는 데이터 사이즈도 더 클 것이고, 라벨이 없고, 노이즈도 더 많아서 생각만큼 정해진 군집으로 딱딱 떨어지지 않는 환경일 겁니다(이 샘플 데이터처럼 예쁘게 나눠질 리 없고, 라벨이란 게 있었으면 애초에 클러스터링을 안 쓰겠죠). 그러니 각 방식을 썼을 때의 비용(소요시간)과 평가 결과(시각화해보면서 정성적인 판단 or 실루엣 계수 등의 메트릭) 를 잘 비교해보면서 어떤 것을 쓸지 결정해야겠습니다.

---

참고한 글들

• An introduction to Dynamic Time Warping
• Time Series Similarity Using Dynamic Time Warping -Explained