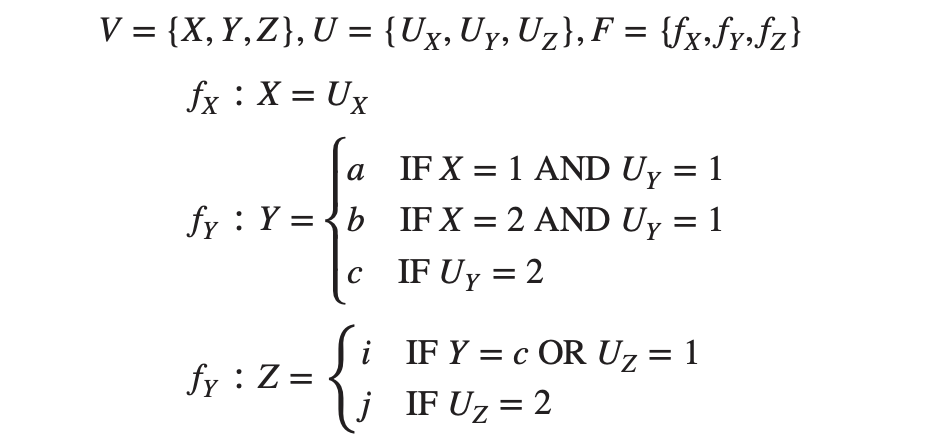인과 추론 2. 그래프와 확률

이 글은 Causal Inference in Statistics: A Primer의 2장과 3장 내용을 기반으로 작성하였습니다. 읽기 전에 독립과 조건부독립에 대한 개념과 그래프의 기본 구조 개념 이해가 필요합니다!

구조적 인과 모델 (Structural Causal Model)

인과와 관련된 질문에 답을 하려면, 주어진 데이터를 설명하는 인과 모델을 구성해야 합니다. 구조적 인과 모델(Structural Casual Model)이란 변수들 간의 인과 관계를 구조적인 식으로 나타낸 것입니다. 즉 변수들과 변수들 간 관계를 설명하는 함수로 구성되어 있습니다. Y라는 변수가 X에 값을 할당하는 어떤 식(함수) 안에 등장할 경우 Y를 X의 직접적 원인(direct cause) 이라고 보겠습니다. 즉 $X = Y + 2$라는 함수가 우리의 모델이라면, 우리 모델은 $Y$가 $X$의 원인이라고 주장하는 것이라고 보면 됩니다.

구성 요소를 자세히 살펴보면:

• $U$ : 외생(exogenous) 변수, 모델 밖에서 그 값이 결정되는 변수들의 집합
• $V$: 내생(endogenous) 변수, 모델 내에서 다른 변수들에 의해 설명되는 집합
• $f$ : 모델 내 다른 변수들에 따라 V에 속한 변수들의 값을 결정하는 함수 집합

모든 SCM은 그래프로 표현될 수 있습니다. $U$와 $V$에 속한 변수들을 노드로 하고 $f$의 함수들을 엣지라고 생각하는 것입니다. $Y$가 $X$의 직접적 원일일 경우 Y -> X 이렇게 $X$를 $Y$의 자식 노드로 그리게 되면, 익숙한 방향성 있는 비순환 그래프(DAG) 의 모습으로 그려질 것입니다. 외생 변수의 경우 모델 내에서 설명하지 않는 변수이므로, 어느 노드의 자식도 아닌 루트 노드여야 할 것입니다.

예를 들면 직원들의 월급($Z$), 교육 수준($X$), 경력($Y$)이 있을 때,

• SCM으로 표현하기 :
  • $U = {X, Y}$, $V = {Z}$, $F = {f_z}$
  • $f_z: Z = 2X +3Y$
• 그래프로 표현하기 :

인과 모델에서 그래프를 사용하는 이유

그래프를 쓰는 건 분명 완전하게 기술된 SCM보다는 정보가 부족합니다. 어떤 변수가 어떤 변수의 원인인지는 알 수 있지만, 뭐가 더 강하게 영향을 미치는지, 어떤 방식으로 미치는지는 알 수 없죠.

그럼 왜 그래프를 쓸까요?

• 인과관계에 대해 사실 수치적으로 규명할 수 있는 경우는 드물고 대부분 질적 관계만 발견해낼 수 있기 때문에
• 직관적인 이해에 도움이 되기 때문에
• 변수들 간 결합분포(joint distribution)를 매우 효율적으로 표현할 수 있게 해 주기 때문에

마지막 이유가 가장 중요합니다. 그래프만 보면, 두 변수간의 수치적인 관계를 정확히 모를 때에도 곱 분해(product decomposition)를 통해 결합 분포의 확률을 계산할 수 있습니다. 이게 무슨 말인지 살짝 살펴볼게요.

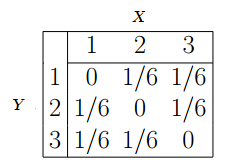
결합 확률 분포의 개념을 처음 배우는 사람은 다음과 같은 표를 꼭 마주치게 됩니다.

위 표는 $X$와 $Y$가 동시에 각각 어떤 값을 취할 때의 확률을 알려주고 있습니다. 그게 바로 그 두 변수의 결합 확률 분포이고요, 위 표를 구하기만 한다면 우리는 $X$, $Y$의 가능한 모든 값에 대해, 예를 들면 $X$는 1인 동시에 $Y$는 3일 확률은 무엇인가? 라는 질문에 대답할 수 있게 됩니다. 구하기만 한다면요.

하지만 이 표에서 금방 알 수 있는 점은 이 표에선 변수가 2개 뿐이고, 그 2개는 각각 1, 2, 3의 값만 취한다는 점이죠. 다른 모델, 조금 더 변수가 많고 복잡한 모델에서는 이런 식으로 모든 값의 쌍을 구하는 게 쉽지 않을 것입니다. 게다가 대부분 우리가 풀어야 하는 문제는 실제 확률 분포를 구한다기보다는 적당한 크기의 샘플 데이터를 가지고 추정을 하는 것인데, 3개 값을 취할 수 있는 변수가 4개 있다고 한다면 이것만 해도 81개의 확률값을 추정해야 합니다. 샘플이 모자라기 십상입니다.

여개서 곱 분해의 법칙을 한번 봅시다.

• (말로) 모든 비순환(acyclic) 그래프에서 변수들의 결합 확률 분포는 그래프 내 모든 가족 관계에 대해 부모 변수에 대한 자식 변수의 조건부 확률을 곱한 것으로 나타낼 수 있다.
• (식으로) $P(x_1, x_2, \cdots, x_n) = \prod_{i=1} P(x_i \vert pa_{i})$
  • $pa_i$는 변수 $X_i$의 부모 노드들을 뜻함

간단히 말하면, X → Y → Z 형태의 그래프가 있을 때 결합확률 분포는 $P(X=x, Y=y, Z=z) = P(X=x)P(Y=y \vert X = x)P(Z=z \vert Y= y)$ 입니다. 변수가 많아지면 많아질수록, 저 테이블을 하나하나 다 만드는 것보다 훨씬 간단해집니다. 즉, 모든 쌍에 대해 확률값을 다 구하는 게 아니라 그보다 더 작은 조건부분포의 테이블을 구해서 적절한 값을 곱하기만 하면 됩니다! 모델이 커질수록 자원을 효율적으로 사용할 수 있고, 굉장히 많은 변수들을 작은 데이터셋으로 추정해야 하는 문제를 피할 수 있습니다.

한마디로, 고차원의 추정 문제를 저차원의 확률 분포 문제로 바꿀 수 있다는 점이 그래프식 접근의 가장 큰 이점입니다.

이어서 인과 그래프에서 어떤 기본적인 형태들이 있고 각 형태들에서 독립/조건부 독립 정보를 어떻게 알아낼 수 있는지 알아 봅시다.

인과 모델의 그래프 형태들과 확률 정보

사슬 (chain)

연쇄적으로 하나의 변수가 다른 변수의 원인이고, 또 그 변수가 다른 변수의 원인인 경우의 그래프 형태를 사슬 형태라고 부릅니다. 이렇게 생겼습니다. 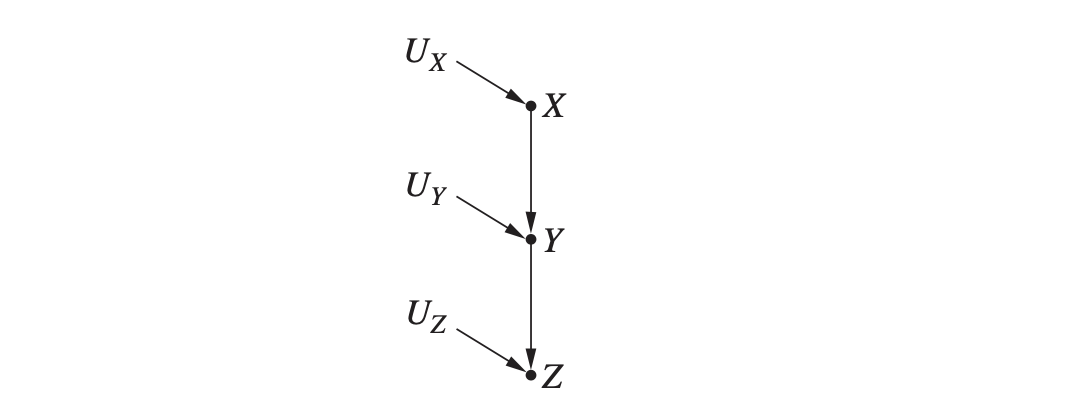실제로 인과 관계를 설명하는 방정식이 어떻든 사슬 형태의 그래프라면 다음이 성립합니다.

1. $Z$와 $Y$는 독립이 아니다.
   • 어떤 $z$ 와 $y$에 대해 $P( Z=z \vert Y = y) \neq P (Z = z)$ 가 성립한다.
2. $Y$와 $X$는 독립이 아니다.
   • 어떤 $x$와 $y$에 대해 $P( Z=z \vert Y = y) \neq P (Z = z)$ 가 성립한다.
3. $Z$와 $X$는 독립이 아닐 가능성이 크다.
   • 어떤 $x$와 $y$에 대해 $P( Z=z \vert X = x) \neq P (Z = z)$ 가 성립할 가능성이 크다.
   • “가능성이 크다”고 굳이 표현하는 것은 대부분의 경우 독립이 아닌데, 이상하게 독립인 케이스가 드물게 존재한다는 뜻. 아래와 같은 경우를 비전이 의존성(intransitive dependency)이라고 한다. 잘 살펴보면 $X$는 $Y$의 원인이 맞고 $Y$는 $Z$의 원인이 맞는데 어떤 경우에도 $X$가 $Z$의 값에 영향을 못 준다! 🤔
4. $Z$와 $X$는 $Y$에 대해 조건부 독립이다.
   • 모든 $x$ , $y$ , $z$ 에 대해 $P( Z=z \vert X = x, Y = y) = P (Z = z \vert Y = y)$ 가 성립한다.

SCM 그래프에서 한 변수가 다른 변수의 원인일 경우, 즉 방향성 엣지로 연결될 경우 두 변수는 독립이 아닙니다. 3번과 4번에서 $Z$와 $X$가 직접 엣지로 연결된 것은 아니지만 이러한 후손 노드 관계도 소수의 케이스를 빼고 대부분 독립이 아닌 이유는, 해당 구조가 $X$의 값이 변함에 따라 $Y$의 값도 변하고 $Y$의 값이 변함에 따라 $Z$도 변한다고 가정하기 때문입니다. 그러나 이러한 구조에서 중간 노드 $Y$를 하나의 값으로 고정할 경우, $Z$는 오직 $U_Z$의 영향만 받고 $X$의 변화와는 무관하게 됩니다(조건부독립).

분기 (fork)

분기 형태는 하나의 변수가 다른 두 변수의 공통적인 원인인 경우입니다.

예를 들어 어떤 도시의 온도($X$)와 아이스크림의 판매량($Y$), 그리고 폭력 범죄의 사건 수($Z$)를 생각해 봅시다. 온도는 뒤의 2가지 변수에 공통적으로 영향을 미칩니다. 세 변수 사이에는 다음과 같은 구조의 인과 모델을 만들 수 있습니다.

$V = {X, Y, Z}, U = {U_X, U_Y, U_Z}, F = {f_X, f_Y, f_Z}$

• $f_X : X = U_X$
• $f_Y : Y= 4x + U_Y$
• $f_Z : Z = \frac{x}{10} + U_Z$

이걸 그래프로 표현하면: 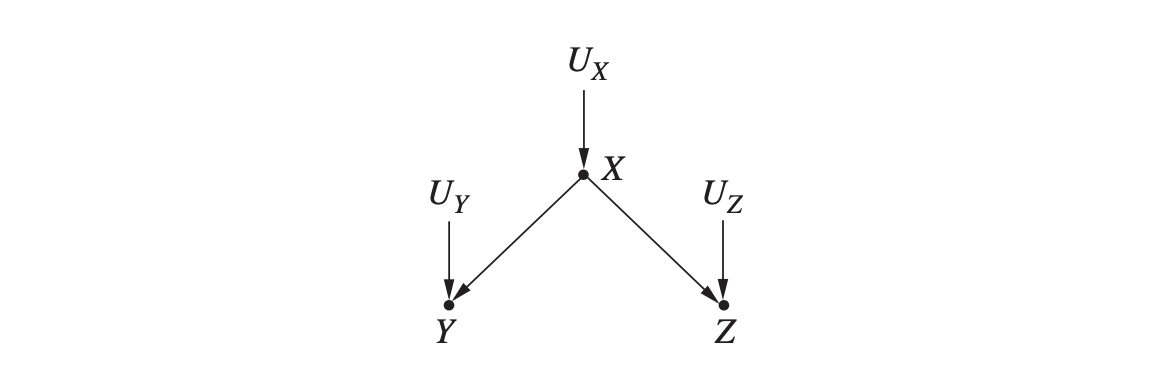분기 형태에서도 사슬 형태와 마찬가지로 다음이 성립합니다. 가장 중요한 부분은 X가 공통적 원인이 존재할 때 다른 두 변수는 그 공통 원인 변수에 대해 조건부 독립이라는 것입니다.

1. X와 Y는 독립이 아니다.
   • 어떤 $x$와 $y$에 대해 $P( X=x \vert Y = y) \neq P (X = x)$ 가 성립한다.
2. X와 Z는 독립이 아니다.
   • 어떤 $x$와 $z$에 대해 $P( X=x \vert Z = z) \neq P (X = x)$ 가 성립한다.
3. Z와 Y는 독립이 아닐 가능성이 크다.
   • 어떤 $z$와 $y$에 대해 $P( Z=z \vert Y = y) \neq P (Z = z)$ 가 성립할 가능성이 크다.
4. Y와 Z는 X에 대해 조건부 독립이다.
   • 모든 $x$ , $y$ , $z$ 에 대해 $P( Y=y \vert Z = z, X = x) \neq P (Y = y \vert X = x)$ 가 성립한다.

충돌 (collider)

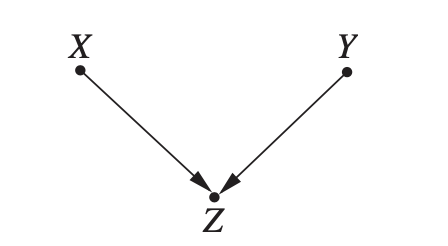
다음과 같이 두 개의 변수가 동시에 어떤 하나의 변수의 원인이 되는 경우 이 그래프를 충돌 형태라고 합니다.

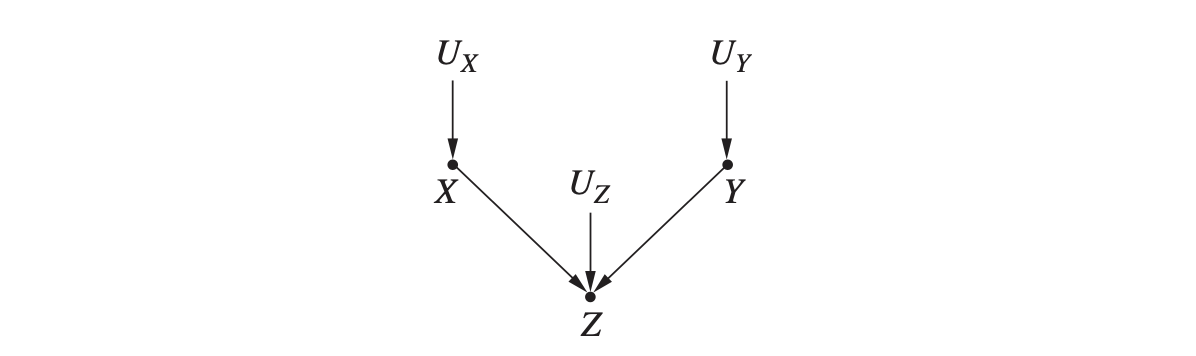이 형태에서 발견되는 변수들의 확률 정보는 이렇습니다.

1. X와 Z는 독립이 아니다.
   • 어떤 $x$와 $z$에 대해 $P( X=x \vert Z = z) \neq P (X = x)$ 가 성립한다.
2. Y와 Z는 독립이 아니다.
   • 어떤 $y$와 $z$에 대해 $P( Y=y \vert Z = z) \neq P (Y= y)$ 가 성립한다.
3. X와 Y는 독립이다.
   • 모든 $x$와 $y$에 대해 $P( X=x \vert Y = y) = P (X = x)$ 가 성립한다.
4. X와 Y는 Z에 대해 조건부로 독립이 아니다.
   • 어떤 $x$ , $y$ , $z$ 에 대해 $P( X=x \vert Y = y, Z = z) \neq P (X = x \vert Z = z)$ 가 성립한다.

1번과 2번의 경우 어떤 변수가 다른 변수의 원인일 때 그 두 변수는 독립이 아니라는 점에서 (사슬/분기 구조에서도 보았듯) 명확합니다. 3번의 경우에도 $X$와 $Y$는 오직 서로 독립이라고 가정되는 각각의 외생변수 $U_X$와 $U_Y$에게만 영향을 받으므로 둘은 독립입니다.

4번은 뭘까요? 가만히 냅두면 독립인 변수들이 그들의 공통적인 결과인 충돌 노드에 대해서는 조건부로 독립이 아니라는 말은 1~3번에 비하면 조금 덜 직관적으로 다가오는데요. 예를 들어 단순히 $Z = X+Y$라고 생각해 봅시다. $Z$에 대해 조건부라는 것은 $Z$의 값을 고정하겠다는 뜻이므로 $Z$가 10일 경우를 생각하면 $X$의 값이 바뀔 때, 예를 들어 $X$가 7이 될 경우 그에 맞춰서 $Y$는 3으로 정해져야 한다는 사실을 알 수 있습니다. 다른 예시로 어떤 대학에서 높은 학점 혹은 뛰어난 예술 실력을 지닌 사람에게만 장학금을 준다고 칩시다. 일반적으로 학점과 예술 실력은 별 상관이 없을 것입니다. 하지만 어떤 사람이 장학금을 받았다는 사실이 정해진 조건으로 주어진다면, 이 사람이 예술 실력이 없다는 사실은 그 자체로 그가 학점이 매우 높을 것이라는 사실을 말해 줍니다.

$d$-분리 ($d$-separation)

보통 인과 모델들은 위 그림들보단 더 복잡합니다. 변수들 사이에 1개 이상의 경로가 존재하고, 사슬/분기/충돌 형태들 여러 가지가 섞여 있기도 합니다. $d$-분리 는 어떤 복잡한 형태의 인과 모델 그래프에서 노드들 간의 독립 여부를 판단할 수 있게 해 주는 개념입니다.

간단하게 모든 두 변수의 관계는 다음 중 하나에 해당됩니다.

• $X$와 $Y$는 독립이 아니다 = $d$-연결 상태($d$-connected)이다 = $X$ 와 $Y$ 간 경로가 하나라도 차단되어 있지 않다.
• $X$와 $Y$는 독립이다 = $d$-분리 상태($d$-separated) 이다 = $X$와 $Y$ 간 모든 경로가 차단되어 있다.

경로 차단의 개념을 이해하기 위해, 독립이 아님 (dependency)를 그래프의 엣지를 파이프 삼아 흐르는 물이라고 생각해 봅시다. 즉 파이프가 차단되어 있어야 물이 흐르지 않습니다(=독립입니다). 그럼 어떤 노드가 파이프를 차단할 수 있을까요?

• 우리가 알아보고자 하는 것이 조건부 독립이 아니라 무조건 독립일 경우
  • 충돌 노드만 경로를 차단할 수 있다.
• 특정 변수 집합 $Z$에 대해 조건부 독립일 경우
  • $Z$ 중 하나의 변수 사슬의 중간 노드나 분기의 시작 노드일 경우 경로를 차단할 수 있다.
  • 충돌 노드이면서 $Z$ 중 하나가 아니고 그 후손도 $Z$ 에 속하지 않는 경우만 경로를 차단할 수 있다.
    • (충돌 노드가 조건으로 설정될 경우 그 원인 변수들이 조건부로 독립이 아니게 되기 때문!)

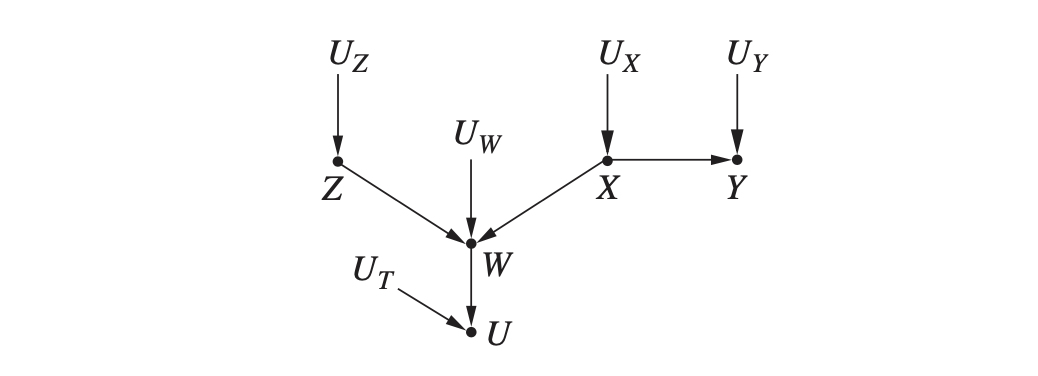
  예시로 다음과 같은 그래프에서 $Z$와 $Y$의 독립 여부를 살펴보고 싶다고 합시다. 이 문제는 $Z$에서 $Y$로 가는 경로를 차단할 수 있는지 없는지를 보는 것과 동일합니다.

• 조건부 노드를 사용하지 않을 경우 (Conditioning set : { } ), $Z$와 $Y$는 독립이다. ( $Z$ → $W$ ← $X$ 라는 충돌 노드가 경로를 차단한다.)
• $W$나 $U$가 조건부 노드가 될 경우 (Conditioning set : { W } or { U } ), $Z$와 $Y$는 독립이 아니다. ($W$ 또는 그 후손인 $U$는 충돌 노드이면서 조건부이기 때문에 경로를 차단하지 못한다.)
• $W$와 $X$가 조건부 노드가 될 경우 (Conditioning set : {W, X}), $Z$와 $Y$는 독립이다. ($W$는 경로를 차단하지 못하지만 분기의 시작 노드인 $X$는 조건부 노드이면 경로를 차단한다.)

인과 모델 테스트하기

지금까지 배운 개념들을 사용해서 주어진 인과 모델을 테스트하는 방법을 알아보겠습니다. 대충 흐름은 이렇습니다.

• 인과 모델/그래프 $G$가 있고, 데이터 $S$가 있다.
• $G$라는 그래프 하에 $S$가 생성되었을 것이라는 가설을 시험하고 싶다.
• $d$-분리 개념을 통해 변수들의 조건부 독립 관계를 얻어낸다. 즉 $G$가 적절한 모델이라면 변수 $A$와 변수 $B$는 변수 $C$에 대해 조건부 독립이어야 한다.
• 그러나 데이터 $S$를 가지고 확률을 추정했을 때 그 조건부 독립 관계가 맞지 않다면, $G$는 $S$를 적절히 설명하는 인과 모델이 아닌 것이다.

$d$-분리로 테스트하고자 하는 조건부 독립 관계를 추출해내는 것은 모델 전체에 대해 전역적으로 통계적 가설 검정을 하는 일반적인 테스트 방식에 비해 다음과 같은 이점을 지닙니다.

• 비모수적(nonparametric) 방식으로 변수들 간의 특정한 함수를 필요로 하지 않는다.
• 모델을 지역적으로만 테스트함으로써, 모델의 어느 부분이 틀렸는지 확인할 수 있게 한다.

예시로, 요렇게 생긴 모델이 있습니다.

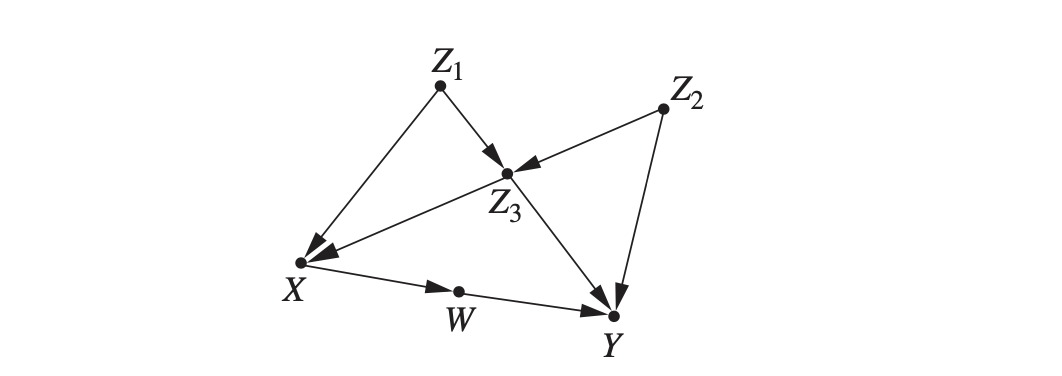이때 우리가 테스트하는 것은 전체 그래프가 아니라 $W$와 $Z_1$ 이 $X$에 대해 조건부 독립이라는 특정 $d$-분리 관계입니다. 이 그래프에서는 그 외에도 다른 $d$-분리 관계들을 찾아낼 수 있지만 일단 그것만 테스트 합니다. 그러기 위해서 주어진 데이터로 $X$와 $Z_1$로 $W$를 설명하는 회귀식을 만듭니다. 최적의 선 $w=r_X x + r_1z_1$ 를 찾았는데, $r_1$이 0이 아니라고 칩시다. 그러면 우리는 가정했던 조건부 독립이 아니라는 사실을 알 수 있고, 이 그래프가 틀렸다는 사실도 알 수 있겠죠. 이때 그냥 모델이 틀렸다 가 아니라 $W$와 $Z_1$ 이 $X$에 대해 조건부독립이 아니라는 점에서 틀렸다! 를 알 수 있다는 점이 중요합니다. 즉 $W$와 $Z_1$ 사이 차단되지 않는 어떤 경로가 있도록 모델을 수정해야 합니다. 만약 사람이 아니라 컴퓨터라면 이 과정을 반복해서 데이터셋과 모순되지 않는 조건부 독립 관계들을 가진 그래프의 집합들을 찾아낼 수 있을 것입니다.