신경망 기반 언어 모델의 약점: Stolen Probability Effect
단어 시퀀스에 확률을 부여하여 특정 시퀀스가 얼마나 발생할 확률이 높은지, 즉 “자연스러운” 언어 시퀀스인지를 판단하도록 학습시킨 모델을 언어 모델(Language model) 이라고 부릅니다. 이전에 통계 기반의 전통적인 언어 모델은 주로 학습 데이터에 계산하는 단어들을 카운팅하는, 즉 빈도를 통해 확률을 계산하는 식의 접근을 취했습니다. 이런 통계적 언어 모델은 학습 데이터에 등장하지 않는 시퀀스에 대처할 수 없고, 단어나 단어 시퀀스나 문장 간 유사도를 판단하기 어렵습니다. 신경망 기반의 언어 모델(Neural Network Language Model) 은 이러한 약점을 극복하는 것으로, A Neural Probabilistic Language Model (Bengio, 2003) 에서 처음 등장한 이후로 간단한 피드-포워드 신경망으로부터 LSTM, 최근의 트랜스포머 아키텍쳐까지 다양한 형태의 모델들로 발전해 왔습니다.
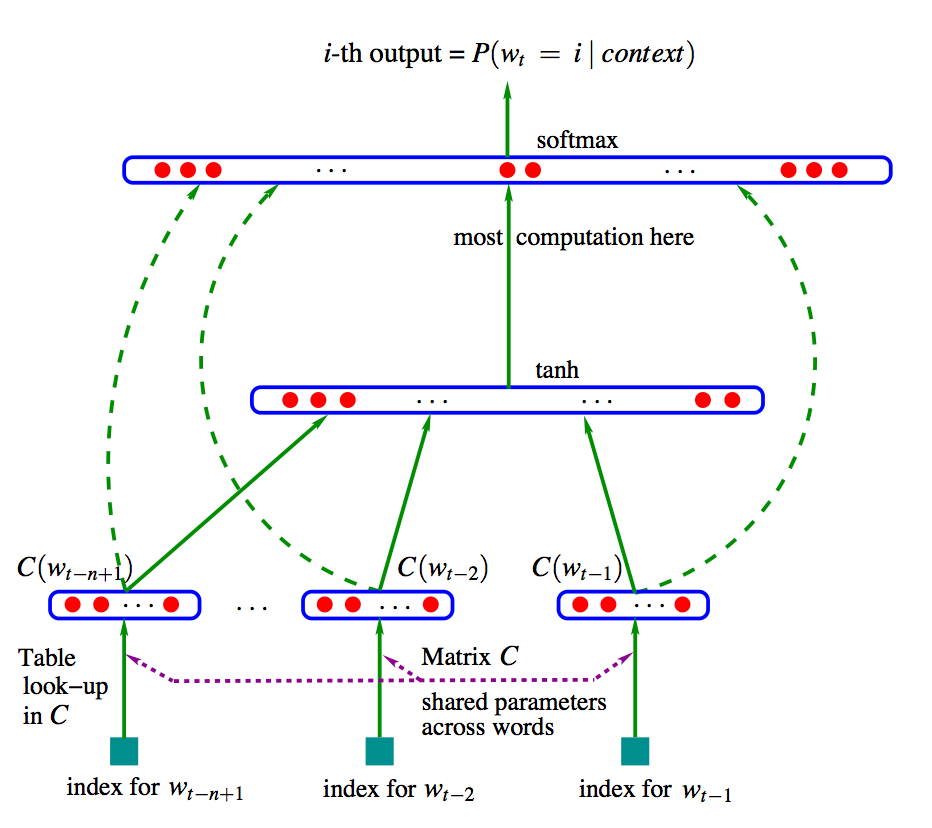
NNLM의 첫 등장인, 위 논문에서 제시된 신경망 기반 확률 언어 모델 (Neural Probabilistic Langauge Model)의 구조에 대해서 간단히 살펴보겠습니다.
신경망 기반 언어 모델은 단어 시퀀스가 주어졌을 때 다음 단어가 무엇인지 맞추도록 신경망을 학습합니다. 직전까지 등장한 n-1개 단어들로 다음 단어를 맞추는 n-gram 언어 모델이라고 할 수 있습니다. 문장 내 t번째 단어 $w_t$에 대해 모델은 다음음을 최대화해야 합니다. 주어진 단어들 다음에 실제로 등장하는 정답 단어가 등장할 조건부 확률이죠.
$P(w_t \vert w_{t-1}, \cdots, w_{t-n+1}) = \frac{\exp (y_{w_t})}{\sum_i \exp (y_i)}$
먼저 모델의 입력에 대해 알아봅시다. 우선 문장 내 t번째 단어에 대응하는 벡터 $x_t = C(w_t)$를 만듭니다. 이 $C$는 $\vert V \vert \times m$ 크기를 갖는 행렬이고 ($m$은 $x_t$의 차원 수), $w_t$ 에 해당하는 벡터를 참조(lookup) 한 형태입니다. 이 $C$의 원소값들은 처음에 랜덤으로 설정됩니다. ($*$ lookup = 행렬과 원핫벡터를 내적해서 얻습니다.) 예를 들어 파파존스 스파이시 이탈리안 피자 가 있고, 앞의 세 단어로 마지막 피자 를 예측한다고 하면, 파파존스 , 스파이시, 이탈리안 이 3개 단어의 인덱스를 확인해서 $C$에서 참조한 후 가져온 3개 벡터를 연결(concatenate)하면 입력 벡터 $\mathbb{x}$ 를 얻습니다($x = [ x_{파파존스}, x_{스파이시}, x_{이탈리안} ]$ ).
입력된 벡터는 순서대로 신경망의 입력층, 은닉층, 출력층을 거칩니다. 모델의 출력은 $\vert V \vert$ 차원(=어휘 사전 크기)의 스코어 벡터 $y_{w_t}$에 소프트맥스 함수를 적용한 확률 벡터인데, 스코어 벡터는 다음과 같이 계산됩니다.
$y_{w_t} = b + Wx + U \tanh (d+Hx)$
그리고 소프트맥스를 적용하여 확률 벡터를 얻고, 가장 높은 요소의 인덱스에 해당하는, 즉 등장할 확률이 가장 높은 단어가 실제 정답 단어인 피자 와 일치하도록 역전파합니다. 학습이 종료되고 최종적으로 얻은 $C$의 값들이 각 단어에 대한 $m$차원 임베딩이 됩니다.
Stolen Probability Effect
Stolen Probability: A Structural Weakness of Neural Language Models 는 이러한 NNLM에 구조적인 한계가 존재한다는 점을 지적한 최근의 연구입니다(ACL 2020). 내용은 간단하게 다음과 같습니다.
NNLM이 지난 몇 년 동안 여러 형태의 모델로 고도화되면서도 단 하나 바뀌지 않는게 있다면, 출력층에서의 소프트맥스 사용입니다. NNLM은 매우 고차원 공간에 형성된 단어 임베딩에 대해 예측 벡터를 내적함으로써 일종의 거리 메트릭을 만들고, 여기에 활성화 함수로 소프트맥스를 사용함으로써 확률 분포를 생성해 냅니다. 이 논문은 이런 벡터 내적 기반의 거리 메트릭이 NNLM의 귀납적 편향을 유발하고, 결론적으로 형성된 임베딩의 표현(expressiveness)의 한계를 가져온다는 것을 보여줍니다. 자세히는, 특정 단어들이 단순히 임베딩 공간에서의 상대적인 위치 때문에 다른 단어들의 확률을 “훔쳐오는” 현상이 발생한다는 것인데요. 이 논문은 이 현상을 도둑맞은 확률 효과로 명명하고, 이 문제가 어떤 케이스에서는 심각한 오류의 원인이 되기도 한다는 것을 보여줍니다.
이 현상의 핵심은 NNLM에서 특정 임베딩을 가진 단어는 어떤 맥락에서도 결코 높은 확률을 부여받을 수 없다는 것입니다.
그러기 위해서 임베딩 공간에서 벡터 노름과 확률의 관계를 살펴보겠습니다. NNLM에서 단어 $w_i$는 벡터 $x_i$로 임베딩되며, 맥락 $c$에 대해 $x_c = {x_i}_{i \in c}$를 신경망에 넣으면 예측 벡터 $h_t$가 생성되는 식입니다. 즉 NNLM은 단어 사전 $w_i$의 확률 분포를 만들어서, 특정 단어 시퀀스 $w_t$에 대해 예측하도록 학습을 하죠.
\[P(w_t=w_i|c)=\sigma (f(x_c, \theta_{NNLM})) = \frac{e^{z_{it}}} {\sum_v e^{z_{vt}}}\]이때 $\sigma$는 소프트맥스 함수고, $f$는 예측 벡터 $h$를 만드는 신경망 유닛이며, $\theta$는 신경망의 파라미터입니다. 즉 위 식은 맥락 $c$가 주어졌을 때 단어 시퀀스 $w_t$가 발생할 확률이죠. 이걸 뜯어보면, 예측 벡터와 단어 벡터에 대해 내적을 계산해서 로짓($z_{it}$)을 만들고, 그 로짓에 소프트맥스를 취한 것입니다. 이때 로짓은 다음과 같습니다.
\[z_{it} = x_i \cdot h_t^T + b_i = \Vert x_i \Vert \Vert h_t \Vert \cos(\theta_i) + b_i\](여기서 $\theta_i$는 $x_i$와 $h_t$ 사이의 각도입니다.)
내적 소프트맥스의 기본 방식은 단어 $w_i$ 의 확률이 다른 로짓 값들에 비해 $z_{it}$가 상대적으로 얼마나 크냐에 따라 할당된다는 것입니다. 위 식을 볼 때, 각도가 동일하다면 노름($\Vert x_i \Vert$)이 큰 단어가 확률이 커지겠죠. 즉 일반적으로 확률이 높은 단어 A와 그보다 낮은 단어 B가 있을 때 단어 임베딩의 노름과 예측 벡터 $h_t$와의 각도의 관계는 다음과 같이 표현됩니다.
\[\frac{\Vert x_A \Vert}{\Vert x_B \Vert} > \frac{\cos(\theta_B)}{\cos(\theta_A)}\]NNLM이 단어 벡터 노름이 퍼져 있는 임베딩 공간을 형성하더라도 예측 백터와의 각도는 그보다 더 좁은 범위로 한정되게 됩니다. 이에 따라 노름이 로짓 값을 결정하게 되고, 결론적으로는 확률도 결정하게 된다는 것입니다.
이제 본격적으로 임베딩 공간에서의 단어의 위치와 볼록 껍질(Convex hull)을 비교해 봅시다. 볼록 껍질이란 유클리디언 공간에서 다른 포인트들을 포함하는 볼록 다각형을 형성하는 가장 작은 포인트들의 집합을 뜻합니다. 관련하여 연구의 핵심 정리는 다음과 같습니다.
(단어 사전 $V$의 임베딩 ${x_i}$에서 $C$가 볼록 껍질이라고 할 때) 단어 $w_i$가 $C$ 안에 위치할 경우, 소프트맥스 함수를 사용하여 $w_i$ 에 할당되는 최대 확률 $P(w_i)$는 $C$ 위에 위치한 적어도 한 개의 단어에 할당된 확률 의해 bounded 된다.
(증명은 원 논문의 부록에 수록되어 있으며, 아래는 수치해석 부분만 설명합니다.)
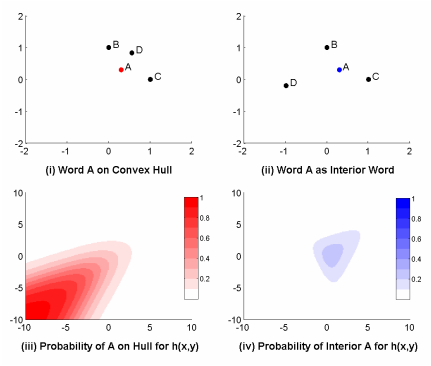2차원 유클리디언 공간에서 예시를 들어 봅시다. A라는 단어의 임베딩이 볼록 껍질 위에 위치할 때(좌)랑 안쪽에 위치할 때(우)를 비교해 볼게요. 내적 소프트맥스로 확률을 할당했을 때, A가 볼록 껍질 위에 위치하면 사분면의 좌하단으로 갈수록 확률이 높아져 거의 1(100%)까지 할당되는 것이 가능하지만, 안에 위치하면 볼록 껍질 위 다른 단어들(B, C, D)에 의해 한계가 생기는 것을 볼 수 있습니다. 이 현상을 볼록 껍질 위의 단어가 안의 단어의 확률을 “훔쳐온다”고 표현한 것이죠.
실험
이 연구에서 실험에 사용한 모델과 알고리즘은 다음과 같습니다.
- Wikitext-2 말뭉치에서 훈련된 AWD-LSTM 과 MoS(Mixture of Softmaxes) 모델 사용
- 볼록 껍질 탐지 알고리즘으로 Quickhull 사용 → 볼록 껍질 안(interior) 단어와 아닌(non-iterior) 단어로 모든 단어 임베딩을 분류
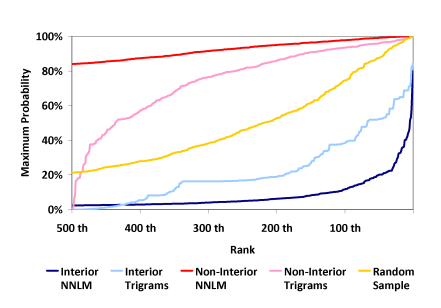
첫번째 그림은 볼록 껍질 안 단어들과 그렇지 않은 단어들, 그리고 랜덤으로 추출된 단어들에 대해 최대 확률을 계산하고, 상위 500 단어만 그림으로 그린 것입니다. 그리고 NPLM 이전의, 스무딩 기법을 사용한 전통적인 n-gram 확률 모델로 계산한 확률(“Trigrams”)도 같이 표기하였습니다. 내적 소프트맥스를 사용하지 않는 이전의 N-gram 모델은 볼록 껍질 안 단어들에 대해서도 꽤 높은 확률을 부여할 수 있는 반면[하늘색 선], NNLM 모델은 그 단어들에는 절대 높은 확률을 할당하지 못하는 것으로 보입니다[파란색 선]. 다른 단어들(non-interior)은 괜찮고요. 같은 단어들의 확률값을 평균낸 값을 보아도, 볼록 껍질 안 단어들의 최대 확률이 평균적으로 활씬 더 작은 것을 확인할 수 있습니다.
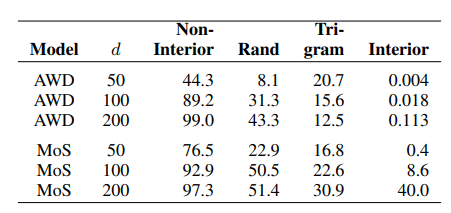
이 도둑맞은 확률 현상이 언어 모델의 성능에 미치는 영향은, NNLM을 N-gram과 앙상블했을 때 드러납니다. 논문은 MoS와 trigram 모델을 앙상블하여 PPL(Perplexity, 언어 모델의 성능을 평가하는 지표)이 훈련 데이터에서 34.8에서 33.6으로, 테스트 데이터에서 67.4에서 67.0으로 향상되는 것을 확인했다고 합니다. 또 볼록 껍질 내부(interior) 단어로만 한정해서 볼 경우 이 향상이 매우 극적이었다고 하는데, 훈련 데이터의 경우 700.0에서 157.2로, 테스트 데이터의 경우 645.6에서 306.7로 나아졌다고 합니다. 비록 전체로 봤을 때 PPL 차이는 그닥 크지 않지만, 적어도 NNLM 하에서 확률을 빼앗겼던 특정 단어들에 대해서는 이런 식으로 언어 모델을 보완할 수 있다는 점을 확인할 수 있었습니다.
이 연구에서 제시된 현상(stolen probability effect)은 잘 알려진 소프트맥스 병목(Breaking the Softmax Bottleneck: A High-Rank RNN Language Model, 2018) 과는 다른 이야기입니다. 이는 언어 모델을 행렬 분해 문제로 바꿔서, 소프트맥스 함수 사용으로 인해 모델의 표현력이 단어 임베딩 행렬의 랭크에 의해 한계가 생긴다는 것을 보여준 연구인데요. 그러나 도둑맞은 확률 효과에서 제시된 문제점은 임베딩 공간의 차원이 아닌 배치(arrangement)에 의해 생기는 것이고, 사실 차원이 크고 작음과는 관계가 없습니다. 그러나 차원이 증가함에 따라 볼록 껍질 내부 데이터에 부여되는 확률 질량 평균이 증가하기는 합니다. 즉 확률 도둑에도 한계가 있게 됩니다. 이는 차원이 올라가서 임베딩 공간에 여유 용량이 생길수록 모델의 자유도가 올라가기 때문에 자연스러운 현상입니다. 이 연구에서 사용한 wikitext-2 말뭉치는 상대적으로 작은 크기의 말뭉치고, 만약 훈련 데이터셋이 더 크다면 이 현상에도 차이가 있을 것이라고 하네요. 더 최근의 신경망 기반 언어 모델들에 적용한 결과도 궁금해집니다.