스펙트럴 클러스터링 이해하기
스펙트럴 클러스터링을 어떻게 하는지에 대한 글이며 써보기보다는 이해하기를 목적으로 적었습니다.
뭘까?
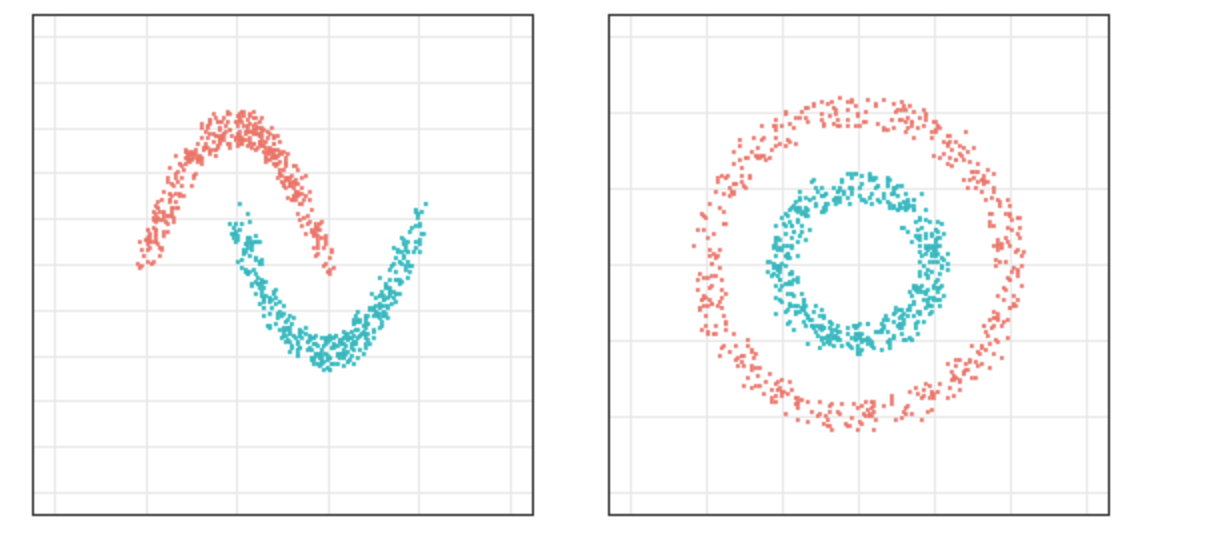
스펙트럴 클러스터링은 클러스터링, 즉 군집화 기법의 일종입니다. 클러스터링의 기본 목적은 주어진 라벨 없는 데이터에 대해 비슷한 것끼리 군집으로 묶어주는 것이죠. 비슷한 것들은 같은 군집에 속하고 다른 것들은 다른 군집에 속하도록 합니다.
그 중에서도 스펙트럴 클러스터링은 그래프 기반 클러스터링입니다. 그래프 기반이라는 것은 데이터들 간의 상대적인 관계나 연결을 가장 중요한 정보로 이용하겠다는 뜻입니다.
이것이 바로 가장 잘 알려진 클러스터링 기법 중 하나인 K-평균 클러스터링과의 큰 차이점인데요, K-평균 클러스터링은 유클리디언 공간 위의 데이터의 값들 자체의 거리(유사도)를 기반으로, 군집의 중심을 정하고 그 중심에 가깝게 데이터들을 배정해가는 방식으로 군집을 찾아냅니다. 반면 그래프 기반으로 접근할 경우 데이터들의 절대적 위치가 중요한 것이 아니라 그들이 연결되어 있는지(연결되어 있다면 얼마나 가까이 강하게 연결되어 있는지)를 보고 같은 군집인지 아닌지를 판단하게 됩니다.
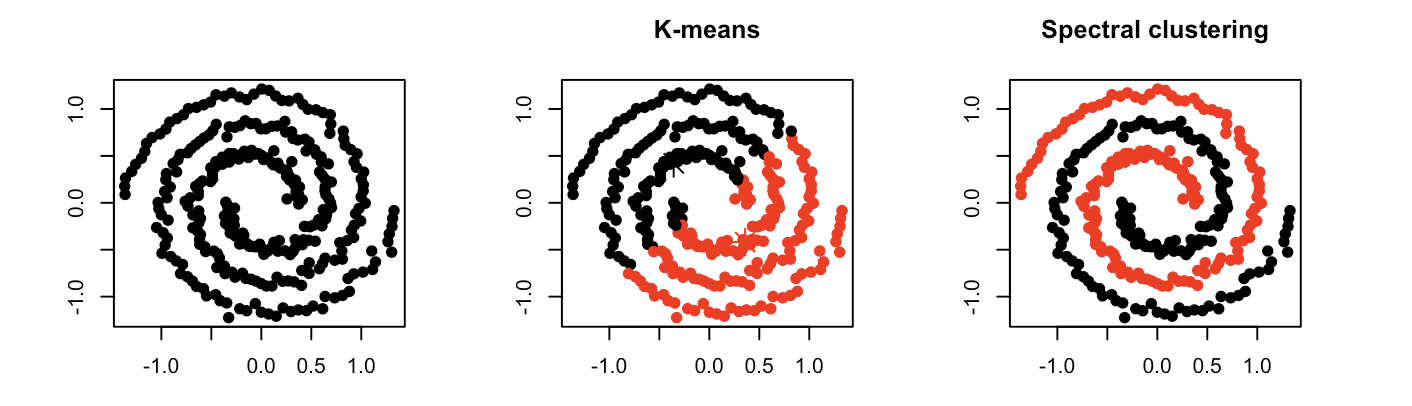
각 접근에는 장단이 있을 것이고, 당연히 군집화하고자 하는 데이터가 어떻게 생겼는지에 따라 선택이 달라져야 합니다. 예를 들어 저 맨 위 그림 같은 데이터라면, K-평균보다는 스펙트럴 클러스터링이 우리가 원하는 군집을 찾는 데 적합합니다.
어떻게 할까?
스펙트럴 클러스터링을 하는 방법은 크게 다음 두 가지 단계로 아주아주 간단하게 나눠볼 수 있습니다.
- 유사도 그래프를 만든다.
- 그래프를 쪼개서 여러 개의 클러스터를 얻는다.
유사도 그래프 만들기
우리에게 주어진 데이터 $\mathrm{x} = \left[ x_1, x_2, \cdots, x_n\right]$ 가 있을 때, 가장 먼저 해야 할 일은 이 $n$개의 데이터셋에 대해 모든 데이터포인트 간의 유사도를 표현하는 $n \times n$ 행렬을 만드는 것입니다. 다른 말로는 각 데이터를 노드로 하는 유사도 그래프를 찾아야 합니다. 이때 이 그래프는 다음과 같았으면 좋겠습니다.
- 연결된 노드 쌍마다 각자 얼마나 유사한지에 따라 엣지에 가중치가 부여된다. (Weighted)
- 그 가중치는 하나의 노드 쌍에 대해 하나의 값으로 정해져 있다. 즉 $x_j$ → $x_i$ 와 $x_i$ → $x_j$ 가 다르지 않다. (Undirected)
이 그래프를 만들 때는 $x_i$가 $x_j$에 대해 얼만큼 혹은 몇번째로 가까워야 둘이 연결되었다고 봐 줄 것인지에 따라 여러 가지 선택지가 있습니다.
- $\varepsilon$-이웃($\varepsilon$-neighbor) 그래프: 거리가 $\varepsilon$보다 가까운 노드만 연결하고 나머지는 연결하지 않는다.
- KNN(K-nearest Neighbor) 그래프: 각 노드 주변의 가장 가까운 k개의 이웃만 연결하고 나머지는 연결하지 않는다.
- 단 이 방법을 사용할 때 주의해야 할 것은 우리가 방향이 없는 그래프를 원한다는 점. A에게는 B가 nearest인데 B에게는 A가 nearest가 아닌 이슈가 있을 수 있다. 그래서 둘 다 해당일 때만 엣지를 생성하든지 둘중 하나라도 되면 방향 무시하고 생성하든지 하는 식으로 살짝 조정이 필요하다.
- 완전 연결 그래프(Fully connected) 그래프: 누락 없이 모든 노드를 연결한다.
연결되었는지 아닌지뿐만 아니라 얼마나 강하게(가까이) 연결되어 있는지도 중요합니다. 이 행렬의 원소 값은 무조건 1 또는 0이 아니라, 연결되지 않은 엣지일 경우 0, 연결된 엣지일 경우 거리가 가까울수록(=유사도가 높을수록) 큰 값을 갖도록 하는 가중치를 설정합니다. 보통 다음과 같이 가우시안 커널을 이용합니다.
\[w_{ij} = \exp(-\frac{\Vert x_i -x_j \Vert^2}{ 2 \sigma^2})\]이걸 인접(Adjacency) 행렬이라고도 합니다. 또는 유사도(Similartiy) 행렬이라고 부를 수도 있겠네요. 대칭 행렬이고요. 여기서는 $A$나 $S$ 말고 그냥 $W$라고 하겠습니다.
이 $W$는 다음과 같은 성질을 가지고 있습니다.
- $w_{ij} \ge 0$ ($x_i$ 와 $x_j$가 더 유사할수록 큰 값이 부여되는 가중치)
- $w_{ii} = 0$ ($x_i$ 와 $x_i$에 대해서는 0으로 설정)
- $w_{ij} = w_{ji}$ *무방향 그래프, 대칭 행렬
이제 우리는 원래 데이터를 클러스터로 나누는 문제에서 주어진 그래프를 작은 그래프로 나누는 문제로 바꾸었습니다. 클러스터링의 기본 목적을 기억해 봅시다.
- (원래 문제) 주어진 데이터포인트들을 클러스터로 나누되, 같은 클러스터 내에서는 데이터포인트 간 유사도가 높고 다른 클러스터 간에서는 유사도가 낮게 하자.
- (새로운 문제) 주어진 그래프의 노드들을 클러스터로 나누되, 같은 클러스터 내에서는 엣지의 가중치 합이 높고 다른 클러스터 간에는 연결하는 엣지의 가중치 합이 낮게 하자.
이제 유사도 그래프를 2개 혹은 그 이상의 그래프로 쪼개보겠습니다. 그 전에 몇 가지 처음 보는 개념이 필요합니다.
그래프 쪼개기 문제 정의 - Cut?
그래프 내부에 노드들의 집합 A, B (Subgraph)이 있을 때, A에서 B를 연결하는 엣지들의 가중치의 합을 Cut이라고 부르기로 합니다.
\[Cut(A,B) = \sum_{i \in A, j\in B} w_{ij}\]물론 하나의 집합 내부에서도 똑같이 계산할 수 있습니다. $Cut(A,A)$ 는 A 내부 엣지들의 모든 가중치의 합입니다.
만약 우리가 데이터를 2개의 군집으로 잘 나누고 싶다면, 나눠진 군집 2개가 서로 최대한 멀리 떨어져 있으면 됩니다. 즉 두 그룹을 연결하는 엣지들의 가중치 합이 적으면 된다는 뜻이고, 이 말은 $\text{cut}(A, A^c)$ 를 최소화하고 싶다는 뜻입니다. 이것이 바로 Minimum cut의 아이디어입니다.
계산은 어렵지 않으나, 종종 아래와 같은 결과가 나오곤 합니다.
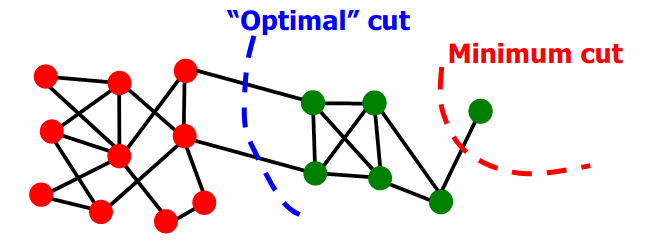Minimum cut의 잘못된 예 - 그림 출처
- 파란선: 군집을 나누는 Cut
- 빨간선: 혼자 동떨어진 노드와 나머지들을 나누는 Cut → Minimum cut이 보기엔 얘가 제일 낫다! 저 하나의 엣지만 가중치가 적으면 되니까.
근데 나는 아웃라이어를 찾고 싶은 게 아니라 클러스터를 찾고 싶은 건데? 🤔
그러면 $\text{Cut} (A, A^c)$ 는 작게 유지하되, 나눠지는 2개 군집의 크기를 비슷하게 유지하도록 조건을 추가하면 어떨까요?
여기서 RatioCut이 등장합니다.
\[RatioCut(A) = Cut(A, A^c) \cdot (\frac{1}{\vert A \vert} +\frac{1}{\vert A^c \vert})\]위 식의 뒷부분을 보면 전체 노드가 $n$개라고 할 때, $\vert A \vert$ 로 표시된 집합 $A$의 크기(cardinality)가 $\frac{n}{2}$에 가까울수록 작아진다는 게 보이실 것입니다. 즉 Cut 자체도 작아야 하지만, $A$와 $A^c$가 비슷한 크기를 가져야 이 값이 작아집니다.
이제 우리가 풀어야 하는 문제는 $\arg \min \text{RatioCut}$ 으로 정했습니다.
그래프 쪼개기 문제 풀기 - 라플라시안 행렬
슬프게도 이 문제는 NP-hard라고 합니다. (*궁금하시면 여기를 살펴보시고, 안 궁금하시다면 그냥 풀기 어렵다 정도로 생각하시고 넘어가셔도 됩니다.)
그래서 우리는 이것을 다른 문제로 바꿀 것입니다. 그러기 위해서 우선 라플라시안 행렬(Laplacian matrix)를 만들 겁니다. 만드는 방법은 다음과 같습니다.
\[L = D-W\]$W$가 어떤 행렬인지는 앞서 설명했죠. 그럼 $D$는 뭘까요? $W$로부터 만들어진 대각행렬인데, $D$의 대각 원소들은 모든 노드들에 대해 해당 노드와 연결된 엣지들의 가중치의 합을 계산한 degree입니다. 나머지 자리들은 0으로 채워줍니다.
$d_i = \sum^n_{j=1} w_{ij}$
\[D = \begin{bmatrix} d_1 & & & \\ & d_2 & & \\ & &\ddots \\ &&& d_n \end{bmatrix}\]
이제 라플라시안 행렬 $L$이 뭔지는 알았고 만들 수도 있습니다.
그 다음 과정은 아래 3가지를 순차적으로 따라가면 됩니다.
그 과정에서 제법 많은 증명이 필요합니다. 이 글에는 결론 위주로 기술할 것인데요, 제가 주로 참고한 모든 식의 증명이 정말 잘 정리된 페이지가 있습니다. 아래 부분 읽다가 이 식이 대체 왜? 라는 생각이 드신다면 한번쯤 방문해 보시길 추천해 드립니다. 그리고 고유벡터와 고유값의 개념 정도는 필요합니다. 그건 저 페이지에 가셔도 설명이 없으니 📍 여기를 한번 찍고 와주세요!
- 우리가 풀고 싶은 문제를 어떻게 $L$이 들어간 문제로 바꿀까?
그래프의 각 노드들을 실수로 바꿔주는 맵핑 $f$가 있다고 하자.
\[f = \begin{bmatrix} f (\mathbb{v_1} ) \\ f (\mathbb{v_2}) \\ \cdots \\ f (\mathbb{v_n}) \end{bmatrix} = \begin{bmatrix} f_1 \\ f_2 \\ \cdots \\ f_3 \end{bmatrix}\]각 노드에 대해
\[f_A(i) = \begin{cases} \sqrt{\frac{\vert A^c \vert}{\vert A \vert}} & \mathbb{v}_i \in A \\ - \sqrt{\frac{\vert A \vert}{\vert A^c \vert}} & \mathbb{v}_i \in A^c \end{cases}\]그리고 indicator 함수도 다음과 같이 정의한다.
\[\mathbf{1}_A(i) = \begin{cases} 1 & v_i \in A \\ 0 & v_i \in A^c\end{cases}\]- $f^TLf = \frac{1}{2} \sum_{ij} w_{ij} (f_i-f_j)^2$ 이고, $\text{RatioCut}(A) = n \cdot f_A^T L f_A$ (*증명 필요)
- 즉 $\arg \min \text{RatioCut}(A) = \arg \min \text f_A^T Lf_A$
- 이때 $f_A \cdot \mathbb{1}_V = 0$
- NP-hard이므로 $\arg \min \text f^T Lf$ 로 relax한다! 이제 $f$만 구하면 된다.
- 왜 $L$의 2번째로 작은 고유값에 대응하는 고유벡터가 그 문제의 답일까?
- Rayleigh-Ritz Theorem이라는 정리가 있다. 내용은 간단하게,
- Raleigh Quotient $R(\mathrm{x}) = \frac{\Vert A \mathrm{x} \Vert ^2}{\Vert \mathrm{x} \Vert} = \frac{\mathrm{x}^T S \mathrm{x}}{\mathrm{x}^T\mathrm{x}}$ 가 있다 ($\mathrm{x}$는 벡터, $S$는 어떤 행렬 $A$에 대해 $S=A^TA$ 대칭행렬).
- $S$의 고유값 $\lambda_1 \le \lambda_2 \le \cdots \le \lambda _n$에 과 각각 대응하는 고유벡터 $\mathrm{v_1}, \mathrm{v_2}, \cdots, \mathrm{v_n}$가 있다.
- $R(\mathrm{x})$의 최대값은 $\mathrm{x} = \mathrm{v_n}$ 일 때 $\lambda_n$이고 (가장 큰 고유값), 최소값은 $\mathrm{x} = \mathrm{v}_1$ 일 때 $\lambda_1$이고 (가장 작은 고유값)
- 참고
- 위 정리를 이용하여 $L$의 첫번째로 0이 아닌 가장 작은 고유값(Fiedler value라고도 부른다)에 해당하는 두번째 고유벡터가 우리가 찾는 답이다.
- (참고로 가장 작은 고유값은 0이고 이에 대응하는 고유벡터는 1이다.)
- Rayleigh-Ritz Theorem이라는 정리가 있다. 내용은 간단하게,
- 고유벡터 구했다. 이걸로 뭘 하라고?
- 즉 이제 해당 고유벡터를 구해서 $f$로 쓰는데,
- 애초에 $f$를 어떻게 정의했는지 생각해보면, $f_A$는 각 노드가 $A$에 속하면 $f≥0$ 이고 속하지 않으면 $f<0$이도록 맵핑했다.
- 따라서 각 데이터포인트들에 대해 $f$ 값이 음수인지 양수인지에 따라 군집을 구분할 수 있고, 보다 안전하게 $k=2$인 K-Means 알고리즘을 적용한다면 2개의 클러스터로 잘 쪼개질 것이다!
- 클러스터를 얻었다. 👏
2개 말고 k개의 군집을 찾고 싶다면 - 일반화
여러 개의 클러스터를 찾는 경우라면? 2개로 쪼갠 다음 또 각각을 2개로 나누는 식으로 bi-partitioning을 반복해도 됩니다. 하지만 비효율적이고 불안정한(정보 손실이 발생하는) 방법입니다. 처음부터 한번에 여러 개의 클러스터를 찾고 싶어요. 그러면 간단히 말하면, 고유벡터를 여러 개를 쓰면 됩니다.
상세히 처음부터 살펴보면 문제는 다시 이렇게 정의됩니다.
\[RatioCut(A_1, \cdots, A_k) = \sum^k_{i=1} \frac{Cut (A_i)}{\vert A_i \vert}\]그러니까 전체 그래프를 $A_1$부터 $A_k$로 나누고 싶은 것이죠. 과정은 비슷합니다.
- 다음과 같이 indicator 벡터를 정의한다.
- $(H^TH) = I_n$ 인 orthogonal 행렬 $H$
- 2가지를 먼저 증명
- $\frac{\text{Cut}(A)}{\vert A_l \vert} = \frac{1}{2}\sum w_{ij} (\frac{1}{\sqrt{\vert A_l \vert}})^2 +$ $\frac{1}{2}\sum w_{ij} (-\frac{1}{\sqrt{\vert A_l \vert}})^2$ = $h_l^T Lh_l$
- $(H^TLH)_{ll} = h_l^TLh_l$
- $\text{RatioCut}(A_1, \cdots, A_k) = \sum^k {l=1} h_l^TLh_l = \sum^k _{l=1} (H^TLH){ll} = \text{Tr}(H^TLH)$
- Tr: Trace!
- 즉 우리가 풀어야 하는 문제를 $\arg \min \text{Tr} (H^TLH)$ 로 바꾸었고
- 동일하게 Rayleigh-Ritz 정리를 확장하여 이 Trace 값을 최소화하는 행렬 $H$는 $L$의 가장 작은 $k$개의 고유값에 대응하는 $k$개의 벡터를 붙여 만든 행렬임을 알 수 있다.
- 나머지 단계는 2개 할 때랑 비슷하게, $h$를 각 노드가 $A_i$에 속하면 양수의 값을, 다른 노드에는 0을 맵핑하도록 정의했다는 것을 기억하자. 다른 $h$들은 이 노드에 0을 주었다.
- 즉 $k$개 차원 중 하나에서만 양수를 가지고 나머지는 다 0으로 각자 클러스터마다 맵핑이 되었을 것이고, 각 행마다 하나의 양수값만 있어야 한다.
- 그러면 $\mathbb{R}^k$ 의 새로운 데이터포인트들에서 $k$개 클러스터를 얻을 수 있고 역시 k-means를 쓰면 클러스터가 쪼개질 것이다!
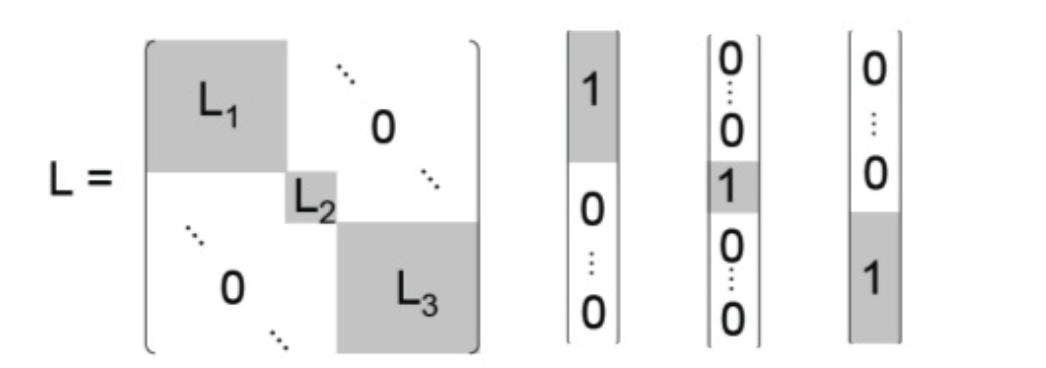$k=3$ 라면 대충 고유 벡터들이 이런 모양일 것! 그림 출처
지금까지의 과정을 조금 다르게 이해해 본다면, 우리가 가진 원래의 데이터를 새로운 더 낮은 차원의 데이터로 사영한 후 그 데이터를 가지고 클러스터링을 하는 것과 동일하다고 볼 수 있습니다. PCA를 아시는 분이라면 PCA에서 주성분 뽑아내는 것이라고 생각하면 이해가 되실 거예요.
예컨대 2개 군집으로 나누는 문제에서 우리가 최종적으로 얻은 고유벡터를 $v$ 라고 하면, 이는 원래의 데이터 $x$ 에 대응하는 새로운 데이터포인트들로 보면 됩니다. 즉 $x_1$ 이 $v_1$ 이고, $x_n$ 이 $v_n$ (각 데이터포인트)인 것이죠.
\[v = \begin{pmatrix} v_1 \\ v_2 \\ \cdots \\ v_n \end{pmatrix}\]고유벡터를 k개 골랐다면? 원래 $n \times n$이었던 데이터는 $n \times k$ 개로 차원이 감소하게 됩니다. 즉 아래 행렬에서 각 행이 새로운 $x_1$, $x_2$, $x_3$, $\cdots$ 인 것입니다(고유값이 작은 순서대로).
\[V = [\mathbf{v_1}, \mathbf{v_2}, \cdots, \mathbf{v_k}] = \begin{bmatrix} v_{11} & v_{12} & \cdots & v_{1k} \\ v_{21} & v_{22} & \cdots & v_{2k} \\ \cdots \\ v_{n1} & v_{n2} & \cdots & v_{nk} \end{bmatrix}\]이제 이 새로운 데이터포인트들을 k-means 알고리즘을 사용하여 K개의 클러스터로 분할하는 것입니다.
주요 내용은 아니지만 더 궁금했던 것들
1. $k$를 선택하는 방법
이 페이퍼에서는 Eigengap을 통해 k를 선택하는 방법을 설명해주고 있습니다.
- Eigengap : $\vert \lambda_n - \lambda_{n+1} \vert$ (크기순으로 늘어놓았을 때 $n$번째 고유값과 $n+1$ 번째 고유값의 차이)
- 쉽게 말하면 $n$까지 고유값이 비슷하게 작다가 $n+1$에서 갑자기 커지는 계단 모양이 몇 번 나타나느냐? 를 찾자는 것.
- 데이터가 확실히 분리되어 있을수록(클러스터가 뚜렷할수록) 고유값이 갑자기 커지는 걸 볼 수 있다.
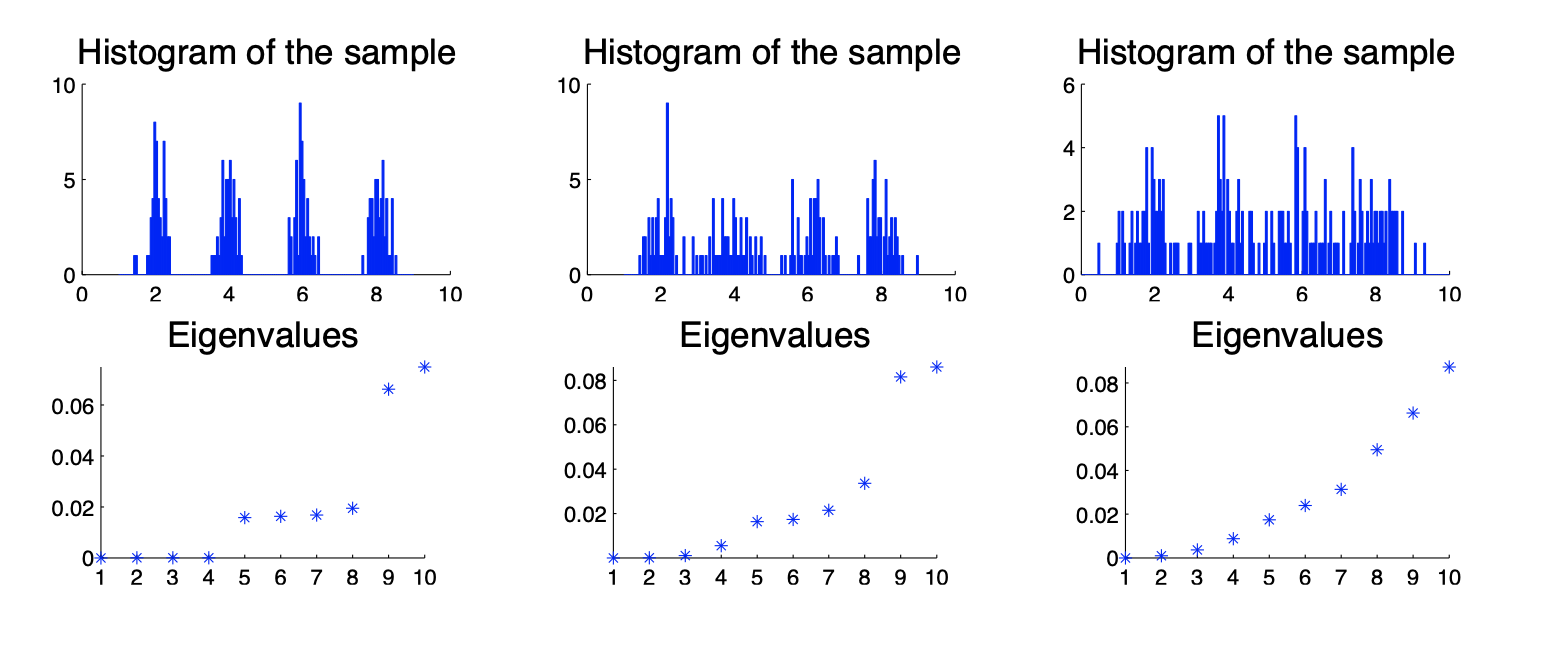
2. Unnormalized Cut? Normalized Cut?
위에서 다룬 RatioCut은 사실 Unnormalized Cut입니다.
Normalized Cut은 최소화하고자 하는 컷을 어떻게 정의하느냐가 다릅니다.
\[NormalizedCut(A) = Cut(A, A^c) \cdot (\frac{1}{Vol (A)} +\frac{1}{Vol (A^c)})\]$\text{Vol}(A)$ 는 $A$에 속한 모든 노드에 연결된 모든 가중치의 합으로 정의합니다. 즉, $\text{Cut}(A,A)$ 에 $\text{Cut}(A,B)$를 더해준 값입니다.
이게 RatioCut에 비해 어떤 장점을 지닐까요? $\text{Vol}(A)$와 $\text{Vol}(A^c)$가 비슷하고, 동시에 각 군집 내부 볼륨이 커질수록 NormalizedCut은 작아집니다. 군집 내부 볼륨이 크다는 것은 군집 내부 노드들이 서로 유사도가 크다는 뜻입니다.
다시 클러스터링의 기본 목적을 생각해 봅시다.
- 군집 간 유사도를 최소화하는 것 (between-cluster similarity) → $\text{Cut}(A, A^c)$ 을 줄인다.
- 군집 내 유사도를 최대화하는 것 (within-cluster similarity) → $\text{Cut}(A, A)$ 와 $\text{Cut}(A^c, A^c)$ ( *$A$와 $A^c$ 각각의 내부 유사도)를 늘린다.
즉 RatioCut의 경우는 군집 간 유사도 최소화라는 목적은 충족하지만 군집 내 유사도 최대화는 충족하지 못합니다. 반면 NormalizedCut은 두 개 목적 모두를 충족하도록 설정된 문제입니다. 풀어서 써보면,
$\text{Cut}(A,A) = \text{Vol}(A) - \text{Cut}(A,A^c)$
이걸 최대화하려면 $\text{Vol}(A)$는 크고 $\text{Cut}(A, A^c)$는 작아야 합니다. NormalizedCut 식과 똑같죠.
RatioCut 같은 경우에는 라플라시안 행렬을 $L = D - W$로 썼었습니다. NormalizedCut은 다음 2개 중 하나를 씁니다. 다른 부분들(이 라플라시안 행렬의 $k$개 고유벡터를 선택하는 부분)은 비슷합니다.
- $L_{sym} = D^{-\frac{1}{2}}LD^{-\frac{1}{2}} = I - D^{-\frac{1}{2}}WD^{-\frac{1}{2}}$
- $L_{rw} = D^{-1}L = I-D^{-1}W$
그래프가 normal하고, 대부분의 노드가 대략 같은 degree를 가지는 경우 $L, L_{sym}, L_{rw}$ 세 개의 방법이 거의 동일한 클러스터링 결과를 도출하지만, degree가 넓게 퍼진 분포일 경우 normalized된 방법이 낫고, $L_{rw}$ 가 더 좋다고 하네요.