수학을 까먹은 사람을 위한 특이값분해(SVD)

특이값분해(SVD)에 대해 대부분의 선수지식을 포함하여 이해하기 쉽게 설명한 글입니다. SVD의 증명, 기하학적 의미, python으로 이미지 압축하는 예시를 포함하고 있습니다. 제가 이전에 작성한 고유값분해에 대한 글을 읽고 오시거나 어떤 통로로든 고유값분해가 무엇인지를 알고 오시면 좋습니다.

SVD 식 만들어보기

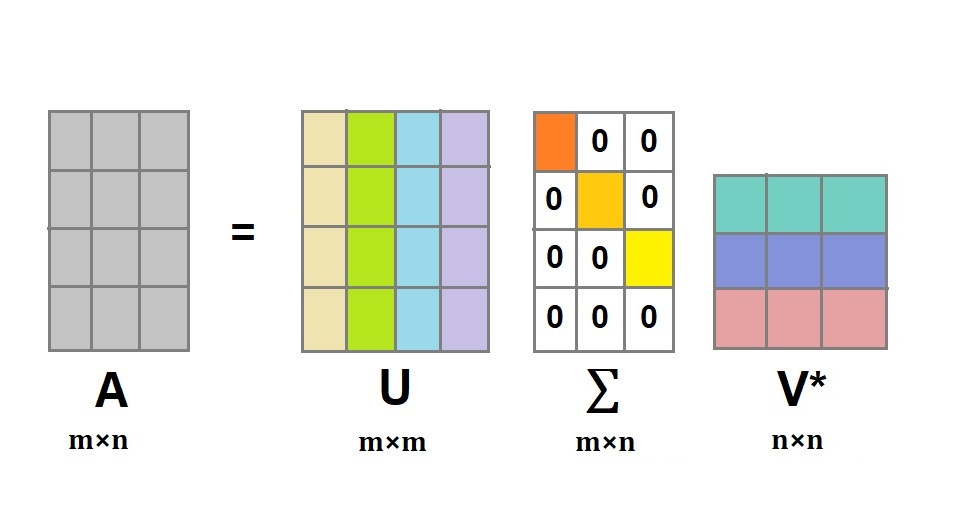
일단 정의부터 써봅시다. 실수값으로 이루어진 모든 $m \times n$ 행렬 $A$ 는 다음과 같이 특이값분해될 수 있습니다.

잠깐 이 문장으로 알 수 있는 사실은, 그 정의상 정방행렬($m = n$ )에서만 가능하고 또 특정 조건(서로 독립인 $n$개의 고유벡터가 존재)을 만족해야만 가능했던 고유값분해와 달리 특이값분해는 꼭 필요한 조건이 없다는 것입니다.

\[A = U\Sigma V^T\]

그림 출처

• $U$는 $m \times m$ 직교행렬이며 $AA^T$를 고유값분해해서 얻은 고유벡터를 열로 하여 만들어졌다.
• $V$는 $n \times n$ 직교행렬이며 $A^TA$를 고유값분해해서 얻은 고유벡터를 열로 하여 만들어졌다.
• $\Sigma$는 $m \times n$ 대각행렬이며 $AA^T$, $A^TA$를 고유값분해해서 얻은 고유값들의 제곱근을 취한 값을 좌상단부터 대각 원소로 가지고, 나머지 부분들은 다 0으로 만들어졌다.

정의부터 던지면 이게 다 뭔 소리지 라는 생각이 듭니다. 이 세 가지 행렬이 왜 나오는지 천천히 뜯어보고 증명도 해볼 것입니다.

일단 모든 행렬에 대해 그 행렬과 전치행렬을 곱한 행렬인 $AA^T$, $A^TA$ 이 두 가지 행렬은 좀 특별한 구석이 있는데요, 이 행렬의 특징들에 대해 알 필요가 있습니다. 그게 왜 그런데? 라는 생각이 드시는 분들을 위해 ‘왜’도 다 적어놨지만, 사실 그냥 그렇구나 하고 넘어가셔도 무방합니다.

• 정방행렬이다.
  • $AA^T$: $m \times n$ 행렬과 $n \times m$ 행렬을 곱했으니까 $m \times m$ 행렬임
  • $A^TA$: $n \times m$ 행렬과 $m \times n$ 행렬을 곱했으니까 $n \times n$ 행렬임
• 대칭행렬이다.
  • 💡 대칭행렬이 뭐더라? 시각적으로는 대각 기준으로 반 접으면 접히는 값들이 같다는 것이며 정확한 정의로는 전치해도 원래 행렬과 동일하다는 것이다. 즉 $X = X^T$
  • 전치해보면 아주 쉽다. $(AA^T)^T = AA^T$, $(A^TA)^T = A^TA$
• 고유값분해될 수 있다(=실수 고유값을 가짐). 왜냐면 모든 대칭행렬은 고유값분해될 수 있기 때문에.
  • 💡 다시 강조하면 모든 실수 행렬이 고유값분해 될 수 있는 것은 아니며 어떤 행렬은 고유값으로 허수값을 가질 수도 있다! 하지만 대칭행렬은 고유값의 실수임이 보장된다는 건데,
  • 실수 대칭행렬 $S$의 고유값 $\lambda$ 이 있을 때 (즉 $S \mathbf{v} = \lambda \mathbf{v}$) … 1️⃣
  • 켤레값을 취하면 $\bar{S} \bar{\mathbf{v}} = \bar{\lambda} \bar{\mathbf{v}}$ 이며 $S$는 실수행렬이므로 ($\bar{S} = S$) $S \bar{\mathbf{v}} = \bar{\lambda} \bar{\mathbf{v}}$
  • 전치하면 $\bar{\mathbf{v}}^TS^T = \bar{\lambda} \bar{\mathbf{v}}^T$ 이며 $S$는 대칭이므로 ($S=S^T$) $\bar{\mathbf{v}}^TS = \bar{\lambda} \bar{\mathbf{v}}^T$ … 2️⃣
  • 1️⃣ $S \mathbf{v} = \lambda \mathbf{v}$ 에 $\bar{\mathbf{v}}^T$를 곱하면, $\bar{\mathbf{v}}^T S \mathbf{v} = \lambda \bar{\mathbf{v}}^T \mathbf{v}$
  • 2️⃣ $\bar{\mathbf{v}}^TS = \bar{\lambda} \bar{\mathbf{v}}^T$ 에 $\mathbf{v}$를 곱하면, $\bar{\mathbf{v}}^TS \mathbf{v} = \bar{\lambda} \bar{\mathbf{v}}^T \mathbf{v}$
  • 위 두 식의 좌변이 같으므로 우변도 같아야 함. $\lambda = \bar{\lambda}$ 가 되어 $\lambda$ 는 실수임.
• 고유벡터들이 직교한다. 왜냐면 대칭행렬의 고유벡터들은 항상 직교하기 때문에.
  • 대칭행렬 $S$의 서로 다른 고유벡터 $\mathbf{v}_1, \mathbf{v}_2$와 그에 대응하는 고유값 $\lambda_1$, $\lambda_2$가 있을 때 (즉 $S\mathbf{v}_1 = \lambda_1 \mathbf{v}_1$, $S\mathbf{v}_2 = \lambda_2 \mathbf{v}_2$)
  • $\lambda_1 \mathbf{v}^T_1 \mathbf{v}_2 = (S\mathbf{v}_1)^T \mathbf{v}_2 = \mathbf{v}_1^TS^T\mathbf{v}_2 = \mathbf{v}_1^TS\mathbf{v}_2 = \mathbf{v}^T_1\lambda_2\mathbf{v}_2 = \lambda_2\mathbf{v}^T_1 \mathbf{v}_2$
  • $\lambda_1\mathbf{v}^T_1\mathbf{v}_2 - \lambda_2 \mathbf{v}^T_1 \mathbf{v}_2 = (\lambda_1 - \lambda_2) \mathbf{v}^T_1 \mathbf{v}_2 = 0$
  • 💡 직교가 뭐더라? 두 벡터의 내적이 0인 것이다. 즉 $\mathbf{v}_1^T\mathbf{v}_2=0$ 이면 두 벡터는 직교한다.
  • 여기서 서로 다른 두 고유값은 같은 값일 수 없으므로 ($\lambda_1 - \lambda_2 \neq 0$ ) $\mathbf{v}_1^T\mathbf{v}_2=0$
• 고유값들이 모두 0 이상의 값을 가진다. 왜냐면 semi-positive definite한 행렬이기 때문에.
  • 💡 positive definite가 뭐더라? 영벡터가 아닌 모든 벡터 $\mathbf{v}$에 대해 항상 $\mathbf{v}^TA\mathbf{v} >0$ 일 때 $A$를 positive definite하다고 하고, $\ge 0$일 때 semi-positive definite 하다고 함. 행렬에도 부호가 있다고 이해하면 편하다!
    • 어떤 semi-positive definite 행렬과 그 고유값에 대해, $A\mathbf{v} = \lambda \mathbf{v}$ 의 양변에 $\mathbf{v}^T$를 곱하면, $\mathbf{v}^TA\mathbf{v} = \lambda \mathbf{v}\mathbf{v}^T \ge 0$ 결국 고유값과 벡터의 내적값을 곱한 게 0 이상이어야 하므로 고유값도 0 이상이어야 한다는 결론.
  • $A^TA$ 에 대해 $\mathbf{v}^TA^TA\mathbf{v}$ 이렇게 곱해보면 결국 $(A\mathbf{v})^T(A\mathbf{v}) = \Vert A\mathbf{v} \Vert ^2 \ge 0$ 이므로 semi-positive definite이고, 그래서 고유값들이 0 이상임.

위 사실들을 생각하면서 특이값분해를 증명해봅시다.

우선 $A^TA$ 부터 보겠습니다. 이 행렬은 고유값분해될 수 있기 때문에, 여러 개의 고유값과 그에 상응하는 고유벡터가 존재할 것입니다. 다음과 같은 고유값 $\lambda_i$와 고유벡터 $\mathbf{v}_i$ 가 있다는 것이죠.

\(A^TA\mathbf{v}_i = \lambda_i\mathbf{v}_i = \sigma_i^2\mathbf{v}_i\) 이때 $A^TA$ 의 모든 고유값은 0 이상의 값을 가진다는 것을 기억하면, $\lambda_i$는 제곱근을 가질 것이고 그걸 $\sigma_i$라고 써줬습니다.

이제 $\mathbf{v}_i$ 의 특징을 생각해봅시다. 고유값분해에 대해 떠올려보면, 고유값에 대응하는 고유벡터는 굉장히 많은 수로 존재할 수 있습니다. 제가 이전 글에 썼던 예시를 그대로 가져와보면,

\[\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = 3 \begin{bmatrix} 1 \\ 1 \end{bmatrix}\]

이 행렬의 고유값 3에 대해 고유벡터는 (1,1)이 될 수도 있고 (50000, 50000)이 될 수도 있고 (-1234, -1234)가 될 수도 있다고 했었죠. 방향만 같으면 크기는 마음대로 할 수 있다는 겁니다. 따라서 우리는 보통 노름(어떤 벡터를 자기자신과 내적한 값, 즉 $\mathbf{v}^T\mathbf{v}$ 의 양의 제곱근)이 1이 되는 벡터로 고유벡터를 고릅니다. 이런 벡터를 단위벡터라고 합니다. 어떤 벡터든 노름값으로 나눠서 크기를 조정해주면 단위벡터로 만들어줄 수 있습니다. 따라서 $\mathbf{v}_i ^T \mathbf{v}_i =1$ 입니다.

또 앞서 언급했듯 $A^TA$는 대칭행렬이라서 모든 고유벡터가 서로 직교합니다. 따라서 서로다른 $i$,$j$ 에 대해 $\mathbf{v}_i ^T \mathbf{v}_j =0$이라는 사실도 기억합시다. 따라서 모든 $\mathbf{v}$를 열로 이어붙여 행렬을 만든다면 이 행렬은 직교행렬이겠죠.

여기까지 보면, 다음 문장은 더 이상 설명할 게 없을 겁니다.

• $V$는 $n \times n$ 직교행렬이며 $A^TA$를 고유값분해해서 얻은 고유벡터를 열로 하여 만들어졌다.

추가로, $A^TA\mathbf{v}_i = \sigma_i^2\mathbf{v}_i$ 이 식의 양변에 $\mathbf{v}_i^T$ 를 곱해 봅시다.

\[\mathbf{v}_i^TA^TA\mathbf{v}_i = \sigma_i^2\mathbf{v}_i^T\mathbf{v}_i\]

단위벡터라서 $\mathbf{v}_i ^T \mathbf{v}_i =1$ 이므로, \((A\mathbf{v}_i)^TA\mathbf{v}_i = \sigma_i^2\)

$A\mathbf{v}_i$ 의 노름이 $\sigma_i$란 사실을 알 수 있습니다. 이 말은 다름 아니라, $\frac{A\mathbf{v}_i}{\sigma_i}$ 는 또다른 단위벡터라는 뜻이죠.

즉 모든 $A^TA$의 고유벡터 $\mathbf{v}_i$ 에 대해 다음과 같은 단위벡터 $\mathbf{u}_i$가 존재합니다.

\[\mathbf{u}_i = \frac{A\mathbf{v}_i}{\sigma_i}\]

이번엔 $A^TA\mathbf{v}_i = \sigma_i^2\mathbf{v}_i$ 이 식의 양변에 $A$ 를 곱해 봅시다.

\[AA^TA\mathbf{v}_i = \sigma_i^2A\mathbf{v}_i\]

양변을 $\sigma_i$로 나눠준다면, 최종적으로 다음과 같은 식이 도출되어 $\mathbf{u}_i$가 $AA^T$의 고유벡터이며, 그 고유값은 $\sigma_i^2$ 로, $A^TA$의 고유값과 동일하다는 사실을 알 수 있습니다.

\(AA^T (\frac{A\mathbf{v}_i}{\sigma_i}) = AA^T\mathbf{u}_i = \sigma_i^2\mathbf{u}_i\) 그 외의 다른 성질, 예를 들면 서로다른 $i$, $j$ 에 대해 $\mathbf{u}_i$, $\mathbf{u}_j$ 가 직교라는 점은 $AA^T$의 고유벡터나 $A^TA$의 고유벡터나 동일하기 때문에 다시 쓸 필요는 없겠습니다.

이제 다음 문장까지 정리가 되었습니다.

• $U$는 $m \times m$ 직교행렬이며 $AA^T$를 고유값분해해서 얻은 고유벡터를 열로 하여 만들어졌다.

다시 $A$와 $\mathbf{u}_i$ 와 $\mathbf{v}_i$의 관계식으로 돌아가면 다음과 같습니다.

\[\sigma_i\mathbf{u}_i = A\mathbf{v}_i\]

이를 개별 벡터가 아닌 행렬의 모양으로 다시 쓰면 이렇습니다.

\[U \Sigma = AV\]

여기서 이게 행렬로 쓰면 왜 이렇게 되지? $\Sigma$ 는 어떻게 생긴 행렬이지? 라는 생각이 들 수 있습니다. 그 이야기를 잠깐 해보겠습니다.

$AA^T$ 와 $A^TA$는 각각 $m$개, $n$개의 선형독립인 고유벡터를 가지고 그에 대응하는 고유값을 가질 것입니다. 그 중 일부는 0이고 일부는 0이 아닐 수 있는데요. 0이 아닌 고유값에 대해서 $AA^T$ 와 $A^TA$의 고유값이 일치한다는 사실은 위에서 보았습니다. 0이 아닌 고유값이 $r$ 개 있다고 합시다.

\[\lambda_1, \cdots, \lambda_r = \sigma^2_1,\cdots, \sigma^2_r\]

이때 $r$ 은 사실 각 행렬의 rank 값과 동일하며, 원 행렬 $A$의 rank 값과도 동일합니다. 왜인지를 생각해보면, 행렬 $S$가 고유값분해로 대각화될 수 있을 때 ($S=V \Lambda V^{-1}$) 역행렬이 있는 행렬의 곱은 rank를 변화시키지 않으므로 결국 이 행렬 $S$ 는 고유값으로 이루어진 대각행렬 $\Lambda$과 rank가 동일한 건데, 대각행렬에서 서로 독립인 열의 개수는 단순히 0이 아닌 대각원소의 개수를 센 값이기 때문입니다.

어쨌든 이 0이 아닌 고유값들의 제곱근($\sigma$)을 큰 순서대로 대각 원소로 하고, 나머지 부분은 0으로 채운 행렬을 생각해봅시다.

\[\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_r > 0\]

이 행렬은 $r \times r$이므로 $m \times n$ 으로 만들어주기 위해 ($m-r$) 행만큼, ($n-r$) 열만큼 또 0으로 채워줍니다. $m = 4$, $n = 5$, $r=3$ 인 $\Sigma$의 예시는 다음과 같습니다.

\[\begin{bmatrix} 3 & 0 & 0 &0 &0 \\ 0 & \sqrt{5} & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}\]

즉 원래 행렬 $A$는 rank-3 행렬이며, $AA^T$, $A^TA$의 0이 아닌 고유값의 제곱근은 큰 순서대로 3, $\sqrt{5}$, 2입니다. 이 값들을 행렬 $A$의 특이값(singular value) 이라고 부릅니다.

다시 $AA^T$의 고유벡터 $m$개를 열로 이어붙인 행렬을 다음과 같이 만들 수 있습니다. 다시 $m=4$의 예시입니다.

\[U = \begin{bmatrix} \mid & \mid & \mid & \mid \\ \mathbf{u_1} & \mathbf{u_2} & \mathbf{u_3} & \mathbf{u_4} \\ \mid & \mid & \mid & \mid \end{bmatrix} = \begin{bmatrix} 0 & -1 & 0 & 0 \\ -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 0 & 0 & -1 & 0 \end{bmatrix}\]

이제 행렬곱 $U\Sigma$ 를 해보면, $i=1, \cdots, m (m=4)$ 에 대해 우리가 증명했던 벡터 기준의 식의 좌변인 $\sigma_i\mathbf{u}_i$ 가 나온다는 것을 알 수 있죠. 특이한 점은 $\Sigma$에서 $r+1$부터는 다 0으로 채워줬기 때문에 $\mathbf{u}_4$ 는 곱하면 0이 되어 사실 결과에 전혀 영향을 주지 못합니다.

마찬가지로 $A^TA$의 고유벡터 $n$개를 열로 이어붙인 행렬도 만들 수 있습니다.

\[V = \begin{bmatrix} \mid & \mid & \mid & \mid& \mid \\ \mathbf{v_1} & \mathbf{v_2} & \mathbf{v_3} & \mathbf{v_4} & \mathbf{v_5} \\ \mid& \mid & \mid & \mid & \mid \end{bmatrix} = \begin{bmatrix} 0 & 0 & -1 & 0 & 0 \\ -\sqrt{0.2} & 0 & 0 & 0 & -\sqrt{0.8} \\ 0 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ -\sqrt{0.8} & 0 & 0 & 0 & \sqrt{0.2} \end{bmatrix}\]

행렬곱 $AV$는 우변이었던 $A\mathbf{v}_i$를 그대로 행렬로 쓴 것과 동일합니다.

이때 $V$는 서로 직교하는 단위벡터로 이루어진 직교행렬이기 때문에 $VV^T = I$, $V^{-1} = V^T$ 이구요. 양변에 이 행렬을 곱해주면, 이렇게 해서 드디어 출발점이었던 다음 식에 도달했습니다!

\(A = U\Sigma V^T\)

SVD의 기하학적 의미

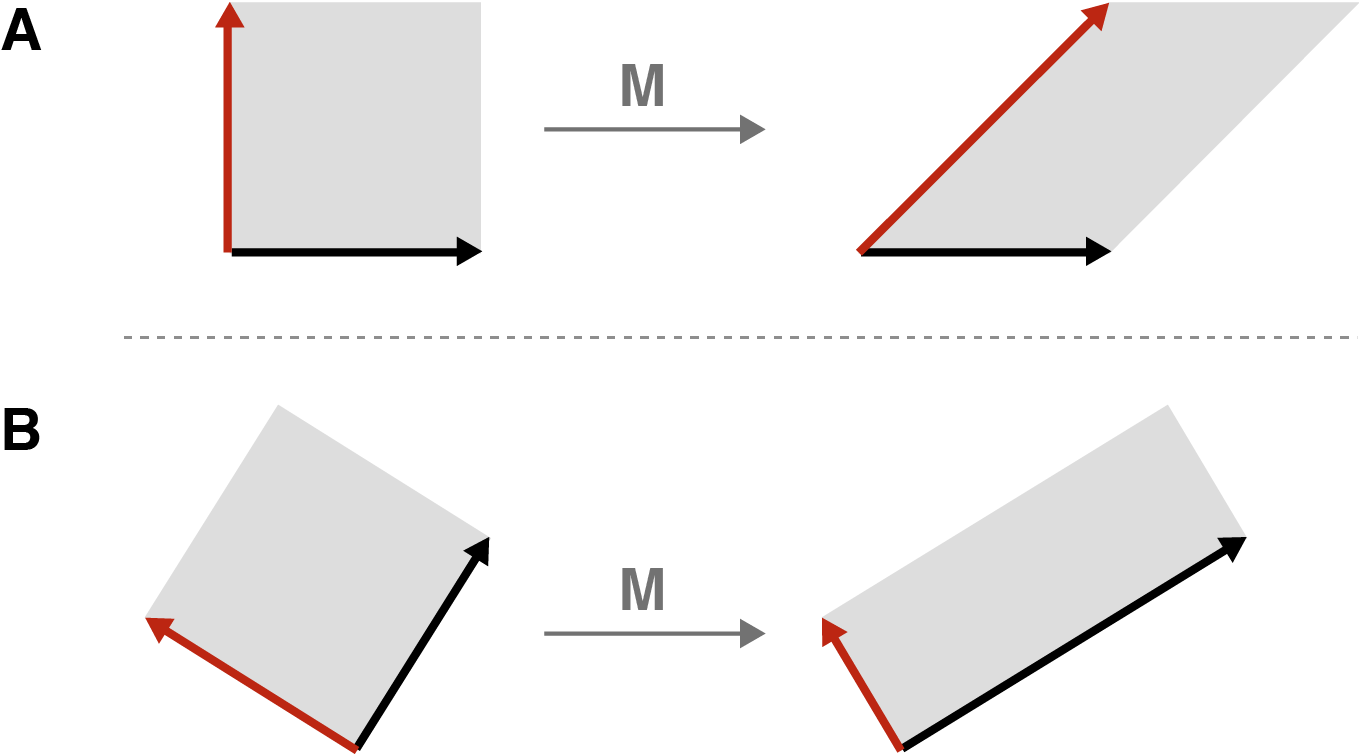
고유값분해의 기하학적 의미는 어떤 벡터에 어떤 행렬을 곱했을 때, 벡터의 크기만 변하고 방향은 변하지 않는다는 것이었습니다. 이번에는 서로 직교하는 벡터에 어떤 행렬을 곱하는 것을 상상해봅시다.

그림 출처

• A의 경우, 직교하는 두 벡터에 $M$ 이라는 행렬을 곱했을 때 사이각이 변함
• B의 경우, 직교하는 두 벡터에 $M$ 이라는 행렬을 곱했더니 여전히 직교 상태를 유지하고 있음 (다만 둘이 같이 회전했고, 각 크기는 변했음)

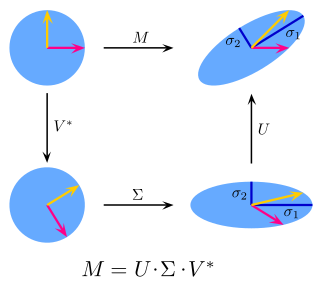
특이값 분해의 의미는 위의 B 케이스처럼 직교하는 어떤 벡터에 어떤 행렬을 곱했을 때, 크기가 변하고 회전되더라도 직교하는 상태는 변하지 않는다는 것입니다. 위에서 보인 식으로 돌아가면, $U \Sigma = AV$ 이 식에서 $A$ 는 곱해지는 행렬(선형변환)이고, $\Sigma$는 크기가 변하는(스케일링되는) 값을 의미합니다. $V$와 $U$는 반복해서 언급했듯 직교행렬이고요.

그림 출처

이를 염두에 두고 다시 $A = U\Sigma V^T$ (그림 속 $M$ )를 보면, 모든 $A$라는 행렬을 곱하는 행위는 결국 $m$차원에서 $n$차원으로 선형 변환을 하는 것을 의미하는데, 직교행렬 $U, V$는 은 곱해질 때 회전만 시킬 뿐 각도나 크기를 변화시키지 않고 $\Sigma$는 크기만 바꾸므로, 순서대로 1) $V^T$를 곱해서 회전 2) $\Sigma$를 곱해서 크기 변화 3) $U$를 곱해서 회전을 하는 것과 동일합니다. 따라서 원래 벡터의 모양을 바꾸는 것은 오로지 특이값의 크기($\Sigma$의 값)에만 달려 있습니다.

SVD의 응용

특이값분해는 데이터를 효과적으로 압축하는 데 사용될 수 있습니다. 우리가 지금까지 알아낸 SVD, 즉 다음과 같이 행렬을 분해하는 것을 Full SVD라고 합니다.

\[A = U\Sigma V^T\]

아까 $\Sigma$ 가 어떻게 생겼는지 되살려보면,

\[\begin{bmatrix} 3 & 0 & 0 &0 &0 \\ 0 & \sqrt{5} & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}\]

이런 식으로 내림차순으로 정렬된 $A$의 rank 만큼의 0이 아닌 특이값이 존재($r$개)하고, 나머지는 다 0입니다. 0인 부분은 다 날려 버리고, 이에 대응하는 $U$와 $V$의 벡터들도 $r$개만 선택하면 어떨까요? 아까 잠깐 설명했듯 $r+1$ 이후 부분부터는 결과물에 아무 영향도 주지 않기 때문에 $U_r\Sigma_r V_r^T$ 로도 원래 행렬 $A$를 얻을 수 있습니다.

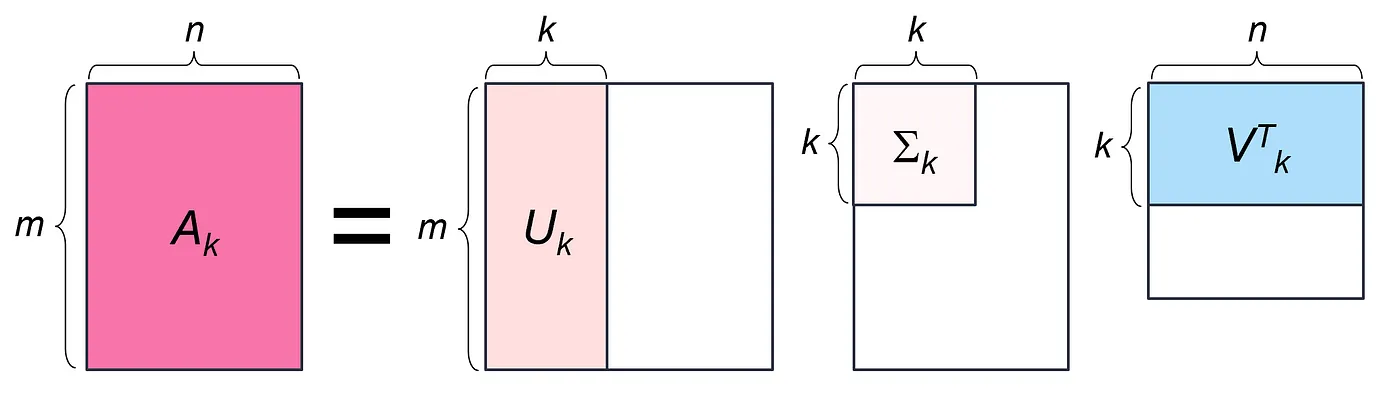
이번에는 조금 더 과감하게, 0이 아닌 특이값 중 가장 큰 $k$개만 ($k < r$) 남기고 $U$와 $V^T$도 $k$개의 열, 행만 남겨 봅시다.

그림 출처

이렇게 얻은 $A_k = U_k\Sigma_k V_k^T$ 는 원래의 $A$ 와 완전히 같지는 않은 근사행렬입니다. 전체 특이값을 다 쓰지 않았기 때문이죠. 다만 특이값 중 큰 순서대로 골랐기 때문에 노이즈를 줄이고 데이터에서 의미 있는 부분을 남기는 효과가 있습니다. $k$를 적게 잡을수록 더 많이 압축되고, 처리 비용을 줄일 수 있지만 원래 행렬인 $A$와 멀어지는 것을 감수해야겠죠. 이것을 Truncated SVD 라고 부릅니다.

이미지 압축 예시

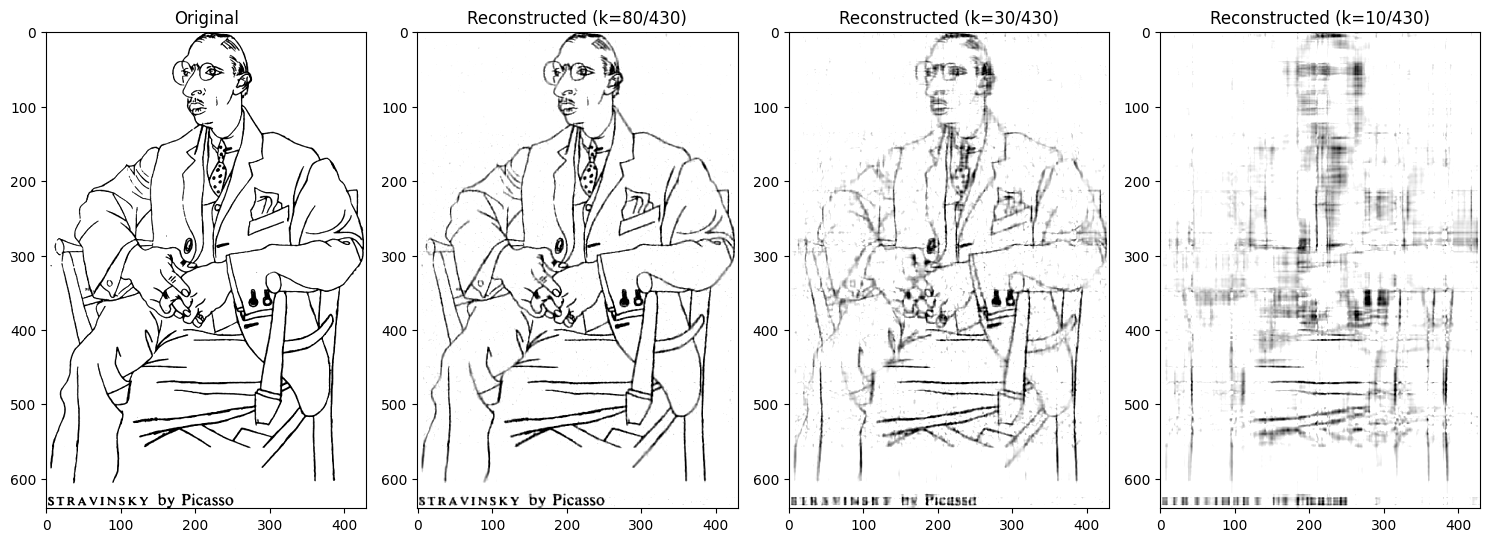
이러한 SVD는 이미지를 압축할 때 사용될 수 있습니다. 예시로 다음과 같은 그림을 압축해보겠습니다. 출처는 개발자를 위한 실전 선형대수학의 14장의 연습 문제입니다.

피카소가 그린 작곡가 스트라빈스키의 초상화

import numpy as np
import matplotlib.pyplot as plt
from skimage import io

#위 그림 불러오기
url = 'https://berggasse19.org/wp-content/uploads/2015/05/stravinsky_picasso_wikipedia.png'
strav = io.imread(url) / 255
np.shape(strauv)
# (640, 430)

우리가 압축하려는 행렬은 640 $\times$ 430 짜리입니다. SVD를 해보고, 그 다음 얻은 특이값들을 scree plot으로 시각화해 봅시다.

U,s,Vt = np.linalg.svd(strav) #python으로 SVD 수행은 이렇게나 간단하다
S = np.zeros_like(strav)
np.fill_diagonal(S,s) #특이값 행렬 만들어주기

plt.figure(figsize=(12,4))
plt.plot(s[:30],'ks-',markersize=10) #가장 큰 특이값 30개 가져오기
plt.xlabel('Component index')
plt.ylabel('Singular value')
plt.title('Scree plot of Stravinsky picture')
plt.grid()
plt.show()

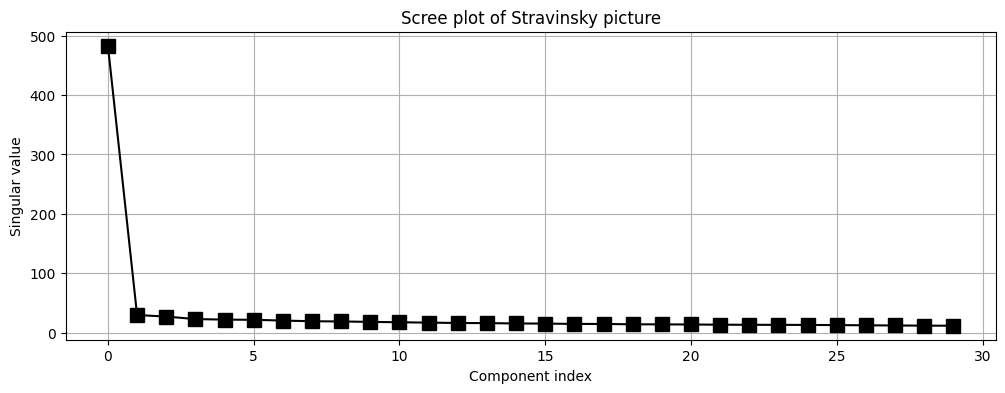총 430개의 특이값 중 30개만 표현해봤습니다. x축이 특이값 1번부터 30번을 나타내는 인덱스이며 y축은 그 값입니다. 가장 큰 특이값은 약 483이며, 그 다음 값부터는 차이가 상당히 많이 나네요.

이제 여러 개의 $k$ 값을 골라서 이미지를 압축해봅시다. $k$를 고르고, 그에 맞춰서 $U$, $S$, $V$를 자르고, 다시 곱해주면 됩니다.

#테스트해볼 k값
k_1 = 10
k_2 = 30
k_3 = 80

#reconstruction
stravRec_1 = U[:,:k_1] @ S[:k_1,:k_1] @ Vt[:k_1,:]
stravRec_2 = U[:,:k_2] @ S[:k_2,:k_2] @ Vt[:k_2,:]
stravRec_3 = U[:,:k_3] @ S[:k_3,:k_3] @ Vt[:k_3,:]

#압축된 이미지 그리기
_,axs = plt.subplots(1,4,figsize=(15,6))
axs[0].imshow(strav,cmap='gray',vmin=.1,vmax=.9)
axs[0].set_title('Original')

axs[1].imshow(stravRec_3,cmap='gray',vmin=.1,vmax=.9)
axs[1].set_title(f'Reconstructed (k={k_3}/{len(s)})') 

axs[2].imshow(stravRec_2,cmap='gray',vmin=.1,vmax=.9)
axs[2].set_title(f'Reconstructed (k={k_2}/{len(s)})')

axs[3].imshow(stravRec_1,cmap='gray',vmin=.1,vmax=.9)
axs[3].set_title(f'Reconstructed (k={k_1}/{len(s)})')

plt.tight_layout()
plt.show()

좌측에서 순서대로 원본 이미지, $k=80$, $k=30$, $k=10$입니다. 오른쪽으로 갈수록 더 적은 수의 데이터를 사용하면서 이미지로 표현한 결과물이 (원본과 대조했을 때) 알아보기 어려워진 것을 확인할 수 있죠. 첫번째 압축 이미지를 보면 430개 중 80개만 사용해도 그럭저럭 원본 이미지와 유사한 결과를 내고 있습니다.

stravSize = strav.nbytes / 1024**2 
stravRSize = stravRec_3.nbytes / 1024**2 
uSize = U[:,:k].nbytes / 1024**2 
sSize = s[:k].nbytes / 1024**2 
vSize = Vt[:k,:].nbytes / 1024**2 
print(f' Original is {stravSize:.2f} mb') 
print(f'Reconstruction is {stravRSize:.2f} mb') 
print(f'Recon vectors are {uSize+sSize+vSize:.2f} mb (using k={k} comps.)') 
print(f'\nCompression of {100*(uSize+sSize+vSize)/stravSize:.2f}%')

위와 같이 바이트 수의 백분율을 통해 압축률을 계산해보면 약 31%가 나옵니다.

참고한 글들

• Singular value decomposition
• [선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용
• 특이값 분해(SVD)의 증명
• Singular Value Decomposition (SVD), Demystified