LDA (잠재 디리클레 할당) 이해하기

토픽 모델링 기법인 LDA의 가정과 추론 방식을 쉽게 설명한 글입니다.

오늘은 잘 알려진 토픽 모델링 기법인 LDA에 대해서 알아보겠습니다. LDA는 Latent Dirichlet Allocation, 즉 잠재 디리클레 할당이라는 이름이며, 보다시피 이 이름은 3개의 단어로 이루어져 있습니다. 이 세 단어를 하나씩 뜯어보면 LDA를 이해할 수 있습니다.

잠재

잠재란 드러나지 않는다는 뜻입니다. LDA는 우리가 보고 있는 데이터인 문서가 숨겨져서 드러나지 않는 어떤 과정의 결과물이라고 가정합니다.

예를 들어,

널 초코칩으로 스프링클로 입맛 버리게 만들고 싶어, 숨기고 있지만 널 더 보고 싶어

누군가가 이런 문서를 썼다고 합시다. (출처)

이 문서가 만들어진 잠재적인(눈에 보이지 않는) 과정은 뭘까? 라는 질문에서 출발합시다. 이 말을 조금 더 쉽게 바꾸면, 이 문서를 쓴 사람은 어떤 과정을 거쳐서 이런 단어들을 골라서 쓰게 되었을까요?

• 이 사람은 처음에 2가지 주제에 대해서 쓰고 싶었을 것이다.
  • 1번 주제: 쿠키 🍪
  • 2번 주제: 상대방에 대한 관심(Attention)
  • 비중은 한 반반 정도? 50%는 쿠키에 대해, 50%는 관심에 대해.
• 일단 하나의 주제를 정하면, 그 주제에 따라서 쓰기 쉬운 단어가 정해진다.
  • 초코칩은 쿠키라는 주제에서 나오기 쉬운 말이다.
  • 보고싶어는 관심이라는 주제에서 나오기 쉬운 말이다.
• 다른 주제를 골랐더라면 단어가 달라졌을 것이다.
  • 만약에 피자를 골랐다면, 널 페퍼로니로 치즈로 입맛 버리게 만들고 싶어 라고 썼겠지!
    • 쿠키를 골랐을 때 초코가 나올 확률 > 피자를 골랐을 때 초코가 나올 확률
    • 피자를 골랐을 때 페퍼로니가 나올 확률 > 쿠키를 골랐을 때 페퍼로니가 나올 확률
• 결국 문서를 작성한다는 것은, 이런 식으로 이루어질 것이다.
  • 문서 내에서 어떤 확률에 따라 주제를 고른다.
    • 쿠키:50%, 관심: 50%, 피자 0%
  • 주제는 각각 어떤 확률에 따라서 단어를 고른다.
    • 쿠키라는 주제에 대해 각 단어가 등장할 확률은 초코칩: 40%, 충치: 10%, 페퍼로니 0% ….
  • 2개의 과정을 거쳐 만들어진 단어의 집합이 하나의 문서가 된다.

문제는 이 모든 과정이 잠재적이라는 것입니다.

이렇게 ‘문서를 쓰게 된 과정’을 상상해봤지만, 사실 우리는 이 과정의 세부 디테일을 모릅니다. 쿠키 50%, 관심 50% 이런 정보는 문서 어디에도 써있지 않으며 우리가 알 수 있는 건 그 과정의 결과물인 단어들 뿐입니다. 즉 지금 우리가 해야 하는 것은 단어들을 보고, 미지의 확률값들을 추론하는 것입니다. (숨기고 있지만 널 더 보고 싶어!)

그래서 우리에게 필요한 것은 기본적으로 베이지안 추론입니다. 베이지안 추론은 간단하게,

• 궁금한 사건에 대해 잘 모르지만 일단 특정 확률에 따라 발생한다고 믿어본다.(사전 확률 분포)
• 사건을 관측해서 추가적인 정보를 얻는다.
• 얻은 정보에 더 들어맞도록 내 가정을 수정한다. (사후 확률 분포)

밑에서 더 자세히 살펴보겠지만 LDA가 바로 이런 방식으로 동작합니다. 여기서 관심 있는 사건이 문서이고, LDA는 주어진 문서가 가장 나올 법한 확률 분포를 찾아가는 과정이죠.

• 왠지 이 문서는 피자에 대한 것일 것 같아. → 앗 피자 관련된 말이 하나도 안 나왔어. → 피자에 대한 문서는 아닐 수도 있겠군.

이렇게 보면 나름 자연스러운 추론 과정이죠? 문제는 대충 ‘~에 대한 것일 것 같아’가 아니라 숫자로 된 파라미터를 가진 ‘확률 분포’가 필요하다는 것입니다. 그래서 이 때 다음 단어가 등장합니다.

디리클레

디리클레는 확률 분포의 이름입니다. 결론부터 말하면 디리클레 분포는 다항분포의 사전 켤레 분포이기 때문에 사용됩니다. 뭔 소리인지 모르겠으므로 풀어서 설명해 보겠습니다.

일단 다시 우리의 잠재적 가정으로 돌아가서, 주제가 정해졌을 때 단어를 고르는 상황을 상상해 봅시다. 주머니에 수많은 단어카드가 들어 있는데, 각 단어카드가 몇개씩 들어 있는지는 주제별 단어 분포에 따라 다를 것입니다. 주머니에 손을 넣어 아무 카드나 뽑는 걸 반복합니다. 독립적 시행이며, 같은 단어는 여러 번 반복해서 나올 수 있습니다.

이런 경우, 단어를 뽑은 결과는 다항분포를 따르지 않을까 생각해볼 수 있습니다. 다항분포의 확률질량함수(정해진 확률 파라미터에 따라 주어진 관측 결과가 나올 확률값을 돌려주는 함수라고 생각하면 됩니다)는 이렇게 생겼습니다.

\[f(x_1, \dots, x_k ; n, p_1, \dots , p_k) = \frac{n!}{x_1! \dots x_k!} p_1^{x_1} \dots p_k^{x_k}\]

• $k$개의 단어가 있고, 각 단어가 나타날 확률이 각각 $p_1$, … $p_k$로 정해져 있을 때 , $n$번을 뽑았을 때 단어가 $x_1$, …, $x_k$개씩 나타날 확률은 위와 같다. ($p$는 확률이므로 $p$를 다 더한 값은 1이며, $x$를 다 더한 것은 $n$일 것.)
• 쉽게 말하면 다항분포는 주사위 10번 던졌는데 1이 3번, 4가 7번 나올 확률은 어떻게 돼? 라는 질문에 대한 답을 주는 분포다. 이 경우 모든 $p$가 1/6이고, $n$이 10이고, $x$는 (3,0,0,7,0,0)이므로 저 식에 따라서 확률을 계산할 수 있다.

하지만 앞서 언급했듯 우리는 확률값을 전혀 모르기 때문에 사전 확률을 정한 다음 업데이트를 통해 사후 분포를 얻는 전략을 취할 겁니다. 그래서 사전 확률 분포를 뭐로 정할 것이냐의 문제인데요. 사전 확률 분포와 사후 확률 분포가 같은 가족군일 때 이들을 켤레분포라고 하며, 만약에 켤레 사전 분포(conjugate prior)를 사전 분포로 사용할 경우 사후 분포 업데이트에 필요한 계산이 매우 편해지기 때문에 켤레 사전 분포를 사전 분포로 고르게 됩니다.

• ❓ (참고) 켤레 사전 분포
  • 만약 단어가 2개밖에 없다면 → 이항분포(Binomial)
    • 이항분포의 켤레 사전 분포는 베타 분포
  • 단어가 여러 개이면 → 다항분포(Multinomial)
    • 다항 분포의 켤레 사전 분포는 디리클레 분포

다항분포의 켤레 사전 분포인 디리클레 분포를 살펴 보기 전에, 왜 따로 사전 분포가 필요한데? 사후 분포랑 뭐가 다른데? 라는 생각을 해보면,

• 다항분포는 각 사건의 확률 정보를 파라미터로서 알고 있어야 한다. 즉 각 단어가 나올 확률을 안다고 가정하고, 그 설정 하에서 최종 관측치(문서)의 확률을 알 수 있게 된다.
  • p( 관측치 | 확률 정보)
  • 주사위를 던지는데 각 숫자가 나올 확률은 1/6인데 이런 관측치가 나올 확률은?
• 디리클레 분포는 이걸 거꾸로 한 것. 우리가 아는 건 최종 관측치(문서)일 뿐이므로, 문서가 주어졌을 때 각 단어의 확률이 어떨지를 나타내주는 함수이다. 관측치가 파라미터다.
  • p( 확률 정보 | 관측치 )
  • 주사위를 던지는데 이런 관측치가 나왔는데 각 숫자가 나올 확률은?

디리클레 분포의 확률밀도함수는 이렇게 생겼습니다(다항분포와 달리 연속확률분포입니다).

\[f(p_1, \dots, p_k ; \alpha_1, \dots, \alpha_k) = \frac{1}{ B(\alpha)} \prod_{i = 1}^k p_i^{\alpha_i-1}\] \[B(\alpha) = \frac{\prod_{i=1}^{k} \gamma (\alpha_i)}{\gamma (\sum^k_{i=1} \alpha_i)}\]

• 우리가 관측하기로 총 $k$개의 단어가 있고, 각각 $\alpha$ 번씩 등장했을 때, 이 함수는 각 단어가 등장할 확률이 $p$일 확률값을 돌려준다. (역시 모든 $p$의 합은 1)
• $B(\alpha)$는 $\alpha$ 값과 감마함수에 따라 결정되는 정규화 상수다.

이해를 위해 단어가 3개 있다고 가정할 때 $\alpha$ 값에 따라 확률밀도함수가 어떻게 달라지는지 보겠습니다.

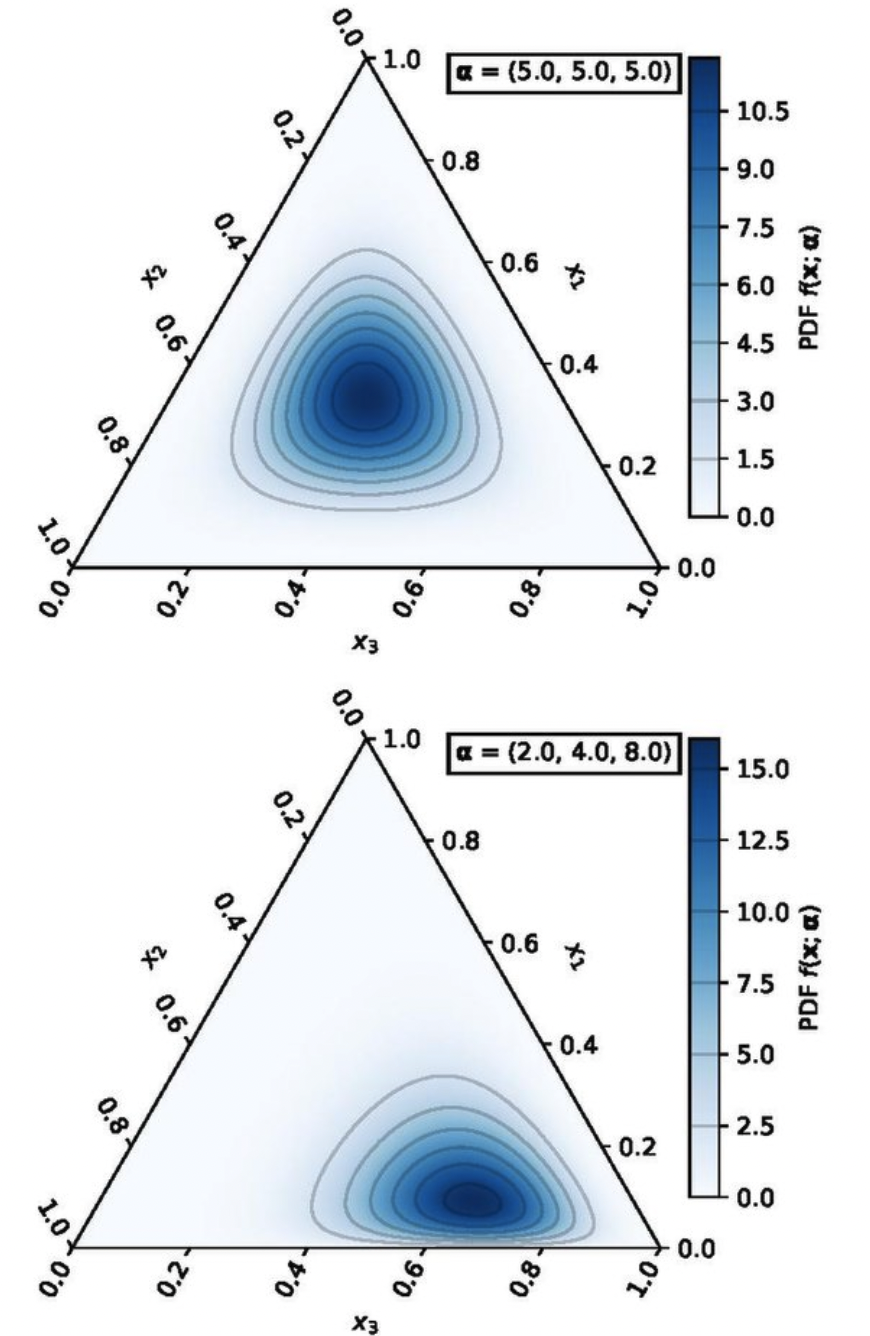그림 출처

• 위: 3개가 모두 동일한 횟수로 (5번씩) 나왔는데 각 단어가 등장할 확률은 아마 비슷하겠지?
• 아래: 세번째 단어가 8번 나오는 동안 첫번째, 두번째 단어는 2번, 4번 나왔는데 3번째 단어가 나올 확률이 제일 높겠지?

이제 LDA가 가정하는 잠재적인 과정과 이용하는 확률 분포에 대해 알았습니다. 마지막 단어로 넘어가서, LDA가 실제로 어떻게 주제를 찾는지 알아보겠습니다.

할당

LDA의 최종 목표는 단어별로 문서별로 주제를 할당하는 것입니다. 어떻게 할까요? 그 과정은 다음과 같이 하나의 도식으로 나타낼 수 있습니다.

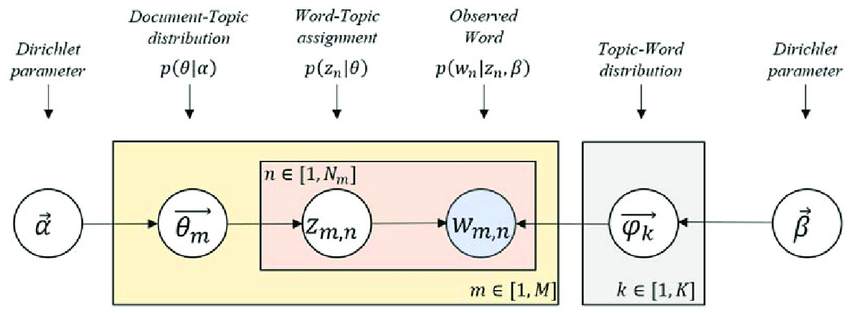그림 출처

• 2개의 분포가 있다.
  1. 문서마다 있는 주제 분포 (Document-Topic distribution)
     • $M$개의 문서가 존재 (분포도 $M$개!)
     • $\theta_m \sim \text{Dir}(\alpha)$ : $\alpha$ 라는 파라미터를 지닌 디리클레 분포를 사전분포로 쓰겠다는 뜻.
       • $\theta$는 그 문서에서 주제에 대한 확률값 벡터가 된다. ex) 쿠키:50%, 관심: 50%, 피자 0%
  2. 주제마다 있는 단어 분포 (Topic-Word Distribution)
     • $K$개의 주제가 존재 (분포도 $K$개!)
     • $\varphi_k \sim \text{Dir}(\beta)$ : $\beta$라는 파라미터를 지닌 디리클레 분포를 사전분포로 쓰겠다는 뜻.
       • $\varphi$ 는 그 주제에서 단어에 대한 확률값 벡터가 된다. ex) 초코칩: 40%, 충치: 10%, 페퍼로니 0% ….
• 관측된 단어(Obsered Word)에 주제를 할당(Word-Topic assignment) 해보자.
  • $N$개의 단어가 존재
  • 각 문서에 존재하는 관측된 단어 $w_{m,n}$ 에 대해 주제 $z_{m,n}$을 정해보자.
  • 두가지 분포의 결합으로 단어가 나타난다. 즉 단어의 결정은 문서-주제 분포로 결정된 주제($z$)와 그 주제의 주제-단어 분포를 결정하는 파라미터($\beta$)의 영향을 받는데,
    • $p(w_n \mid z_n, \beta)$
    • 이 확률이 컸으면 좋겠다 = 이 확률이 커지는 주제를 할당하고 싶다.
    • 이 추론 방식을 풀어 쓰면, 초코칩이라는 단어가 나타난 것은 이 문서가 쿠키라는 주제가 높은 확률로 등장하는 분포이기 때문에, 쿠키라는 주제는 초코칩이 높은 확률로 등장하는 분포이기 때문에… 이 ‘때문에’가 말이 되려면 이 여러 개의 변수 중 우리가 모르는 값들을(사실 $w$ 빼고 다 모름) 관측된 사건의 확률을 크게 해주는 방향으로 설정해주면 된다. 결국 단어에 주제를 할당할 때 목적은, 우리가 가정한 분포와 잠재적 과정이 우리가 실제로 관측한 단어를 최대한 잘 설명할 수 있도록 하는 것.

LDA는 이 목적을 달성하기 위해 베이지안 통계에서 자주 등장하는 깁스 샘플링(Gibbs Sampling)이라는 기법을 사용합니다. 단어의 개수가 많아질수록 우리가 추정해야 하는 값들의 차원이 엄청나게 늘어나기 때문에 추론에 필요한 계산을 가능하게 해주는 방법입니다.

전체 과정을 순서대로 설명하면 다음과 같습니다. 토픽의 개수인 $K$는 미리 지정해 주어야 합니다. 사전분포의 파라미터 값들($\alpha,$ $\beta$)도요.

1. 모든 단어에 아무 주제나 할당한다. 그러면 이 값에 따라 우리의 관심사인 2개의 분포가 결정된다.
   • 아무렇게나 정했기 때문에 당연히 엉망일 것이다. 이제 업데이트를 하자.
2. 1개의 단어를 고르고, 이 1개의 단어를 제외하고 나머지 단어들은 다 정답인 주제로 배정되어 있다고 가정한다.
   • 나머지 단어들만 사용해서 이 문서의 주제 분포와 각 주제의 단어분포를 다시 계산한다.
   • 이 분포를 기반으로 이 1개의 단어에 각 주제가 할당될 확률을 계산한 후 $p(z_i \mid z_{-i}, w)$ 가장 확률이 높은 주제로 재할당한다.
     • P(주제 $\mid$ 분포) x P(단어 $\mid$ 주제) 를 나머지 단어들의 카운트를 통해 계산하면 된다. 지금까지 설명한 단어 선정 방식과 직관적으로 일치하는 내용.
3. 문서 내 모든 단어에 대해 이것을 반복한다. 이것이 1회의 깁스 샘플링이다.
4. 샘플링(재할당)을 반복하다보면 더 이상 변동이 없이 안정적으로 수렴하는 순간이 올 것이다. 거기서 멈춘다.
5. 멈췄을 때 얻은 모든 단어의 주제 분포를 사용해서 단어의 집합인 각 문서에 주제를 할당한다.

참고한 글들

• Topic Modeling, LDA
• 잠재 디리클레 할당 파헤치기 2. 디리클레 분포와 LDA