Label Propagation Algorithm

Label Propagation Algorithm은 라벨이 부족할 때 유용한 준지도학습 테크닉이자 대규모의 그래프에 적용 가능한 쉽고 빠른 커뮤니티 탐지 기법이기도 합니다. 이 글에는 LPA 뜯어보기, 넘파이로 구현하기, 그리고 해리 포터 시리즈의 등장인물 네트워크 속 커뮤니티 탐지해보기 등의 내용이 포함되어 있습니다.

그래프 기반의 준지도학습(Semi-supervised Learning)

흔히 지도 학습이라 불리는 머신러닝 기법들은 일반적으로 모델 학습을 위해 라벨이 있는 데이터를 필요로 합니다. 그러나 현실에서 완벽하게 라벨링된 데이터를 구하기는 쉽지 않고, 대량으로 얻으려면 그만큼의 비용이 들기 마련입니다. 라벨 전파 알고리즘 (Label Propagation Algorithm) 은 이런 상황에서 사용할 수 있는 그래프 기반의 준지도학습 테크닉으로, 일부 라벨링 된 데이터 포인트로부터 라벨링되지 않은 다른 데이터 포인트들로 라벨을 전파해 나갑니다.

그냥 ‘전파’라고 하니까 뭘 어떻게 한다는 건가 싶은데, 사실 이 알고리즘의 아이디어는 아주 간단합니다: 저는 하와이안 피자를 좋아하는데(라벨 있음), 친구 A가 하와이안 피자를 좋아하는지는 아직 모릅니다(라벨 없음). 그런데 이 친구가 저와 다른 입맛과 취향이 매우 비슷하다면(그래프에서 가까움) 얘도 저처럼 하와이안 피자를 좋아하지 않을까요(전파)?

즉 라벨 전파란, 그래프(+소수의 라벨 있는 데이터)를 가지고 라벨이 없는 데이터의 라벨을 예측해 나가는 것을 의미합니다.

어떻게 하는 건지 좀 더 살펴보도록 하겠습니다.

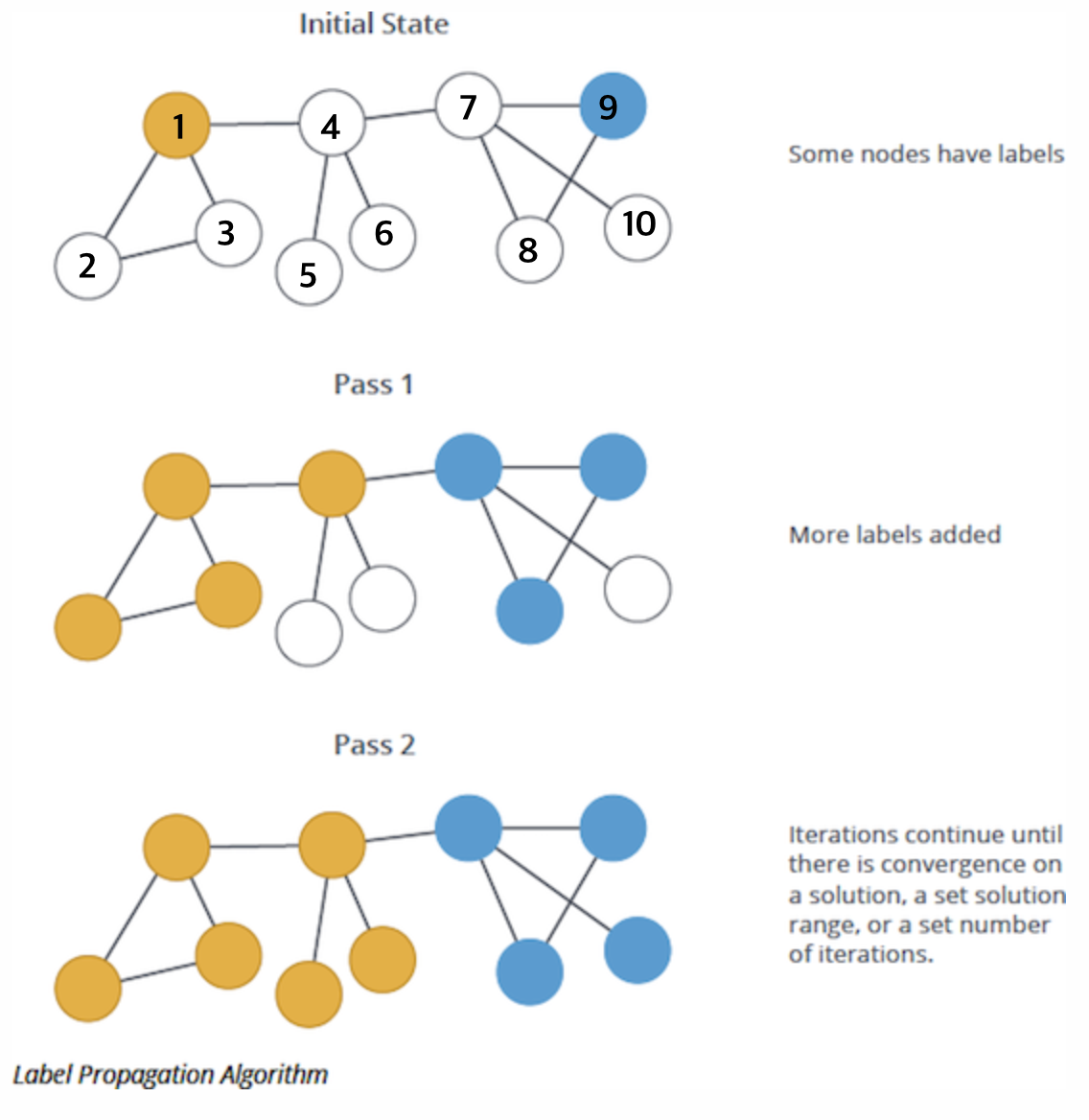이미지 출처

주어진 데이터 포인트들 $(x_1, y_1), \cdots, (x_n, y_n)$ 이 있고, 이중 일부는 라벨이 되어 있고 일부는 라벨을 모르는 값인 상황이라고 합시다. 즉 라벨값은 $Y_L = { y_1, \cdots, y_l}$ 이고, 나머지 $Y_U$는 비어 있습니다. 위 그래프의 경우에서는 (1, 노랑), (9, 파랑) 만 라벨이 있는 데이터인 거죠. 우리는 전체 $X$와 $Y_L$ 을 가지고 $Y_U$를 알아내야 하는 것입니다.

그러기 위해서 우선 유클리디언 거리를 통해 X의 인접행렬(adjacency matrix)을 계산할 겁니다. 인접 행렬의 각 원소는 이런 식으로 계산됩니다. ($x_i$와 $x_j$가 얼마나 가까운지 나타내는 일종의 유사도 값이라고 생각하면 됩니다. 가까울 수록 $w_{ij}$ 값은 커집니다. 사전 지정한 파라미터 $\sigma$가 필요합니다.)

\[w_{ij} = \exp (-\frac{\sum^D_{d=1} (x_i^d - x_j^d)^2}{\sigma^2})\]

그리고 이 인접 행렬을 가지고 다음과 같은 확률적 전이 행렬(Probabilistic transition matrix)라고 불리는 $T$를 얻습니다. 수식을 보면, 위 인접 행렬을 전체 합을 가지고 정규화한 값인 걸 알 수 있을 거예요.

\[T_{ij} = P(j \rightarrow i) = \frac{w_{ij}}{\sum_{k=1} w_{kj}}\]

두 행렬의 의미는 이렇습니다.

• $w_{ij}$ : $x_i$와 $x_j$ 사이의 거리가 가까울수록 커지는 가중치 값
• $t_{ij}$: $w_{ij}$를 $x_j$에 연결된 모든 노드의 가중치 값을 더해 나눠준 값
  • 즉, 가중치에 따라 노드를 선택하는 랜덤 워크를 돌릴 때 $x_j$에서 $x_i$로 넘어갈 확률!

현 상태의 라벨에 이 행렬 $T$를 곱해서 새로운 라벨 $Y$로 만드는 것을 ‘1번 라벨을 전파’한다고 봅니다. 즉 한 노드에서 다른 노드로 넘어갈 확률에 맞게 라벨을 넘겨주는 개념이라고 보면 됩니다. 라벨 전파 알고리즘은 이 한 번의 이터레이션을 여러 번, 안정적인 라벨 $Y$가 나올 때까지(수렴할 때까지) 반복하는 과정입니다. 처음에 $T$를 만들 때처럼 정규화하기 때문에 매번 반복할 때마다, 그리고 수렴하고 나서도 $Y$의 값들은 각 노드가 각자의 라벨에 속할 확률 값의 의미를 지니게 됩니다. 수식을 작은 그래프 예시와 MATLAB 계산으로 잘 설명한 글이 있어, 읽어보면 상세한 이해에 도움이 될 듯합니다.

준지도학습 LPA는 사이킷런이 지원해 주고 있습니다. (유저 가이드 참고)

from sklearn.semi_supervised import LabelPropagation
from sklearn import datasets
label_prop_model = LabelPropagation()
iris = datasets.load_iris()
rng = np.random.RandomState(42)
random_unlabeled_points = rng.rand(len(iris.target)) < 0.3
labels = np.copy(iris.target)
labels[random_unlabeled_points] = -1
label_prop_model.fit(iris.data, labels)

위 예시는 붓꽃 데이터를 가져와 랜덤으로 라벨을 없앤 다음, LPA를 통해 라벨을 전파하는 코드입니다.

어, 그런데 붓꽃 데이터는 원래 그래프가 아니죠? (모르는 분들을 위해: 붓꽃 데이터는 3가지 품종의 붓꽃으로 분류하기 위해 각 꽃의 꽃잎과 꽃받침의 길이를 이용하는 전형적인 지도학습 모델 연습용 데이터입니다.)

여기서 주의할 점은 이 사이킷런 메서드는 일반적으로 지도학습 모델에 인풋으로 넣는 피쳐들로 구성된 데이터를 받는다는 것입니다. 즉 붓꽃 데이터처럼 수치형 데이터를 받아서 자동으로 거리/유사도 계산을 해서 그래프를 만든 다음에 LPA를 적용해 줍니다! 아주 편하죠.

하지만 만약 내가 가지고 있는 게 그래프뿐이라면? 슬프게도 저걸 못 씁니다. 당황하기 시작합니다… 는 바로 네트워크 데이터에 써보고 싶었던 제 상황이었습니다. 그래서 하는 김에 그래프 데이터와 거리 행렬에 바로 사용할 수 있도록 numpy로 만들어 봤어요.

def label_propagation_with_graph(adjacency_mat, label_vec, max_iter=500, diff=1e-3):
  labels = np.unique(label_vec)
  labels = labels[labels!=-1]
  label_n = labels.shape[0]
  node_n = len(adjacency_mat)
  already_labeled = np.where(label_vec != -1)
  not_labeled = np.where(label_vec == -1)
  
  #원핫인코딩 행렬 얻기
  label_vec[not_labeled] = 0
  encoding = np.eye(label_n)[label_vec]
  encoding[not_labeled] = 0

  #인접 행렬 정규화
  degs = np.sum(adjacency_mat, axis=1)
  degs[degs==0] = 1
  adjacency_mat = adjacency_mat / degs
  
  now_pred = encoding
  prev_pred = np.zeros( [node_n, label_n] )
  
  #정해진 범위(max_iter) 만큼만 돌되,
  #그 전에 변동이 일정 수준(diff) 이하로 내려가면 멈추기
  for i in range(max_iter):
    if np.sum(np.abs(now_pred - prev_pred)) < diff:
      break

    prev_pred = now_pred    
    #전파하기. 단 원래 라벨 있었던 애들은 바뀌면 안됨!
    now_pred = np.dot(adjacency_mat, now_pred)
    now_pred[already_labeled] = encoding[already_labeled]
    
  
#결과는 각 라벨에 해당될 확률 행렬 / 확률이 제일 높은 걸 최종 라벨로 결정한다.  
  return now_pred, np.argmax(now_pred,1)

우리에게 붓꽃 원본 데이터가 없고, 붓꽃 데이터 간 인접 행렬, 즉 그래프 데이터만 있다고 가정해 봅시다. (사실은 원본 데이터에서 만들어서 쓸 거지만!)

from sklearn.metrics.pairwise import rbf_kernel 
adj_mat = rbf_kernel(iris.data) #RBF 커널을 사용해 인접 행렬 계산

#인접 행렬과 (일부만 남긴) 라벨을 가지고 위 Label Propagation 함수를 적용할 수 있다
result_p, result_l = label_propagation_with_graph(adj_mat, labels)

잘 작동하나 봅시다. 아래는 순서대로 다음 3가지 입니다.

• 원래 라벨 (iris.target)
• 랜덤하게 뽑아서 라벨을 지운(-1로 만든) 라벨
• LPA 진행 후 전파된 라벨

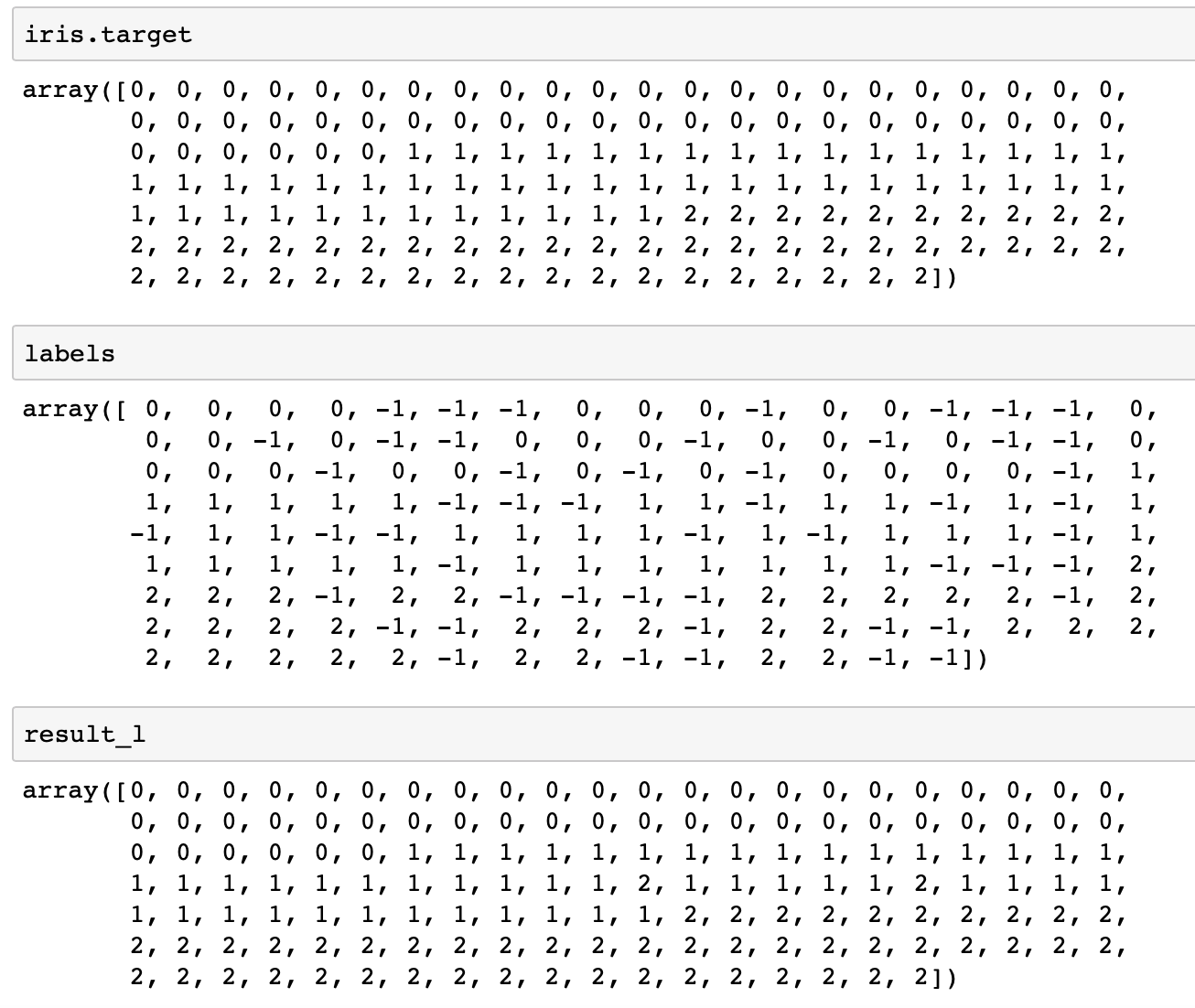인접 행렬을 이용해서 가까운 라벨 있는 데이터에서 전파시킴 → 대부분 원래 라벨을 되찾았다!

네트워크 커뮤니티 탐지

비슷한 아이디어를 커뮤니티 탐지에도 이용할 수 있습니다.

(잠깐) 커뮤니티 탐지(Community Detection)란, 전체 네트워크 상에서 긴밀하게 연결된 노드들의 하위 집합을 도출하는 네트워크 분석 방식입니다. 커뮤니티의 정의는 연구마다 기법마다 조금씩 다를 수 있습니다.

커뮤니티 탐지를 위한 LPA는 Near linear time algorithm to detect community structures in large-scale networks 에서 처음 제안되었습니다. 이 방법은 A라는 노드에 대해, A가 어떤 커뮤니티 속하는지를 보려면 A 주변 노드들이 어떤 커뮤니티에 속했는지를 보자는 접근입니다. A 주변 노드들이 다 X라는 커뮤니티에 속해 있다면 A도 X에 속해 있을 확률이 높다는 것인데요. 뭐 그냥 라벨 = 커뮤니티로 바꿔서 위에서 한 거랑 비슷한 소리를 또 하고 있는 것 같죠?

자세히는 이런 식입니다.

1. 처음 시작할 때 t=0 모든 노드들은 각자의 고유한 라벨을 지닌다. 즉 모든 노드 $\mathbf{x}$ 에 대해 $C_\mathbf{x}(0) = \mathbf{x}$.

2. t=1부터 모든 노드들에 랜덤한 순서를 배정한다. 이 순서 리스트를 $X$라 하면, 특정 순서를 가지는 $\mathbf{x} \in X$에 대해,

   \[C_{\mathbf{x}} (t) = f ( C_{\mathbf{x}_{i1} }(t), \cdots , C_{\mathbf{x}_{im}} (t), C_{\mathbf{x}_{i(m+1)}} (t-1), \cdots, C_{\mathbf{x}_{ik}} (t-1) )\]
   • $f$는 각 노드의 주변 노드 중에서 가장 빈도가 높은 라벨을 돌려주는 함수다. 만약 동점이 있을 경우 그냥 랜덤하게 뽑는다.
3. 모든 노드가 유일하게 최빈 라벨로 결정되면 반복을 멈춘다. 그렇지 않다면 t = t+1, 2번 단계로 돌아가 반복한다. 커뮤니티 라벨이 어떻게 전파되는지 직관적으로 이해할 수 있게 해주는 그림 (논문 figure2)

이 방식의 장점은 우선 속도입니다. 이 알고리즘의 각 이터레이션의 시간복잡도는 $O(n)$으로, 그래프의 엣지의 수에 따라 선형적으로 증가합니다. 다른 널리 알려진 커뮤니티 탐지 방법들이 모듈성(modularity)이라는 지표를 매번 계산하기 때문에 계산 비용이 높은 반면( $O(n \log n)$ 또는 $O (m+n)$ ) , LPA는 따로 지표 값을 계산할 필요가 없답니다.

또 아이디어가 간단하고 매우 직관적이기 때문에 형성된 커뮤니티의 결과를 설명하거나 해석하기도 좋습니다.

그러면 이제 빠르게 한 번 써먹어 보겠습니다.

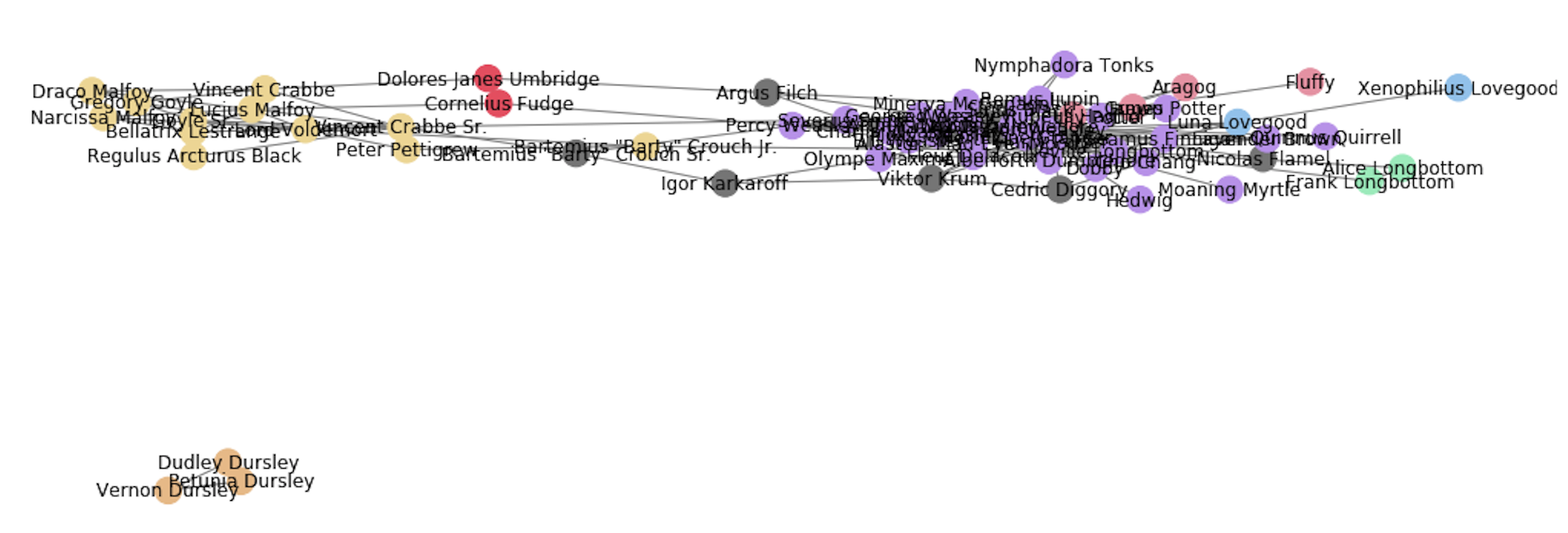
해리 포터가 속한 커뮤니티는? 👓 ⚡️

오늘의 예시 데이터는 해리 포터 시리즈의 등장인물들 간의 관계 네트워크입니다. (👉 데이터 출처는 여기!)

해리포터의 등장인물간 관계를 긍정적(+)인지 부정적(-)인지로 표현한 데이터인데요, 그대로 쓰면 너무 모든 인물들이 다 연결된 경향이 있어서 저는 긍정적인 관계만 필터링하여 엣지로 그래프를 만들겠습니다.

import networkx as nx

G = nx.from_pandas_edgelist(positive_relations, source='source_name',target='target_name')
print(nx.info(G))

총 64명 & 224개의 긍정 관계

networkx가 지원하는 LPA는 다음과 같이 간단하게 해볼 수 있습니다.

lpa_communities = nx.algorithms.community.asyn_lpa_communities(G)

참고로 위 메서드는 처음 LPA 커뮤니티 탐지를 제안한 원 논문에서 제안한 asynchrous한 방법입니다. 이후 등장한 semi-synchronous한 방법(논문: Community Detection via Semi-Synchronous Label Propagation Algorithms)도 구현이 되어 있는데요, 이 방법은 아예 처음부터 라벨 전파를 하는 것이 아니라 노드 컬러링(node coloring)을 통해서 그룹별로 나눠서 전파를 함으로써 속도와 안정성을 개선했다고 합니다.

Semi-sync 버전은 이렇게 합니다.

lpa_communities = nx.algorithms.community.label_propagation_communities(G)

소스 코드를 보면 어떻게 돌아가는지 더 자세한 내용을 볼 수 있어요.

커뮤니티 탐지 결과를 nx.draw로 그려봅니다. 같은 커뮤니티는 같은 색의 노드로 표현했고, 1개의 구성원만 있는 커뮤니티는 미분류로 보고 회색으로 칠해봤어요.

전반적으로는 2개의 큰 커뮤니티로 분화되어 있는 것이 보이고요. 그 2개는 (왼쪽의 노란색) 볼드모트와 죽음을먹는자들 ↔ (오른쪽의 보라색) 해리 포터의 친구들입니다. 아마 기숙사 통계도 빤할 테니 왼쪽은 초록색으로 오른쪽은 빨간색으로 칠할 걸 그랬죠? 새삼 마법사 세계가 상당히 이분법적이었음을 느낍니다… 사용한 데이터가 단순한 탓도 있긴 하지만요.

밀집된 부분의 이름은 잘 안 보이지만, 주인공 삼인방을 포함 대부분의 악역 아닌 주요 인물들은 당연히 보라색 커뮤니티에 포함되어 있습니다. 보라색 커뮤니티 구성원은 무려 31명으로, 전체 노드 중 거의 절반에 달하는 숫자입니다.

그 외 소규모 커뮤니티에서는 마법부, 더즐리 가족(외딴 머글 섬), 해그리드와 괴물 친구들, 러브굿 부녀 등이 눈에 띕니다. 간혹 얘가 왜 여기? 하는 노드들도 있지만 이런 그룹을 보면 제법 잘 묶인 것 같아요.

또 몇 번 돌려보니, 처음에 방문할 노드를 랜덤 순서로 섞는 것 때문에 돌릴 때마다 매번 커뮤니티 결과가 상당히 다르게 나오는 것을 실감했습니다. 기본적인 큰 커뮤니티(그림상 노란색/보라색)의 틀은 계속 유지되었지만 작은 커뮤니티들은 계속 바뀌면서 없어지거나 이상하게 묶이거나 다른 커뮤니티에 붙거나 하더라고요. 아무 노드에서나 출발해서 계속 돌면서 라벨을 바꾸는 방식의 알고리즘이기 때문에 그렇습니다.

✨ 보너스) 스파크에서도 쉽게 쓸 수 있다

애초에 LPA를 업무에서 써보고 싶어서 알아본 거였는데 스파크 환경에서도 graphframes가 지원을 해주더라고요. 제가 찾아본 바로는, Louvain이나 Girvan-Newman 처럼 다른 modularity 기반의 커뮤니티 탐지 방식들은 graphframes에는 없어서 따로 구현이 필요합니다. 그래서 만약 스파크로 커뮤니티 탐지를 하고 싶다면 LPA가 가장 편한 옵션으로 보입니다.

우선 graphframe을 생성해주고, 다음과 같이 LPA를 적용하면 됩니다.

from graphframes import *
G = GraphFrame(nodes, edges)
communities = G.labelPropagation(maxIter=5) #max iteration 설정가능해서 좋다!

networkx는 max iteration 설정 없이 그냥 모든 노드 라벨이 변동이 없을 때까지 돌게 되어 있는데, graphframes는 최대 반복 가능한 이터레이션을 파라미터로 설정할 수 있습니다. 디폴트 값은 5이고요. 업무 데이터 중 노드가 몇만 개 정도 되는 그래프에 적용해 봤는데요, 이터레이션을 너무 키우면 가장 큰 커뮤니티가 더욱 더 커지는(다 거기로 흡수되는) 현상이 일어나서 유의미한 결과로 보기 힘들었습니다. 5로 하는 게 가장 나았고, 원 논문에서도 테스트 결과 전체 노드의 95% 이상이 5번 안에 바르게 분류가 되었다고 합니다.

참고

• Learning From Labeled and Unlabeled Data With Label Propagation → LPA for Semi-Supervised Learning 논문
• Label Propagation Demystified
• How to get away with few Labels: Label Propagation
• Near linear time algorithm to detect community structures in large-scale networks → LPA for Community Detection 논문
• [도서] 그래프 알고리즘 6장. 커뮤니티 검출 알고리즘
• Large-scale Graph Mining with Spark: Part 2
• [네트워크이론] Label propagation algorithm for community detection