아직도 커널이 뭔지 모르겠어요
여기저기서 등장하는 커널(Kernel)이란 개념을 쉽게 이해하고자 정리한 내용입니다. 커널 밀도 추정, 커널 회귀, 커널 SVM을 다룹니다.
학습을 할 때, 공통적인 개념이 존재하는데 개념이 아닌 응용부터 배우다 보니 각 응용법이 개별적으로만 인식이 되고, 공통적인 개념 기준으로는 머릿속에서 잘 끼워맞춰지지가 않을 때가 있습니다. 저에겐 바로 커널(Kernel) 이라는 단어가 그랬습니다. 지금까지 머신러닝 공부를 하면서 참 여기저기서 많이 들어본 단어인데요. 상당히 익숙하고, ‘커널’이라는 단어가 붙은 모델이나 기법들을 대충은 이해하고 있음에도 불구하고, 그래서 커널이 정확히 뭔데? 라고 누가 물어보면 아무래도 대답을 못할 것 같다는 생각이 들었습니다.
그래서 오늘은 커널이 뭔지부터 시작해서 제가 커널이라는 단어를 들어봤던 ‘여기저기’를 한번 간단히 훑어 보려고 합니다.
그래서 커널이 뭔데
위키피디아에 커널이라고 쳐봤습니다.
결과는 좀 무섭습니다. Kernel may refer to: … 하고선 항목이 20개가 넘게 나옵니다. 제가 아직까지도 커널이 뭔지 정확히 모르는 건 애초에 개념이 너-무 많아서 그런 거라고 위안이 되기도 하네요.
우선 CS 영역에서 커널은 운영체제의 핵심 요소… 이 부분은 제가 알 필요가 없을 것 같습니다. 과학 분야에서는 씨나 원자핵을 의미한다는데 이것 역시 알 필요 없어 보입니다(참고로 kernel의 기본 정의는 씨앗, 알맹이, 핵이라고 하니 이게 가장 직접적인 쓰임새가 맞겠네요). 제가 봐야 하는 건 수학과 통계학에서의 커널이고, 몇 개를 눌러 보니 익숙한 그림이 몇 개 보이는 부분은 바로 Functions 항목, 그러니까 함수로서의 커널인 것 같아요. 즉 제가 알아야 하는 커널은 어떤 복잡한 개념이라기보단 특정 함수였던 것입니다.
하지만 함수라는 섹션 안에서도 항목이 10개나 있습니다! 커널은 정말 다용도 개념인 게 틀림없어 보입니다. 만약 사전을 읽어서 뜻을 파악하듯이 개념을 이해할 수 있었다면 개념 이해에서부터 먼저 출발하고 싶었지만, 솔직히 뭐부터 이해해야 하는지도 모르겠기 때문에 전략을 바꿔서, 제가 대충 이해하고 있었던 ‘커널 어쩌구’들을 커널이 뭔데? 라는 관점에서 다시 한번 보기로 했습니다.
커널 밀도 추정
첫번째 친구는 변수의 알려지지 않은 확률 분포를 추정하는 Kernel Density Estimation(줄여서 KDE)입니다.
우선 확률 분포 추정이란 게 무엇인지부터 간단히 짚고 넘어가겠습니다. 예를 들어 제가 피자를 만드는데, 그때의 기분이나 배고픔의 정도에 따라 도우의 크기가 매번 들쭉날쭉하다고 칩시다. 어떤 날은 10인치짜리 도우를 만들고 어떤 날은 16인치 도우를 만듭니다. 하지만 지난 몇 년 간 관찰을 해 보니, 일반적으로 16인치를 만드는 날이 10인치를 만드는 날보다 훨씬 더 많습니다. 이게 바로 분포적인 특성이죠. 하지만 얼만큼 많을까요? 즉, 내일 제가 16인치짜리 큰 피자를 만들 가능성은 어느 정도이고 그건 10인치짜리를 만들 가능성보다 얼만큼 높을까요? 이 질문들에 답을 할 수 있는 방법이 바로 피자 도우 크기의 확률 밀도 함수를 추정하는 것입니다.
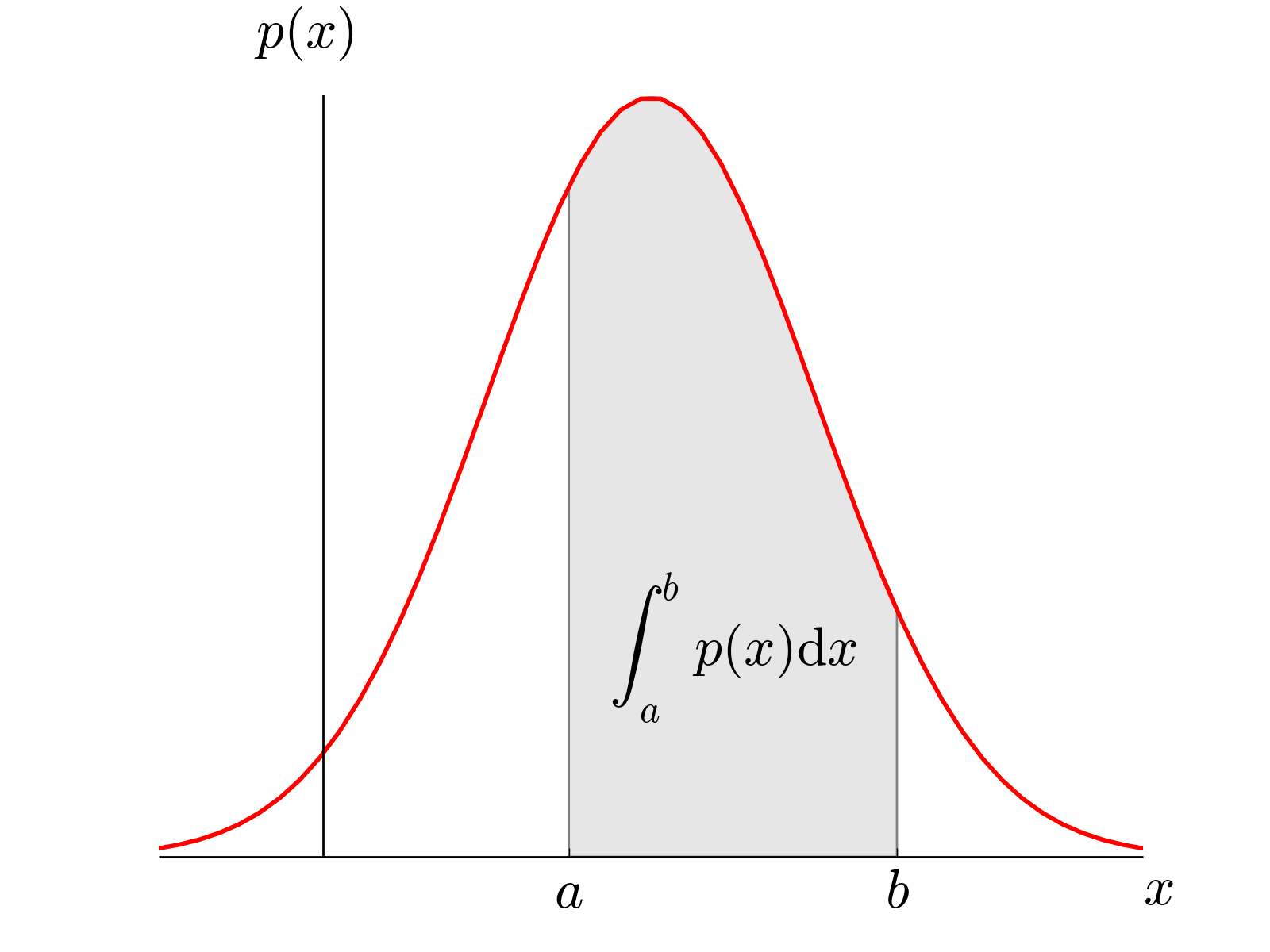
확률 밀도 함수(probability density function; PDF)는 연속형 변수인 $X$를 받아서 특정 값($x=a$)일 확률 밀도(density)값을 돌려주는 함수입니다. 밀도라는 개념이 직관적이지는 않은데, 여기서 밀도인 $\text{PDF}(x)$는 확률 값이 아니기 때문이에요. 다시 예시로 생각해 보면 알 수 있는데요, 피자 크기가 정확히 15인치일 확률은 어떻게 될까요? 제가 아니라 어떤 기계가 와도 정확히 ‘15인치’를 만들 수 없습니다. 도우의 지름이란 변수의 정의 자체가 연속적인 실수값이기 때문이죠. 따라서 $x=15$일 확률은 0입니다. 하지만 대충 ‘15인치 언저리’일 가능성을 상대적으로 나타낼 수는 있는데 그것이 바로 확률 밀도의 개념입니다. 또한 밀도 함수로부터 ‘15인치에서 16인치 사이’일 확률도 계산할 수 있는데, 그림처럼 a와 b 사이의 면적, 즉 PDF의 적분값을 계산하면 변수가 특정 구간의 값을 가질 확률이 됩니다.
제가 1년치 피자를 만든 기록을 가지고 이러한 확률 밀도 함수를 추정하고 싶다고 할 때 가능한 방법은 2가지가 있습니다.
- 특정 분포를 따른다고 가정하고, 주어진 데이터에 맞게 파라미터만 추정하기
- 사전 가정 없이 주어진 데이터만 가지고 추정하기
1번이 바로 모수적인(parametric) 추정 방식입니다. 정규분포를 따른다고 가정했다면 정규분포의 파라미터인 평균과 분산 값만 알아내면 됩니다. 하지만 현실적으로 봤을 때 대체 뭘 믿고 대뜸 그냥 이 변수는 이 분포를 따를 거야 라고 가정할 수 있을까요? 반면에 2번은 비모수적인(non-parametric) 방식이라고 부릅니다. 이처럼 주어진 데이터만 사용하고 분포를 알 수 있는 가장 간단한 방법은 히스토그램을 그리는 것입니다.
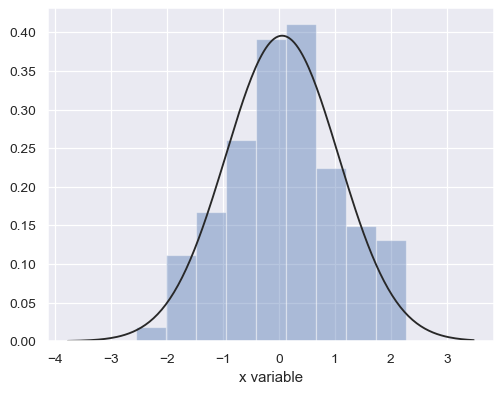히스토그램 (이미지 출처)
하지만 히스토그램의 문제는 보시다시피 불연속적이고, bin(막대/데이터를 카운트하는 기준 구간 길이)의 크기를 어떻게 설정하느냐에 따라 모양도 달라집니다. 우리가 하고 싶은 것은 이 히스토그램을 저 검은색 선처럼 연속적인 선으로 바꾸는 것입니다. 이때 커널 함수가 해결책으로 등장합니다.
여기서 사용되는 커널 함수 $K$는 다음 2가지 특징을 만족하는 non-negative 하고 적분 가능한 함수를 뜻합니다.
- 적분 값이 1이다. ( $\int_{-\infty}^{+\infty} K(u) du = 1$ )
- 원점을 기준으로 대칭이다. ($K(-u) = K(u)$ $\forall u$)
해당 조건을 만족하는 커널 함수에는 다음과 같이 많은 종류가 있습니다.
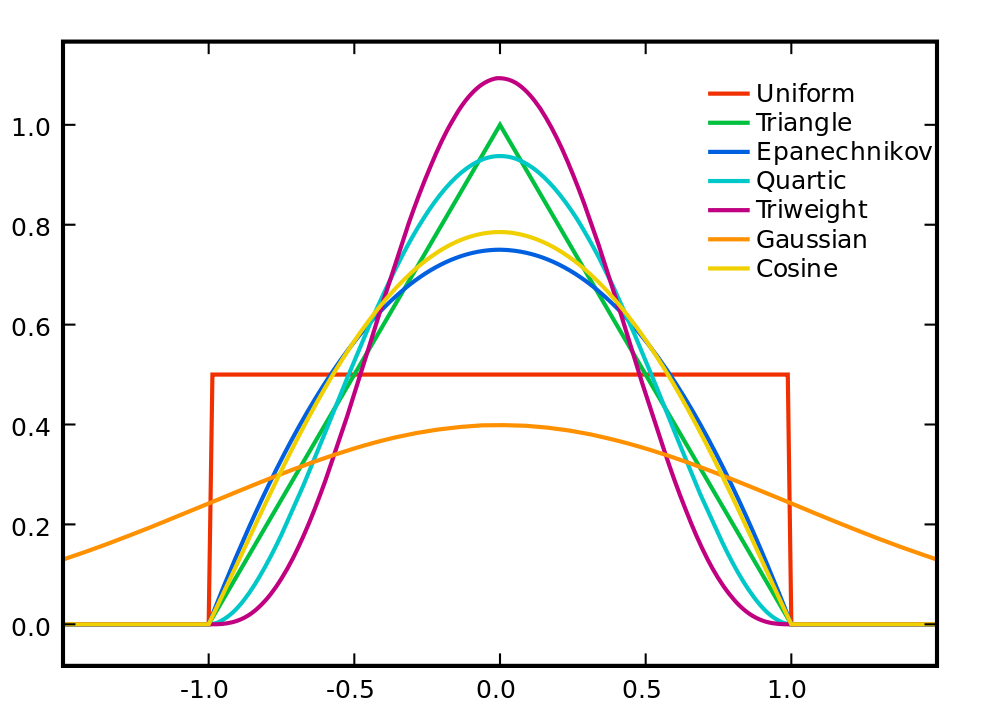다양한 커널 함수 (이미지 출처)
이런 함수 $K$를 다음과 같이 사용하여 히스토그램 대신 smooth한 밀도함수 $f(x)$ 를 얻는 것이 바로 KDE 기법입니다.
\[\hat{f_h} (x) = \frac{1}{n} \sum ^n _ {i=1} K_h (x-x_i) = \frac{1}{nh} \sum^n _{i=1} K (\frac{x-x_i}{h})\]수식을 살펴보면, 각 $x$값에 대해 다른 모든 $x$값과의 거리를 $h$라는 bandwith 파라미터로 조절된 커널 함수 $K$에 넣고, 이것을 모든 $x$값에 더한 다음 데이터의 개수인 $n$만큼 나눠주고 있습니다. bandwith $h$는 커널함수가 얼마나 뾰족해야 할지 조절하는 값입니다.
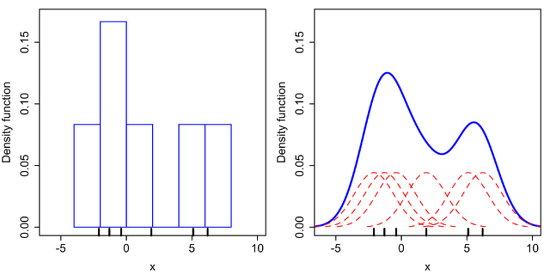히스토그램 → KDE (이미지 출처)
그림으로 보면 이해가 쉬울 것 같습니다. 오른쪽에서 커널 함수들(빨간색)이 많이 겹치는 구간일수록 데이터가 몰려 있다고 볼 수 있으므로 최종적으로 추정된 밀도 함수(파란색)에서는 확률 밀도 값이 높게 표현되는 걸 볼 수 있습니다.
- 거리 값을 넣는 이유: 각 $x$와 멀리 떨어진 다른 $x_i$ 에 대해서는 적은 값을 돌려주게 되도록 (위의 다양한 커널 함수 생김새를 보면 원점에 가까울수록 큰 값, 멀어질수록 작은 값)
- 즉 5 근처의 확률 밀도 값에 5와 멀리 떨어진 데이터들은 적게 기여하고 가까운 데이터들은 높은 가중치로 기여하도록 → 즉 어떻게 보면 $x$와 $x_i$의 가까운 정도(유사도)를 돌려주는 함수
- 데이터 개수로 나눠주는 이유: 확률 밀도 함수는 적분값이 1(모든 확률의 합은 1)이어야 하는데 커널 함수를 데이터 개수만큼 $n$번 더했으므로 마지막에 $n$으로 나눠줌
KDE에서 커널이란 비모수적 추정을 할 때 불연속적 분포를 smooth하게 표현하기 위해 사용되는 함수
커널 회귀
두번째는 Kernel Regression입니다.
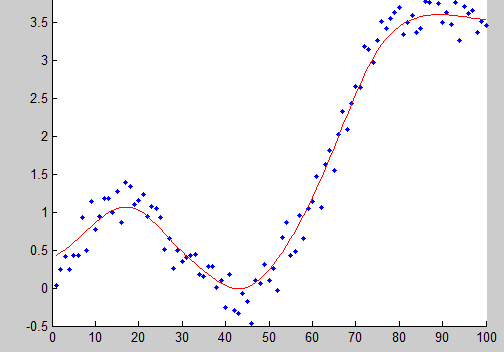
보다 우리에게 친숙한 선형 회귀(linear regression)의 경우, X와 Y의 관계가 선형일 것이라는 가정 하에 그 선형 관계의 양상을 나타내주는 파라미터를 데이터를 기반으로 추정하게 됩니다. 바로 모수적인 방법이죠. 반면 커널 회귀와 같은 비모수적인 방법은 별도의 가정 없이 주어진 데이터만 가지고 Y값을 예측하는 함수를 만들고자 합니다. 잘 된다면 다음과 같은 비선형적인 관계도 잘 표현할 수 있다는 장점이 있습니다.
이미지 출처
여기서 컨셉은 KDE와 비슷합니다. KDE에서 각 데이터포인트별로 나와 가까이 있는 다른 데이터들이 높은 값으로 반영되도록 커널 함수를 사용한 것처럼, 이번에도 Y를 예측할 때 가까운 값들에 높은 가중치를 둔 가중평균을 통해 예측을 하려고 합니다.
\[y_t = \frac{1}{n} \sum^n_{i=1} w_iy_i\]이때 가중치는 다음과 같이 커널 함수 $K$를 이용해서 계산합니다.
\[w_i = \frac{ K(x_t-x_i)}{ \sum ^n _ {i=1} K( x_t-x_i)}\]앞서 언급한 대로 $x_t$와 거리가 멀어질수록 높은 값을 돌려주는 커널 함수를 사용하게 되므로, $x_t$와 가까운 데이터포인트일 수록 $y_t$에 높은 가중치를 두어 합하게 됩니다. 이와 같은 방식을 통해 KDE에서처럼 저런 smooth한 예측 함수 선을 만들어낼 수 있습니다.
커널 회귀에서 커널이란 가까운 데이터들의 가중평균을 통해 예측 변수를 예측할 때 가중치 값으로 사용되는 함수
커널 SVM
두번째는 Kernel Support Vector Machine입니다.
이미지 출처
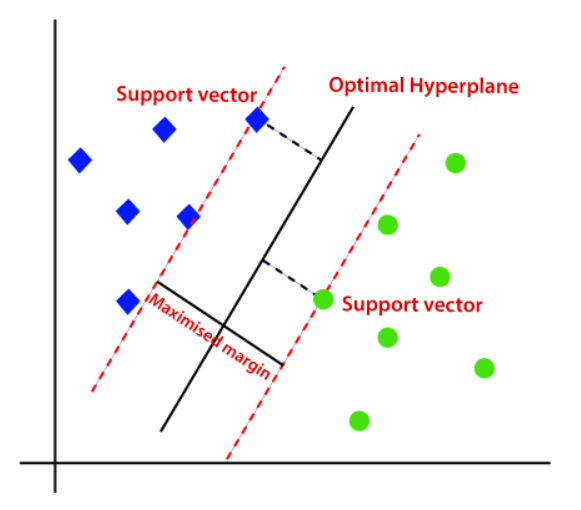
Support Vector Machine(SVM)에 대한 간단한 요약부터 하겠습니다. SVM은 분류 과제에서 쓰일 수 있는 지도학습 모델 중 하나로, 분류를 위한 최적의 결정 경계선을 찾고자 합니다. SVM이 ‘최적’이라고 생각하는 경계선은 경계선과 가장 가까이 있는 데이터들로 이루어진 서포트 벡터와 경계선 사이의 거리(마진)가 최대화되는 경계선입니다. 이 경계선을 찾는 문제는 라그랑지안 승수 $\alpha$에 대해 다음과 같은 목적 함수로 정의됩니다.
\[\max L_D(\alpha_i) = \sum^n_{i=1} \alpha_i - \frac{1}{2} \sum^n _{i=1} \sum^n_{j=1}\alpha_i\alpha_j y_iy_jx_i^Tx_j\]이때 SVM의 한계 중 하나는 결국 경계’선’을 그어야 한다는 것인데, 선을 어떻게 그어도 완벽한 분류가 불가능한 데이터를 만났을 때입니다.
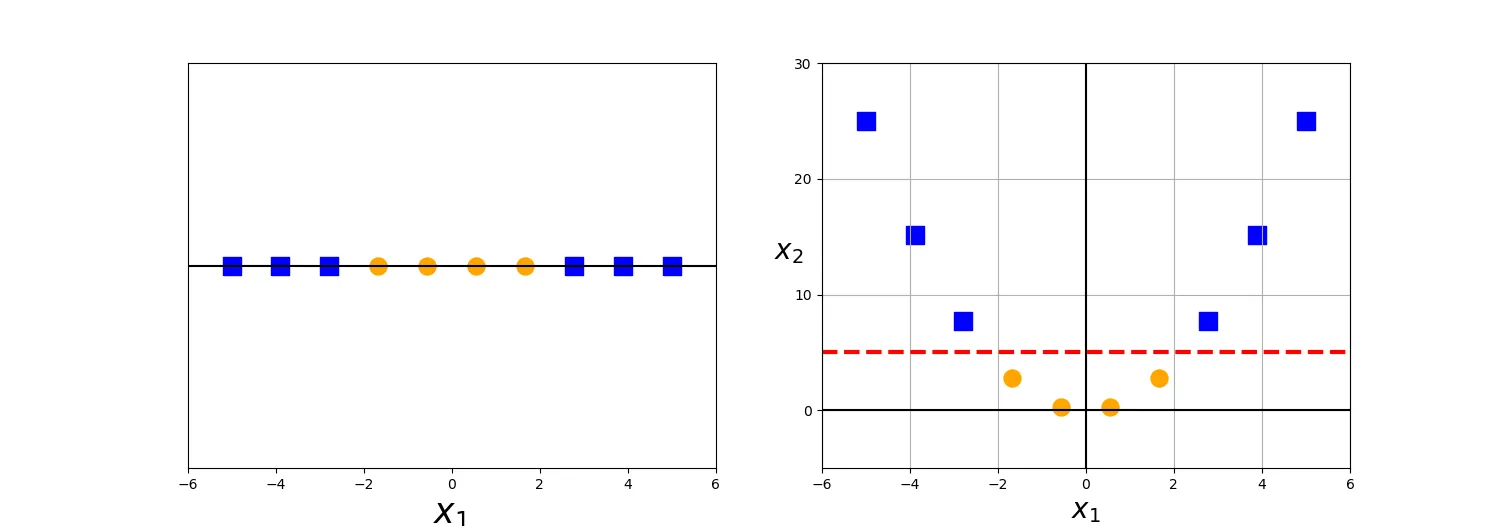_이미지 출처__
이 그림이 바로 그런 예시인데요, 좌측처럼 1차원인 상태에서는 하나의 선으로 두 개의 그룹을 분류할 수 없었지만, 이를 2차원으로 변환하자 최적의 선을 찾을 수 있는 게 보입니다. 만약 이처럼 매번 어떤 맵핑 함수 $\Phi$ 가 있어서, 우리가 가진 원래 데이터를 선을 그어서 분류가 가능한 새로운 데이터로 바꿔줄 수 있다면 어떨까요? 원래의 목적 함수는 다음과 같이 변환됩니다.
\[\max L_D(\alpha_i) = \sum^n_{i=1} \alpha_i - \frac{1}{2} \sum^n _{i=1} \sum^n_{j=1}\alpha_i\alpha_j y_iy_j \Phi(x_i)^T\Phi(x_j)\]문제는 이러한 맵핑으로 원 데이터를 고차원으로 변환하는 것, 그리고 그것을 내적하는 것 ($\Phi(x_i)^T\Phi(x_j)$ )에 상당한 연산 비용이 든다는 것입니다.
또 여기서 해결책으로 커널이 등장합니다. 여기서 커널 함수 K는 다음과 같이 정의됩니다.
\[K(x_i, x_j) = \Phi(x_i)^T\Phi(x_j)\]머서의 정리에 따르면, 커널 함수 $K$가 특정 조건을 만족하기만 하면 $K(x_i, x_j) = \Phi(x_i)^T\Phi(x_j)$ 인 맵핑 함수 $\Phi$ 가 존재한다고 합니다. 따라서 우리가 $K$를 이용한다면 $\Phi$를 실제로 찾을 필요도 없고 무엇보다 매우 비용이 큰 내적 계산을 건너뛸 수 있습니다! 이걸 바로 커널 트릭이라고 합니다.
또 재미있는 점은, $K$는 두 개의 서로 다른 벡터의 내적이므로 수식상으로 코사인 유사도를 계산하는 것과 아주 비슷하게 생겼습니다. 즉 KDE에서와 마찬가지로 이 함수는 일종의 유사도 함수로 볼 수 있는 것이죠. 특히 커널이 될 수 있는 조건 중 하나가 대칭성, 그리고 positive-definite한 성질이 있는 점도 이런 해석과 어긋나지 않습니다.
커널 SVM에서 커널이란 선형 분류가 가능하도록 데이터를 변환할 때 고차원 맵핑 및 내적에 필요한 연산량을 감소시키기 위한 기교로서 사용되는 함수
마무리
커널이란 특정 조건을 만족하는 함수이고, 어떤 목적으로 사용하느냐에 따라서 커널이 뭐냐는 질문에 따라 다른 답을 할 수 있겠지만, 일반적으로 만족하는 특성 상 어느 정도는 그 사용 방식에서 지속되는 공통점이 있는 것 같습니다(smoothing 목적으로 쓰인다거나, 가까움의 표현 유사도로서 해석될 수 있다거나). 저는 커널이 사용되는 하나의 방식을 이해하는 게 다른 방식을 이해하는 데도 도움이 된다고 느꼈는데, 부디 읽는 분들에게도 비슷하게 도움이 되기를 바랍니다.