Isolation Forest 로 이상치 찾기 (+ SHAP로 설명하기)
설명 가능한 이상치 탐지를 위해 Isolation Forest 모델을 적용하고, 그 결과를 SHAP으로 설명하는 방법을 알아봅니다. 각 방식의 개념과 간단한 파이썬 코드를 포함하고 있습니다.
오늘도 이상치 탐지(Anomaly detection) 이야기로 돌아왔습니다.
보통 이상치를 찾을 때 단변량(변수가 하나밖에 없는) 상황이라면 간단하게 z-score, IQR 등으로 분포에서 멀리 떨어진 관측치를 찾아 볼 수 있습니다. 만약 변수가 매우 많은 다차원의 데이터를 가지고 있다면? 유사한 접근으로 마할라노비스 거리와 같은 방식을 사용해볼 수도 있겠고, 그 외에도 다양한 방식이 가능할 텐데요. 오늘은 그 중 간편하게 적용해볼 수 있는 트리 기반 방법을 소개해보려고 합니다. 그리고 SHAP이 제공하는 플랏들을 사용해서 그 이상치 탐지의 결과를 설명해보는 것까지 같이 해보겠습니다.
Isolation Forest 🌳
아이디어
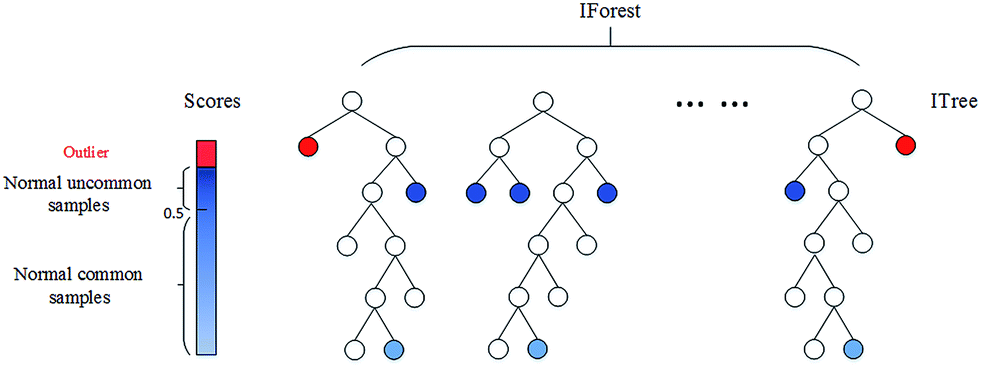
동어반복 같지만 Isoation Forest는 Forest입니다. 포레스트라는 것은, 널리 알려진 랜덤 포레스트처럼 여러 개의 의사결정나무(Decision Tree)가 모여 있는 앙상블 모델이라는 뜻입니다. 일반적으로 랜덤 포레스트 내에서 각자의 의사결정나무는 정해진 라벨에 대해 주어진 데이터를 가지고 최적의 결정 경계를 학습하는 방식으로 작동을 하는데요, Isolation Forest 속의 의사결정나무 iTree(*논문에서는 이 모델을 간단히 iForest, 각 나무를 iTree라고 부릅니다.)는 각 관측치를 따로따로 고립시키는 것을 목적으로 훈련됩니다. 이때 라벨은 필요하지 않기 때문에 이 모델은 비지도학습 방식입니다.
고립(isolate)시키는 것은 말 그대로 특정 개체를 나머지 개체로부터 완전히 구분짓는 것을 의미합니다. 이 모델이 이상치 탐지 목적으로 사용될 수 있는 핵심 아이디어는, 정상적인 관측치라면 고립시키기 어려울 것이고 이상한 관측치라면 고립시키기 쉬울 것이다! 라는 가정입니다.
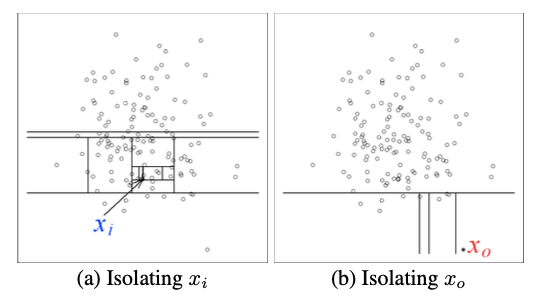
이 그림을 보면 조금 더 이해하기 쉽겠습니다. 좌측(a)처럼 다른 관측치들 한가운데에 위치한 정상치는, 오로지 이 값만 속하는 외딴 구역을 만들기 위해서 굉장히 여러 번의 경계짓기(split)가 필요합니다. 반면 우측(b)처럼 홀로 떨어진 이상치는 비교적 적은 수의 split만 해도 쉽게 고립시킬 수 있습니다.
예를 들어 전체 학생이 300명이 있고, 반/키/사는 곳/취미/성적 등등 다양한 정보가 있는데, 그 300명 중 키가 190cm가 넘는 학생이 단 1명밖에 없다면 그 학생을 분리시키는 데에는 키≥190cm 이 조건 하나만 있으면 되겠죠. 반면 다른 많은 특성이 나머지 학생들과 비슷한 친구가 있다면, 우리는 그보다 더 많은 조건을 나열해야 그게 누구인지 특정할 수 있을 것입니다. “3반에 왜 그 누구냐 키 중간 정도고…성적도 중간 정도고…축구 좋아하고… 학교 앞에 대형 아파트단지 살고…” (=누군지 전혀 모르겠음)
작동 방식
전반적인 구조는 랜덤 포레스트와 비슷합니다. 랜덤 포레스트가 랜덤하게 선택한 피쳐로 여러 개의 의사결정나무를 훈련시켜서 그 결과를 앙상블하는 것처럼, iForest는 샘플링한 데이터를 가지고 랜덤한 피쳐로 훈련되는 iTree의 결과를 합친 것입니다.
그러면 (랜덤 포레스트의 트리와 달리) 각각의 iTree는 무엇을 할까요? 위에서 언급했듯 iTree의 목표는 모든 관측치를 외딴 섬으로 분리시키는 것입니다. 다만 비지도학습이기 때문에 우리가 미리 가지고 있는 이상치에 대한 정보나 특징 같은 건 없습니다. 그래서 각각의 iTree는 샘플링한 데이터를 가지고 랜덤한 변수에 대해 랜덤한 split을 반복합니다. 매번 고른 변수의 최소값과 최대값 사이에서 uniform한 학률로 split point를 고르는데, 이것을 모든 관측치가 고립될 때까지 또는 정해진 횟수만큼 반복하는 것입니다. 그리고 이때 각 관측치가 고립되기까지의 경로 길이(루트 노드로부터 최종 고립시키는 split까지의 depth)를 매번 저장해 둡니다.
랜덤 split을 반복하는 것이 너무 아무렇게나 하는 거 아닌가? 싶어도, 이 짓을 여러 번 한다면(=앙상블한다면) 결국 이상치는 비교적 쉽게 분리되게 되어 있으며, 일정 이상 반복할 경우 robust한 결과를 내게 되어 있다는 점이 이 모델의 핵심입니다.
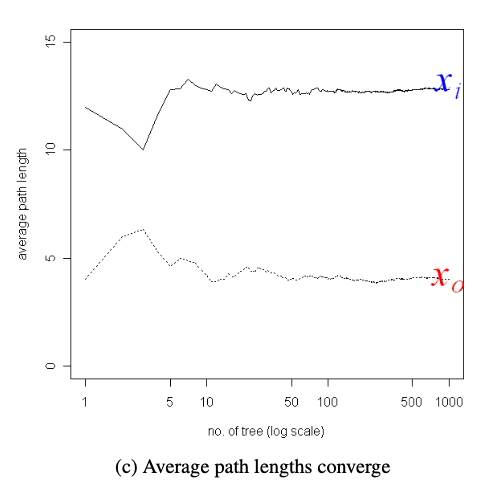
위 그림은 이 모델이 iTree가 아닌 iForest여야 하는 이유를 보여 줍니다. tree의 개수가 늘어날수록 정상치든 이상치든 각각의 경로 길이의 평균이 일정한 값으로 수렴하는 걸 볼 수 있죠. 즉 나무를 많이 쓰면 쓸수록 각 데이터 포인트의 평균 경로 길이가 안정적이게 됩니다. 논문의 결과에서는 50~100개 정도의 구간에서 값이 안정화되는 것으로 나오네요.
점수 산출
그래서 우리가 궁금한 것은 결론적으로 각 관측치가 이상치냐 아니냐입니다. iForest는 이 질문에 대한 답을 앞서 언급한 경로 길이를 가지고 계산한 0부터 1사이의 점수로 나타냅니다. 이 점수가 바로 각 관측치가 ‘얼마나 이상한지’를 나타내는 값이 됩니다.
공식은 이렇습니다.
\[s(x,n) = 2^{-\frac{E(h(x))}{c(n)}}\]- $E(h(x))$ : 각 관측치 $x$의 각 iTree에서 경로 길이가 $h(x)$라고 하면, 이 값은 전체 iTree에 대해 경로 길이를 평균낸 값
- $c(n)$ : 위 값을 정규화하기 위한 값으로, 각 나무가 사용한 훈련 데이터 개수 $n$에 대해
- $2H(n-1) - \frac{2(n-1)}{n}$
- $H(i) = ln(i) + 0.5772$
- $2H(n-1) - \frac{2(n-1)}{n}$
케이스를 나눠서 살펴보면요,
- 정상이다 = 평균 경로 길이가 평균과 비슷하다 → score 값은 1/2=0.5에 가까워짐
- 이상이다 = 평균 경로 길이가 짧다 → score 값은 1에 가까워짐
즉 점수가 커질수록 이상치에 가깝고, 0.5 정도까지는 정상에 가깝다고 볼 수 있겠습니다.
장점
iForest가 지니는 장점은 다음과 같습니다.
- 계산량이 적고 속도가 빠르다.
- 특히 다른 많은 이상치 탐지 방식은 데이터의 밀도나 거리를 계산하는 방식으로 접근하는데, 그러면 계산 비용이 높아질 수밖에 없다.
- 이상치 여부 1 또는 0만이 아니라 이상치 점수를 산출해주기 때문에 사용자가 원하는 cut-off 값을 적용할 수 있다.
- 예를 들면 저 점수가 높은 순서대로 정렬해서 직접 데이터를 보면서 어 이 정도면 이상하다고 보고 빼고 싶어/찾고 싶어!(*목적에 따라 마음대로)를 정할 수 있다.
- 학습 데이터에 꼭 이상치가 포함되어 있지 않아도 잘 작동한다.
써보자!
1
2
3
4
5
6
from sklearn.ensemble import IsolationForest
from sklearn.datasets import load_wine()
import pandas as pd
d = load_wine()
df = pd.DataFrame(data = d.data, columns=d.feature_names)
당연히 IForest를 불러와주고요, 오늘은 와인 데이터를 사용해보겠습니다. 13개의 피쳐를 사용하여 와인 등급 분류를 목적으로 하는 데이터인데 지금은 타겟값은 필요가 없을 것 같습니다. 여느 싸이킷런 모델처럼 간단하게 다음과 같이 fit 메서드를 이용해 써볼 수 있습니다.
1
2
3
4
5
6
7
8
9
iForest = IsolationForest(n_estimators = 100,
contamination = 0.01,
#contamination = 'auto',
max_samples = 30,
bootstrap = False,
max_features = 5,
random_state = 42
)
iForest.fit(df)
파라미터
c_estimators: 나무의 개수(디폴트 100)contamination: 전체 데이터에서 (예상되는/지정된) 이상치 비율.- 사실상 이 값이 이상치 점수의 threshold를 정하는 역할을 한다(점수에 영향을 주는 건 아니고). 내가 이상치는 1%라고 정했는데 점수의 상위 1% 선의 값이 0.75라면 0.75 이상을 이상치로 판단하게 되는 것.
auto설정도 있는데(그냥 무조건 0.5로 자르는), 개인적으로는 이렇게 한 다음 최종 데이터를 살펴보고 threshold를 정하는 방식을 더 자주 사용했다. 모델을 돌리기 전에 이상치가 얼마나 있을지 알기는 쉽지 않기 때문.
max_samples: 각 나무 훈련 시 샘플링하는 개수이며 디폴트 256개.- 0~1 사이의 실수로 지정하여 전체 데이터 개수의 비율을 지정할 수도 있다.
bootstrap: 각 나무 훈련을 위한 샘플링 시 True이면 복원추출, False이면 비복원추출.max_features: 각 나무 훈련 시 랜덤 선택하는 피쳐의 개수. 디폴트는 1개씩.- 마찬가지로 0~1 사이의 실수로 지정하여 전체 피쳐 중 비율을 지정할 수 있다
결과로 다음과 같이 predict와 score_samples 메서드를 사용해서 이상치 점수와 contamination 조정에 따른 이상치 라벨을 받을 수 있습니다.
- 이상치 라벨: 이상치이면 -1, 정상이면 1
- 이상치 점수: 점수를 음수로 바꿔서 보여준다는 점에 유의. 즉 높을수록(1에 가까울수록) 이상치인 이상치 점수를 반대로 바꿔놨기 때문에, 더 작은 수일수록 이상치이다. (0.7 → -0.7)
1
2
3
4
5
6
y_pred = iForest.predict(df)
y_score = iForest.score_samples(df)
df['anomaly_label']= y_pred
df['anomaly_score'] = y_score
df[df['anomaly_label']==-1].head(5)
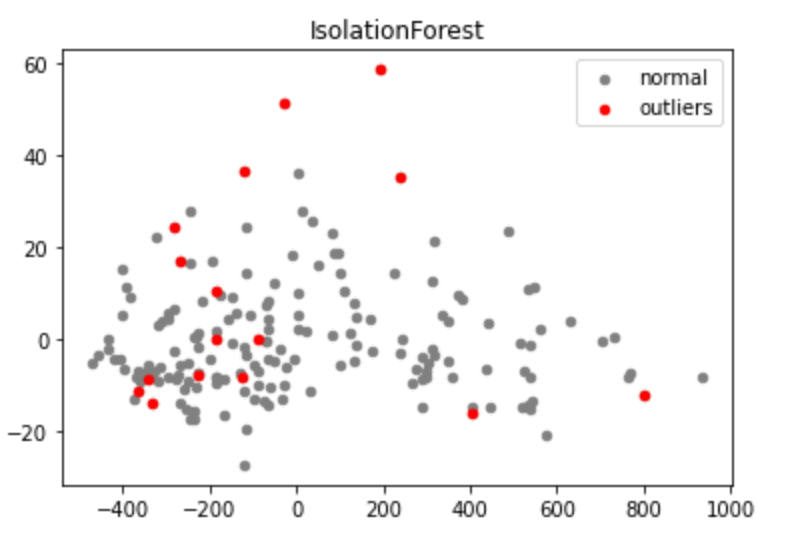
2차원으로 축소한 후 그림을 그려 봅시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
outliers = df.loc[df.anomaly_label==-1]
outlier_index = list(outliers.index)
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
pca = PCA(2)
pca.fit(df)
res = pd.DataFrame(pca.transform(df))
plt.title("IsolationForest")
b1 = plt.scatter(res[0], res[1], c='gray', s=20, label="normal")
b1 = plt.scatter(res.iloc[outlier_index,0],res.iloc[outlier_index,1], c='red',s=20, edgecolor="red",label="outliers")
plt.legend(loc="upper right")
plt.show()
설명을 어떻게 하지?
만약 이걸 사용하는 사람의 목적이 분석 결과에 영향을 줄 만한 이상치를 제외하고 싶은 거면 여기서 그냥 멈춰도 됩니다. 대충 이상치 점수 높은 데이터는 제외하고 그다음에 진짜 하고 싶은 걸 하면 되겠죠(아마도요?). 하지만 이상치를 찾아서 그 다음에 뭔가를 하고 싶은 거라면, 아니면 단순히 빼는 데에도 뭔가 설득과 의사결정이 필요하다면, 그때는 이상이냐 아니냐를 보는 것만큼이나 설명이 중요해지겠습니다.
여기서 설명이란 다음 질문에 대답하는 것입니다.
걔가 왜/어떻게 이상한데?
제가 도입부에 들었던 예시라면, 걔는 키가 195cm라서 이상하다고 대답하면 되겠죠. 수많은 변수 중 그 친구를 가장 쉽게 구분짓는 건 키라고, 보통 걔만큼 키가 크지 않다고 말입니다.
하지만 많은 경우 다차원의 데이터셋을 가지고 특정한 이상치에 대해서 그렇게 정확하고 명쾌한 대답을 하는 건 쉽지가 않습니다. 저 위의 예제에서도 제가 2차원으로 축소한 다음에 플랏을 그렸는데요. 저 빨간 점의 데이터들 중 하나를 집어서 물어본다면, 그 관측치가 정확히 뭐가 어떻게 이상한지를 말할 수 있을까요? 당연히 못합니다. PCA 자체가 13개를 2개로 줄여서 데이터의 특성을 표현을 할 수는 있는데, 원래 변수랑 엄밀히 맵핑은 안 되죠. 하지만 우리가 의사결정에 직관적으로 사용할 수 있는 건 원래 변수고요.
그러니까 많은 머신러닝 모델들처럼, 이번에도 우리는 이게 이상한데 왜 이상한지는 잘 모르겠어 (혹은 간단히 말하긴 좀 그래) 라는 상황에 봉착하게 된 것입니다.
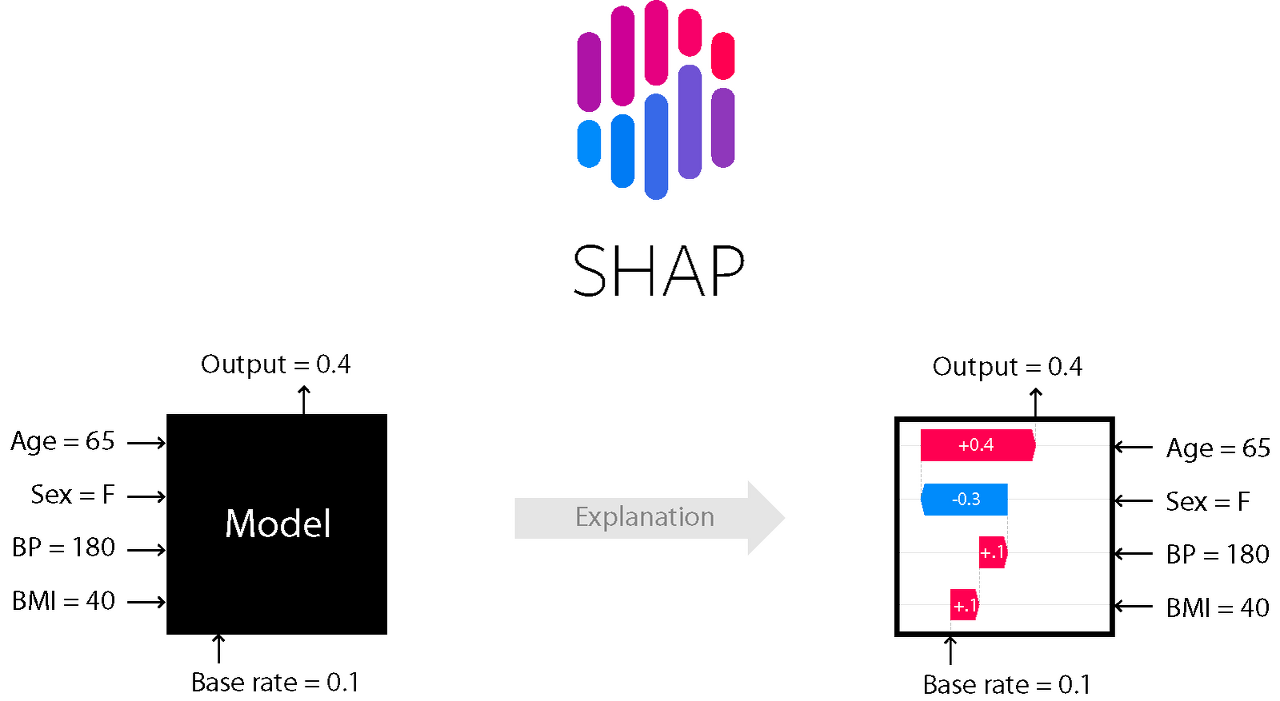
SHAP (SHapley Additive exPlanation)
Shapley Value는 게임이론을 기반으로 게임 내 각 참가자가 기여한 정도를 계산해서 지불금을 주자는 개념에서 출발했습니다(*Shapley라는 사람이 처음 언급했다고 합니다). 이것을 설명 가능한 AI(XAI; eXplainable AI)의 관점에서 풀어 쓰자면, 각 관측치에 대한 모델의 예측(=게임)을 가지고 각 피쳐(=참가자)가 그 예측에 대해 기여한 정도를 보자는 것입니다. 이를 위해서 Shapley Value는 모든 가능한 피쳐의 부분집합을 만들어서 각 피쳐가 있을 때와 없을 때의 차이를 기여분으로 계산하고 이를 가중평균합니다. 다만 이를 계산하기 위해서는 계산 비용이 매우 크므로, SHAP은 이런 Shapley Value의 근사값을 구하는 여러 가지 방식을 제공해 줍니다(Tree/Kernel/Deep SHAP 등).
결과 위주로 간단히 말하면 SHAP은 예측에 대한 각 피쳐의 영향력을 방향과 크기로 표현해주는 방법이라고 할 수 있겠는데요. 오늘은 해당 방법 자체를 상세히 보는 것보다는 이것을 사용해 Isolation Forest의 결과를 설명하는 데 중점을 두고 적어보겠습니다. SHAP에 대한 자세한 설명은 여기를 참고하실 수 있습니다.
iForest + SHAP
SHAP은 여러 가지 종류의 Explainer를 제공하는데, 신경망이나 트리 모델에 특화된 Explainer가 있는 반면, 어떤 종류의 모델에도 적용할 수 있는 Explainer가 있는데요(KernelExplainer와 Explainer). 오늘은 TreeExplainer를 사용해보도록 하겠습니다. 인풋으로 아까 훈련한 Isoation Forest 모델과 원 데이터를 넣어주고, 다음과 같이 SHAP 값들을 계산해 줍니다.
1
2
3
import shap
explainer = shap.TreeExplainer(model = iForest, data = df)
shap_values = explainer.shap_values(df)
각 관측치에 대한 설명
SHAP이 제공하는 가장 즉각적인 설명은, 관측치 하나하나에 대해 모델이 그런 (이상치이다/아니다) 예측을 내리는 데 어떤 피쳐가 가장 크게 기여했는지를 보여줄 수 있다는 점입니다.
우선 이상치 중 하나의 인덱스를 골라서 shap_values를 확인해보면, 피쳐 개수와 동일한 13개의 값이 들어있는 array를 확인할 수 있습니다.
1
print(shap_values[69])
이 값들이 바로 모델의 아웃풋에 대한 각 피쳐의 기여도와 기여 방향을 의미하는데요. 이걸 그림으로 보면 조금 더 편합니다.
1
shap.force_plot(explainer.expected_value, shap_values[110],feature_names = d.feature_names)
- 여기서 base value는 약 11.1로, 이는 전체 예측값의 평균이다. 반면 이 관측치의 예측값은 8.35이다.
- 어? 뭔가 이상한 게 이 모델의 예측값은 -1 또는 1이라며 값이 왜 이렇게 커?
- 약간의 혼란을 거쳐서 알아낸 유의사항: SHAP이 Isolation Forest의 explainer를 지원할 때, 설명하고자 하는 대상은 최종 예측 라벨(-1 또는 1)이 아니라 각 관측치의 전체 iTree 경로 길이의 평균(*이상치 점수 산출하는데 쓰는 그 값)이 되도록 구현되어있다.
- 즉 이 섀플리 값들은 이 관측치가 왜 -1(이상치)인가? 를 설명하는 것이 아니라 왜 전체 iTree 경로 길이 평균이 8.35인가(짧은가)? 를 설명한다.
- 짧을수록 score가 높고 이상치이기 때문에 결국 같은 얘기다, 하지만 처음에는 8.35가 대체 무슨 값인가 싶었다.
(참고) 해당 라이브러리 이슈 중 큰 도움이 된 코멘트
Isolation forest model_output: “decision_function” not implemented · Issue #1152 · slundberg/shap
- 다시 플랏으로 돌아가서,
- 빨간색으로 그려진 변수는 예측값을 증가시키는 데(=경로 길이 평균의 증가, 정상치로 예측) 기여한 변수들이며, 그 길이는 그 변수가 기여한 정도이다.
- 파란색으로 그려진 변수는 예측값을 감소시키는 데(=경로 길이 평균의 감소, 이상치로 예측) 기여한 변수들이며, 그 길이는 그 변수가 기여한 정도이다.
이 관측치의 경우 파란 변수들의 기여도가 훨씬 더 높았고, 빨간 변수들의 길이는 그에 비해 너무 짧아 최종적으로 낮은 예측값(-1에 더 가까운 값)을 얻었습니다. 그리고 이 관측치를 이상치로 만든 변수들 중 가장 큰 영향을 끼친 것은 마그네슘 함량임을 알 수 있습니다.
이번엔 다른 이상치 값을 봅시다.
경로 길이 평균/이상치 점수만 봤을 때는 위의 관측치와 비슷했지만, SHAP이 제공해준 변수별 기여도 값을 보면 위 관측치와 ‘다른 방식으로’ 이상하다는 것을 알 수 있습니다. 이 경우에는 마그네슘이 아닌 다른 변수(회분의 알칼리도)가 매우 높다는 것이 이 관측치를 이상치로 예측하는 데 큰 영향을 끼쳤죠.
아래는 정상 데이터로 같은 플랏을 그려본 것입니다.
이 관측치의 경우에는 빨간색(예측값을 증가시키는 데 기여한) 변수들의 기여도가 훨씬 더 크다는 것을 확인할 수 있습니다.
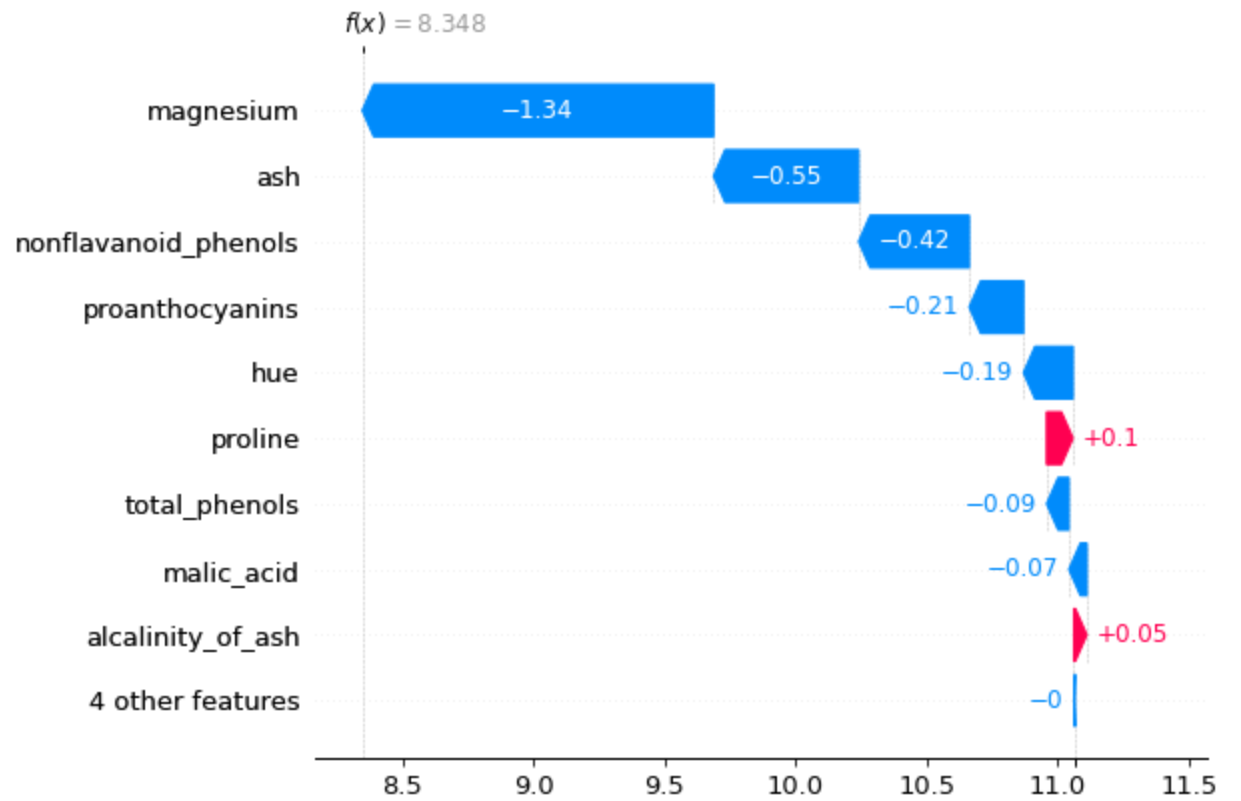
완전히 동일한 내용을 다음과 같이 Waterfall Plot으로 그릴 수도 있습니다. 이때 max_display 값을 통해 기여도가 큰 순으로 몇 개까지 보여줄 건지도 정할 수 있고요.
1
2
3
4
5
shap.waterfall_plot(shap.Explanation(values=shap_values[4],
base_values=explainer.expected_value,
feature_names=d.feature_names,
max_display = 8)
)
전체 피쳐에 대한 설명
SHAP은 이런 각 관측치단위 설명 외에도 굉장히 다양한 관점의 설명을 제공합니다. 그 중 전체 데이터에 대해서 피쳐들의 전반적인 변수 기여도를 비교해볼 수 있는 플랏도 있습니다.
1
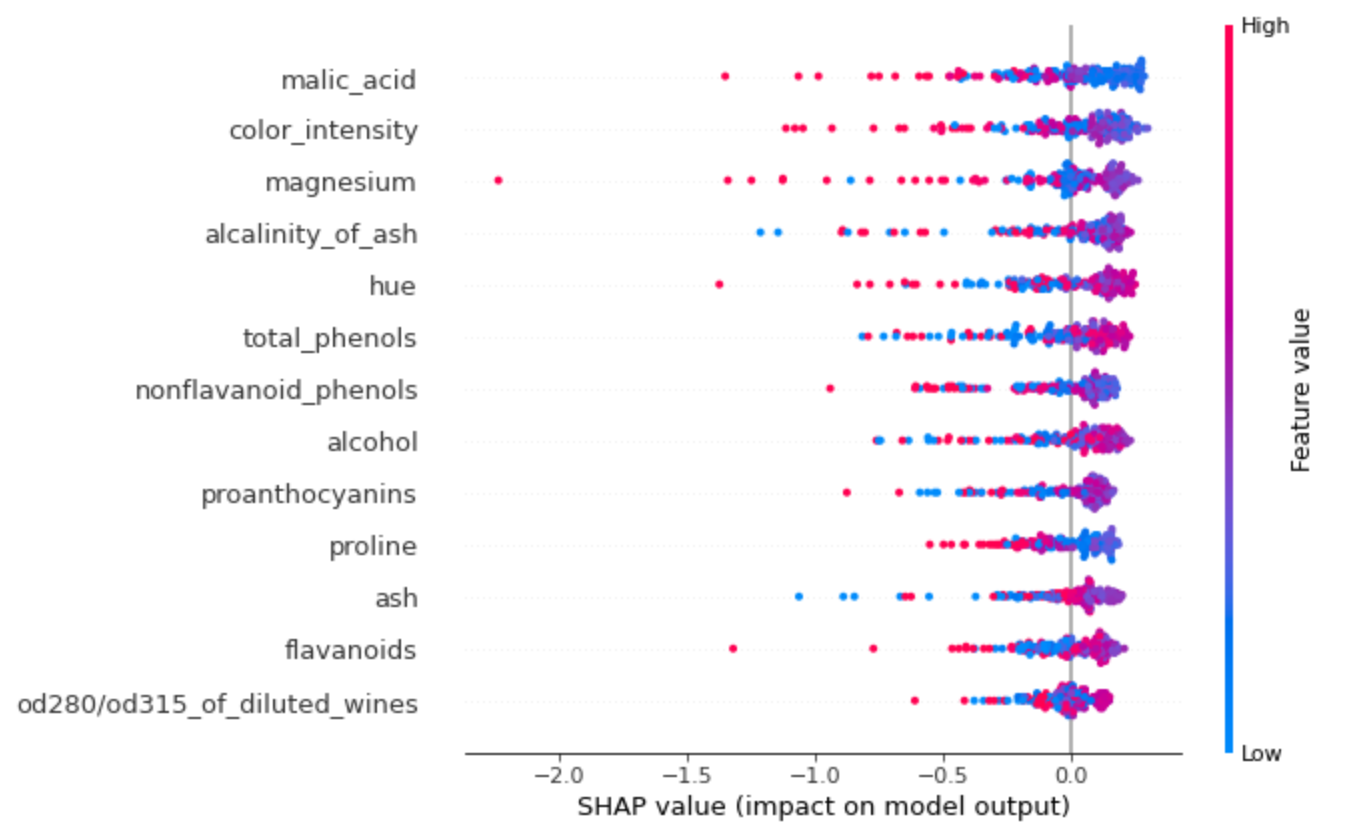
shap.summary_plot(shap_values, df)
- 이 플랏은 우선 각 피쳐마다 섀플리 값의 절대값(즉 증가/감소 방향 고려하지 않고)을 합하여 큰 순서대로 정렬한 것이다. 즉 가장 위에 있는 말산이라는 피쳐가 전반적으로 봤을 때 피쳐 기여도가 가장 높다.
- 이 플랏에서 빨간색/파란색의 값이 의미하는 바는 그 피쳐의 값이 큰지 작은지인데, 섀플리 값이 음의 방향으로 높은(즉 이상치에 대한 기여도가 큰) 관측치들이 어떤 색인지를 보면 그 피쳐의 크고 작음이 전반적으로 이상치에 영향을 주는지를 알 수 있다.
- 뭔 소린지 모르겠으니까 풀어서 쓰면, 예를 들어 1위인 말산 같은 경우는 음수 섀플리 값이 큰 점들을 보면 대부분 빨간색이다. 즉 말산 값이 큰 관측치들이 이상치로 예측이 많이 되었다.
- 반면 밑에서 3번째인 회분 같은 경우는 음수 섀플리 값이 큰 점들이 파란 색인 경우가 많다. 즉 회분 값이 낮은 관측치들이 이상치로 예측되는 경향이 있다.
- 이걸 좀 더 자세히 보고 싶으면 다음과 같이 각 피쳐마다 Dependence Plot을 그려본다.
1
2
shap.dependence_plot(1, shap_values, df)
shap.dependence_plot(2, shap_values, df)
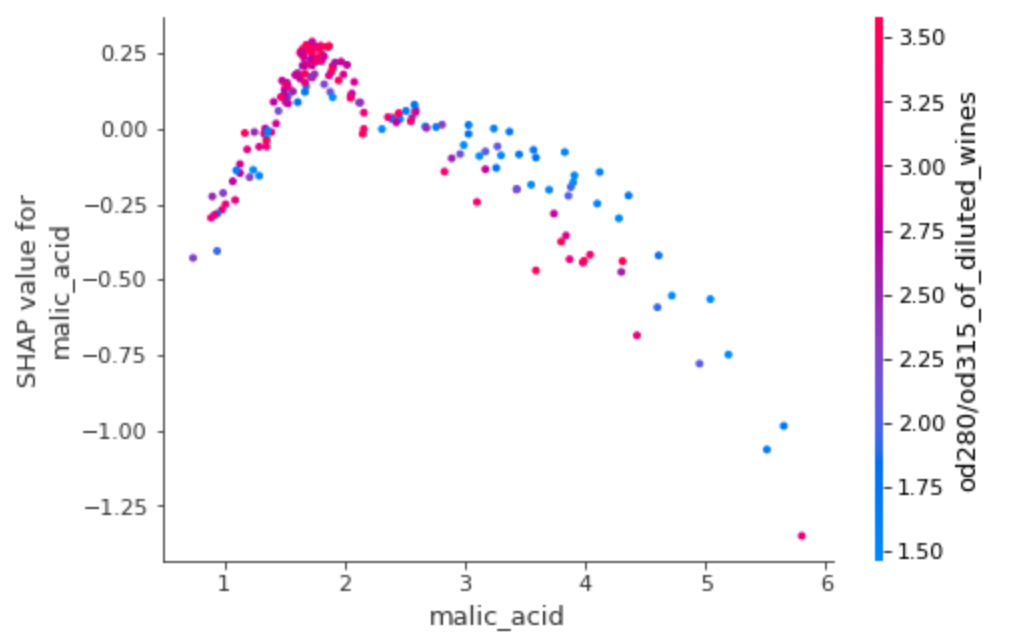말산 - 갚이 커질수록 섀플리값이 음수 방향으로 절대값이 커진다
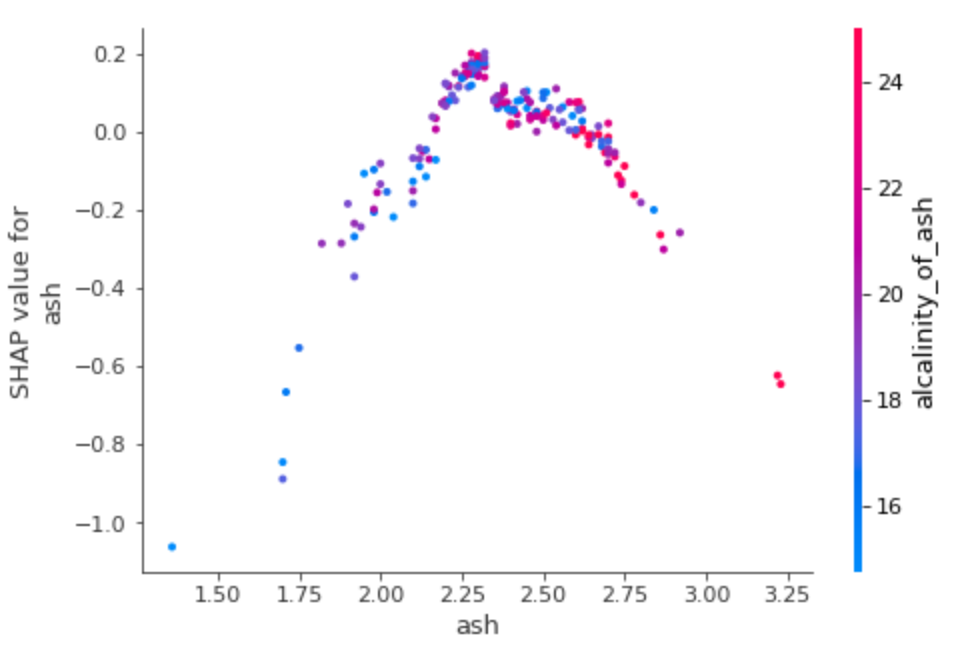회분 - 값이 작아질수록 섀플리값이 음수 방향으로 절대값이 커진다
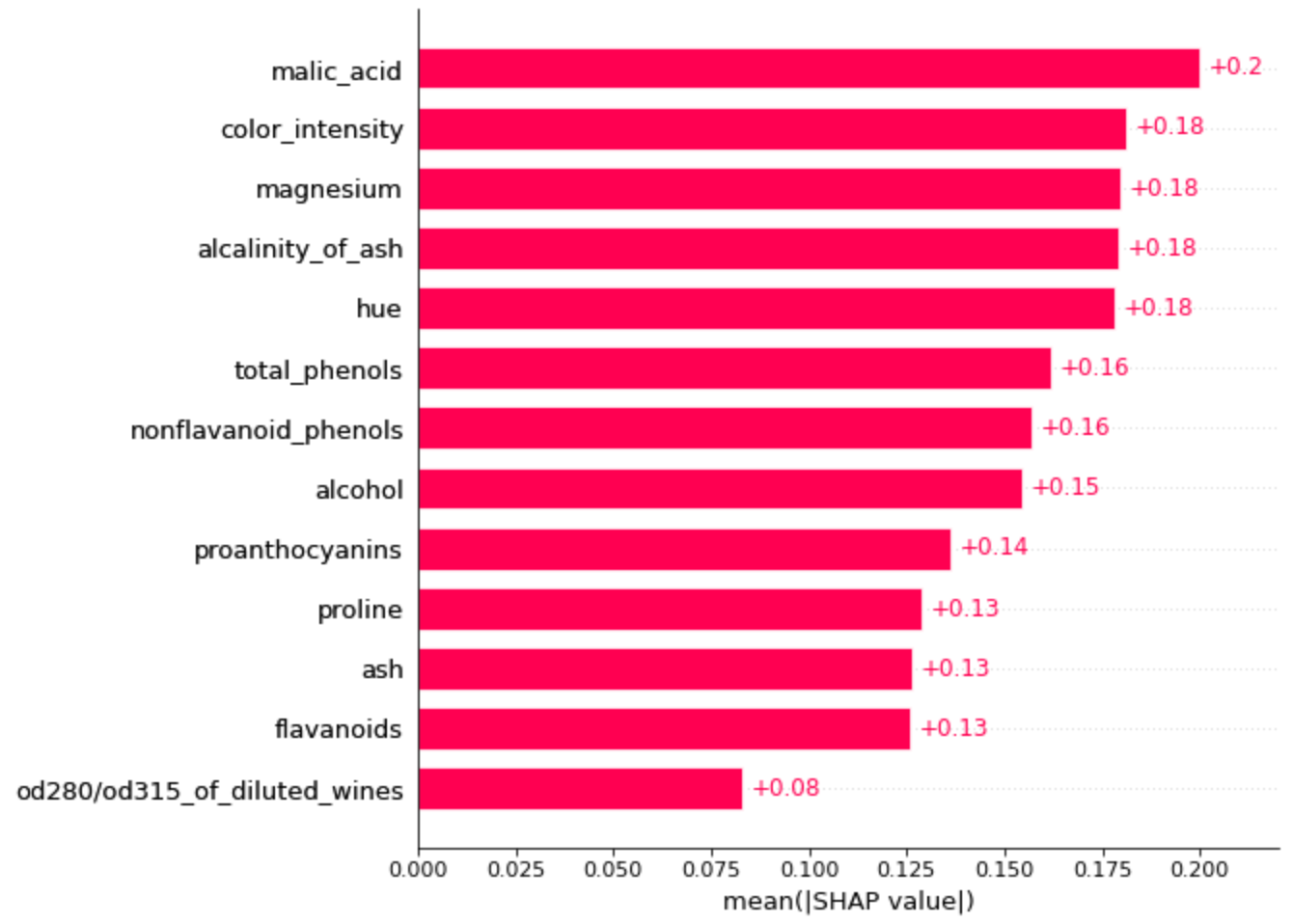
이런 경향성 말고 그냥 전반적인 피쳐 기여도(중요도)만 간단하게 보고 싶으면, 아래와 같이 섀플리 값 절대값이 평균을 바 플랏으로 그려 봐도 됩니다.
1
shap.plots.bar(shap.Explanation(shap_values,feature_names=d.feature_names), max_display=14)
