라벨이 불균형하면 오버샘플링을 하라던데
그런데 다들 말하는 것만큼 효과가 있는 게 맞을까요? Is Augmentation Effective in Improving Prediction in Imbalanced Datasets? (2024) 를 읽어보았습니다.
분류 문제에서 모델이 예측하고자 하는 타겟 Y의 분포는 현실 세계에서는 대부분 불균형하기 마련입니다. 즉 어떤 라벨의 데이터 수가 다른 라벨보다 많거나 적을 가능성이 큽니다. 예를 들어 MNIST 같은 데이터에서는 라벨이 1이 100개, 2가 100개, 3이 100개, 이렇게 두고 연습할 수 있겠지만 실제 마주하게 되는 데이터는 보통 그렇지가 않죠. 특히 이상탐지와 같은 영역으로 가면 이상은 정상보다 훨씬 낮은 빈도로 발생하므로 심한 경우 1:10000 수준의 극심한 불균형을 만나게 될 수도 있습니다.
이러한 상황을 마주치면 대부분 각자의 도구에 검색을 하겠죠. imbalanced dataset 처리 방법 알려줘... 그러면 보통 가장 간단한 방법으로 알려주는 게 샘플링입니다. 학습할 때 데이터가 너무 많은 클래스는 덜 사용하고 데이터가 너무 적은 클래스는 어떤 방법으로든 불려서 사용하라는 건데요.
- 언더샘플링 : 더 많은 클래스(보통 majority 라고 함)를 랜덤으로 샘플링해서 일부만 사용
- 오버샘플링 : 더 적은 클래스(보통 minority 라고 함) 를 이렇게 저렇게 샘플링해서 더 많이 사용
- 이렇게 저렇게 란?
- 이미 있는 minority 데이터들을 랜덤하게 똑같이 복제해서 뽑을 수도 있고
- 이미 있는 minority 데이터들과 비슷하지만 살짝 다른 가상의 데이터를 새로 생성해서 뽑을 수도 있고
- 예를 들면 SMOTE 같은 방법들
- 이렇게 저렇게 란?
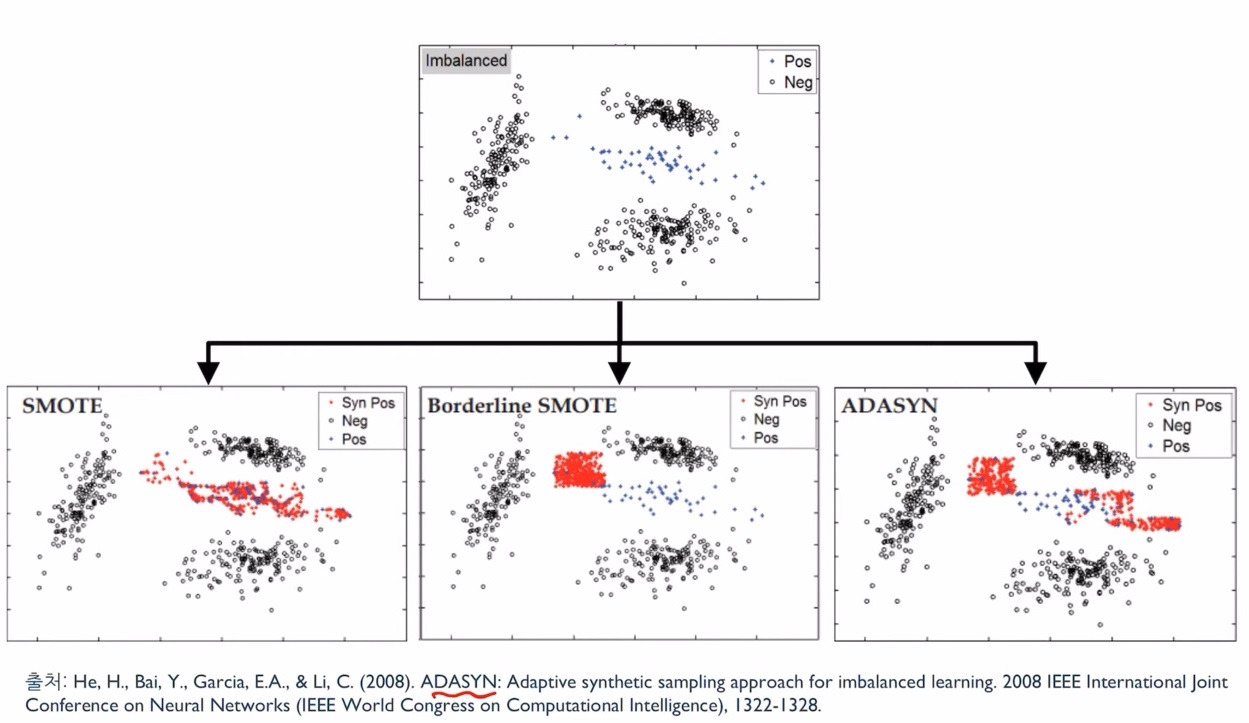
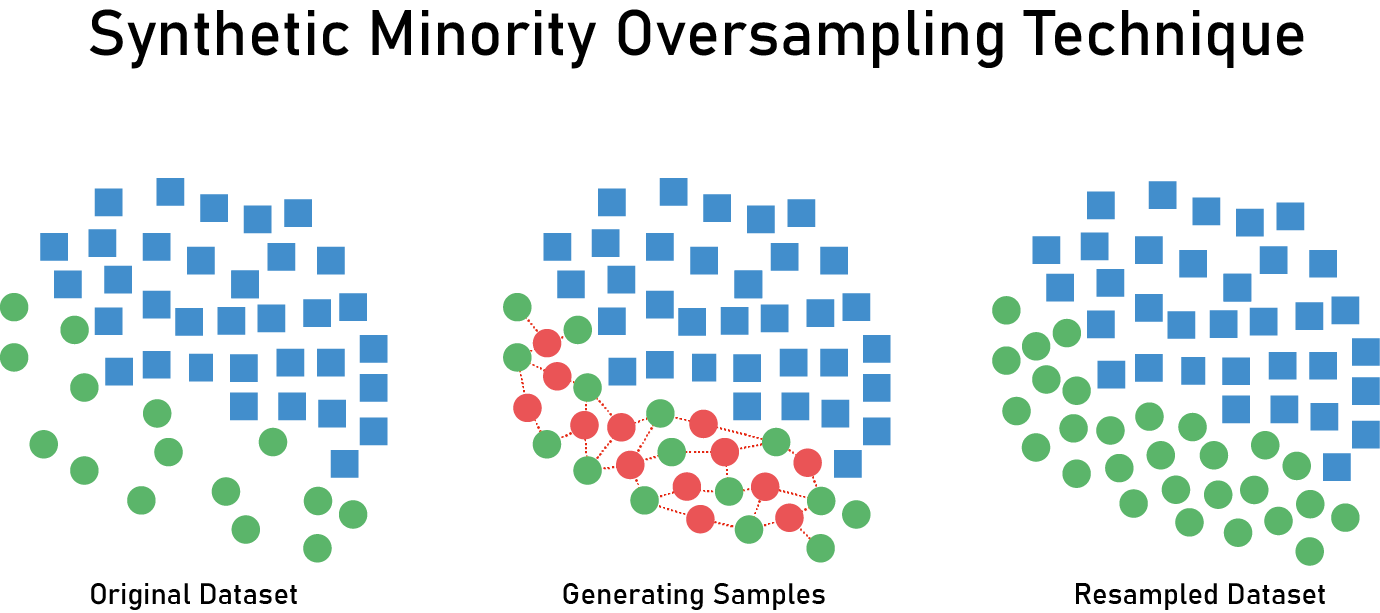SMOTE의 아이디어, 데이터를 생성해서 늘리는 방식은 대부분 아이디어는 비슷함. 그림 출처
그런데 저는 개인적으로 지금까지 캐글 데이터든 업무에서 만난 데이터든 샘플링을 해서 크게 효과를 본 적이 없습니다. 모든 건 다 상대적인 문제이므로 당연히 아무것도 안 한 것보다는 샘플링을 한 게 낫지만, 샘플링을 하는 것보다는 항상 학습 과정에서 loss에 weight을 설정하는 게 더 효과적이었습니다. 모델이 minority 클래스에 대해서 틀리는 것에 대해 더 민감하게 반응하도록 loss값을 만져주는 것인데요, 즉 1이라는 클래스가 0보다 데이터는 1/100밖에 안 되긴 하지만 1에 대해서 모델이 한번만 틀리더라도 100배 회초리질을 해주면 잘 알아먹게 된다! 라는 개념이죠. 많은 분류 모델들이 라이브러리 자체에서 이 설정을 쉽게 할 수 있도록 지원하고 있습니다. 예를 들어 sklearn의 RandomForestClassifier는 class_weight라는 파라미터가 있어서 {0:1, 1:99} 와 같은 dictionary의 형태로 특정 라벨에 얼마나 가중치를 둘지 사용자가 직접 결정하거나, balanced라는 옵션을 통해 자동으로 라벨간 비율을 계산하여 거꾸로 가중치를 맞춰주는 식으로 설정이 가능합니다.
아무튼 다시 돌아와서 제 경험 상으로는 이게 무조건 언더/오버샘플링보다 항상 성능이 좋았습니다. 그에 따라 샘플링이 정말 도움이 되는 게 맞나 하는 의구심을 가지고 있었고 특히 오버샘플링은 거의 사용하지 않고 있었지만, 그렇다고 또 샘플링의 효과를 엄밀하게 실험하거나 살펴본 적은 없었고 그냥 막연하게 오버샘플링 방식이 모델에게 전혀 새로운 정보를 주지 못하니까 성능 개선에 도움이 안 되는 거 아닐까 하고만 생각했는데요. (이런 건 딱 누가 시간과 비용 들여서 해보고 알려주면 좋은데…🍯 싶은 목록 32524개 중 하나) 이번에 마침 불균형한 데이터를 다룰 때 오버샘플링의 효과 없음에 대해서 수학적 정리와 실험으로 보여주려고 한 연구를 발견해서 소개해보도록 하겠습니다.
정리
분류 모델은 기본적으로 주어진 데이터 $x$에 대해 관심 있는 타겟 변수 $Y$가 특정 값을 가질 확률을 최대한 정확하게 추정하는 것, 즉 $P(Y=y \vert x)$를 배우는 것입니다. 참, 문제를 간단하게 생각하기 위해 모든 상황은 0 또는 1의 이진분류이며 1이 minority class라고 가정하겠습니다. 그러니까 학습된 모델이라는 것은 일단 $P(Y=y \vert x)$를 알아내고, 어떤 임계값 $c$를 정해서, $P(Y=y \vert x)$가 $c$를 넘어가면 이 샘플은 1이고 그렇지 않으면 0입니다! 라고 결론을 내는 방식으로 작동하게 됩니다. 보통 $c$의 디폴트 옵션은 0.5이고요.
이 관점에서 이 연구가 보여주려는 내용의 핵심은 이렇습니다. 원래 데이터 기준의 $P$와 데이터를 랜덤하게 오버샘플링하여 비율을 동등하게 맞춘 기준의 $P_a$가 있을 때, $P$와 $P_a$는 1:1 대응이 가능하기 때문에 $P_a$를 가지고 $c$를 0.5로 설정한 분류기나 애초에 오버샘플링을 하지 않은 $P$에 대해서 최적의 $c$를 설정한 분류기나 결국 차이가 없다는 것입니다.
우선 오버샘플링 후 학습한 모델을 $g_a(x)$ 라고 하고 이 모델이 학습한 확률을 $P_a$ 라고 합니다. 이때 일반적으로 최적의 분류기는 다음과 같고,
\[g_a(x) = \arg \min \sum L(k,j) P_a(Y=k \vert x)\]- $k$ , $j$ 는 0또는 1
- $L(k,j)$ 는 사실 $k$인 샘플을 $j$로 분류했을 때의 loss값
최적의 분류기가 되기 위한 decision rule은 다음과 같다고 알려져 있습니다.
\[g_a(x) = \begin{cases} 1 & \text{if } P_a(Y=1 \vert x) \geq \frac{L(0,1)}{L(0,1)+L(1,0)} \\ 0 & \text{otherwise} \end{cases}\]이때 $L(0,1)$과 $L(1,0)$이 동일하다면 threshold가 0.5인 것이고, 우리도 그렇다고 가정하면, 다음과 같이 $g_a(x)$는 사실 원래 데이터(오버샘플링되기 전) 기준 $P$ 로도 다음과 같이 최적의 decision rule을 만들 수가 있다는 것이 결론입니다.
\[g_a(x) = \begin{cases} 1 & \text{if } P(Y=1 \vert x) \geq P(Y=1) \\ 0 & \text{otherwise} \end{cases}\]이 글에서는 이에 대한 자세한 증명을 다루지는 않으니 증명이 궁금하신 분은 여기의 supplementary material을 다운받아 보시면 되겠습니다.
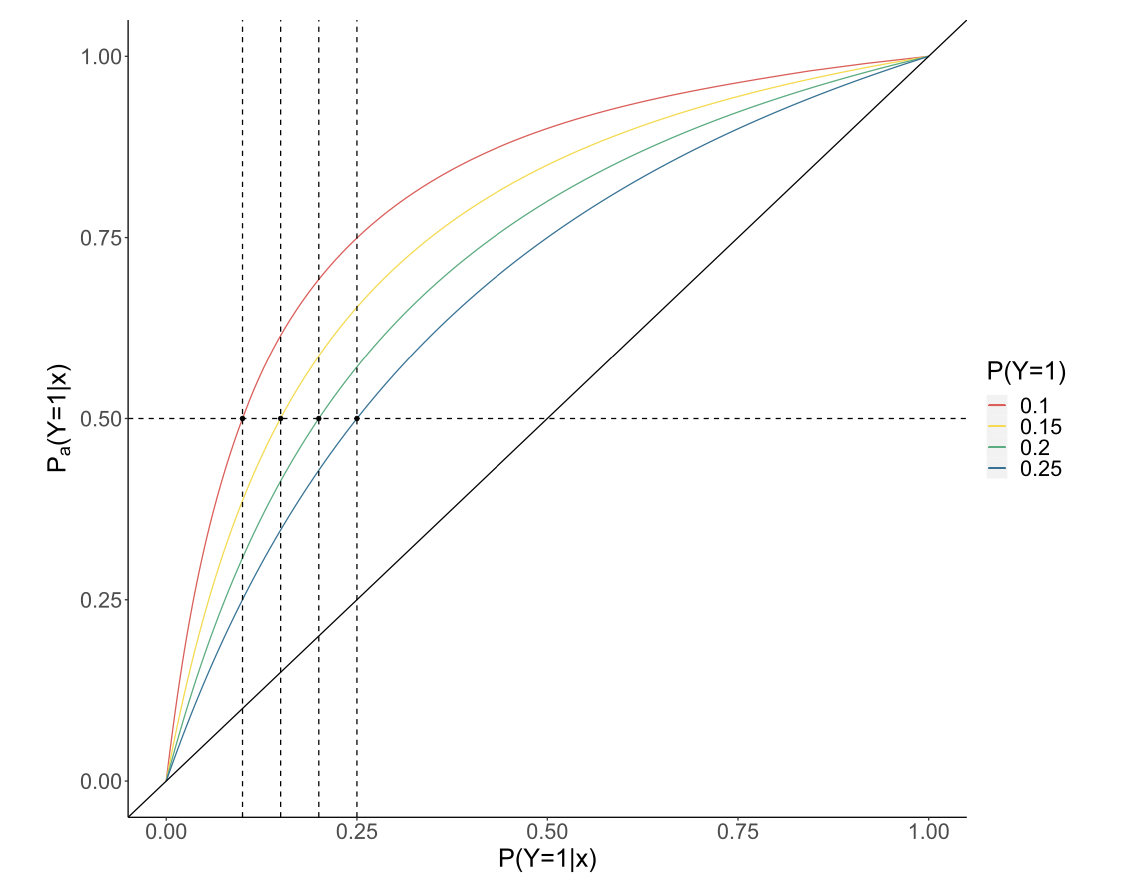
그림으로 한번 보겠습니다.
색깔 있는 선들이 바로 $P$와 $P_a$의 맵핑 관계를 알려주고 있습니다. $P(Y=1)$는 원래 데이터셋의 불균형 정도를 나타내는 것입니다. 즉 $P(Y=1)=0.1$인 경우라면, 전체 데이터 중 1이 10%밖에 안 된다는 뜻이죠. $P_a$ 에 대해 0.5라는 임계값을 정하는 것은 사실상 원본 데이터를 가지고 학습한 $P$에 대해 $c$를 $P(Y=1)$로 정한 것과 맵핑된다는 것을 보여주는 그림입니다. 왜 괜히 오버샘플링을 해서 리소스만 더 써? 그냥 애초에 decision threshold를 0.1로 하면 돼! 라는 소리인데, 1이 적을수록 더 쉽게 1로 판단(확률이 0.1만 되어도 1로 결정)하라는 것이니 직관적으로도 이상하진 않아 보이네요.
실험
수식으로는 그렇다는데 실제로도 그런지 봅시다. 게다가 이 연구는 단순 랜덤 샘플링 (복제) 뿐 아니라 SMOTE 나 ADASYN처럼 데이터를 추가로 생성하는 테크닉마저도 랜덤 샘플링과 다를 바 없는 결과를 낸다고 주장하고 있으니 이 부분도 실험으로 확인해야 할 것 같습니다.
실험은 트위터 감정 분석, 이커머스 의류 상품 리뷰, 앱 유저 리뷰, 혐오 발언, 카드 연체, 디지털 마케팅 전환여부 등 다양한 도메인에서 총 8개의 데이터를 대상으로 진행되었습니다. 데이터 크기는 적게는 8천 개부터 많게는 25만 개까지였고, 전부 라벨별 사이즈가 불균형했는데요. 예를 들어 혐오 발언 분류를 위한 데이터에서는 전체 트윗 중 7%만이 예측하고자 하는 라벨인 혐오 발언에 해당했고, 상품 리뷰에서는 18%의 리뷰만이 상품을 추천하지 않는 리뷰인 식이죠.
비교한 오버샘플링 방식은 다음 4가지였습니다.
- 랜덤 샘플링: 데이터를 새로 생성하는 것이 아닌 minority를 단순 랜덤하게 복제해서 샘플링
- SMOTE: minority 샘플들과 가까운 이웃들로 가상의 데이터를 생성
- Borderline SMOTE: 기본적으로 SMOTE이지만, 분류기가 헷갈리는 라벨간 경계에 있는 샘플들 위주로 선정하여 그 이웃들로 가상의 데이터를 생성
- ADASYN: Borderline SMOTE와 유사하지만, 경계선에 있는 샘플들마다 근처에 있는 majority 클래스 개수에 따라 샘플링 비율을 다르게 가져감
오버샘플링은 모델 성능을 개선할까?
모델 성능을 이 연구에서는 balanced accuracy로 봅니다. 다른 말로는 sensitivity와 specificity의 평균이죠. (왜냐면 사실 제가 위에 ‘알려져 있다’라고 적은 최적의 decision rule은 balanced accuracy를 최적화하는 것이기 때문..) 모델(분류기)가 $g(x)$ 이고 0 또는 1을 뱉어낸다고 할 때, 우리의 지표는 이렇습니다.
\[ba(g) = (P(g(X)=1 \vert Y=1) + P(g(X)=0 \vert Y=0))/2\]또한 관심이 있는 것은 오버샘플링 또는 data augmentation이 이 성능을 개선하는가 개선하지 못하는가이기 때문에, 오버샘플링 테크닉을 적용한 모델을 $g_a$라고 하고 적용하지 않은 기본 모델을 $g_b$라고 할 때 percentage gain 이라는 값을 다음과 같이 정의합니다. 두 버전의 모델의 성능 차이가 기본 모델의 성능 대비 얼마나 크냐, 또 음수이냐 양수이냐를 보겠다는 것입니다.
\[pg = \frac{ba(g_a)-ba(g_b)}{ba(g_b)}\]그러면 뭐랑 뭐를 비교할까요?
- $g_a$랑 $g_b$ 모두 $c=0.5$로 결정했을 때
- $g_a$는 c=0.5로 하고, $g_b$는 앞서 수식과 같이 최적의 $c$ 기준으로 결정했을 때
- $g_a$와 $g_b$ 모두 최적의 $c$로 결정했을 때
마지막 케이스의 경우 다른 테크닉들이 임계값 $c$ 조정으로는 얻을 수 없는 이득을 주는 부분이 있는지를 확인하려고 한 것입니다.
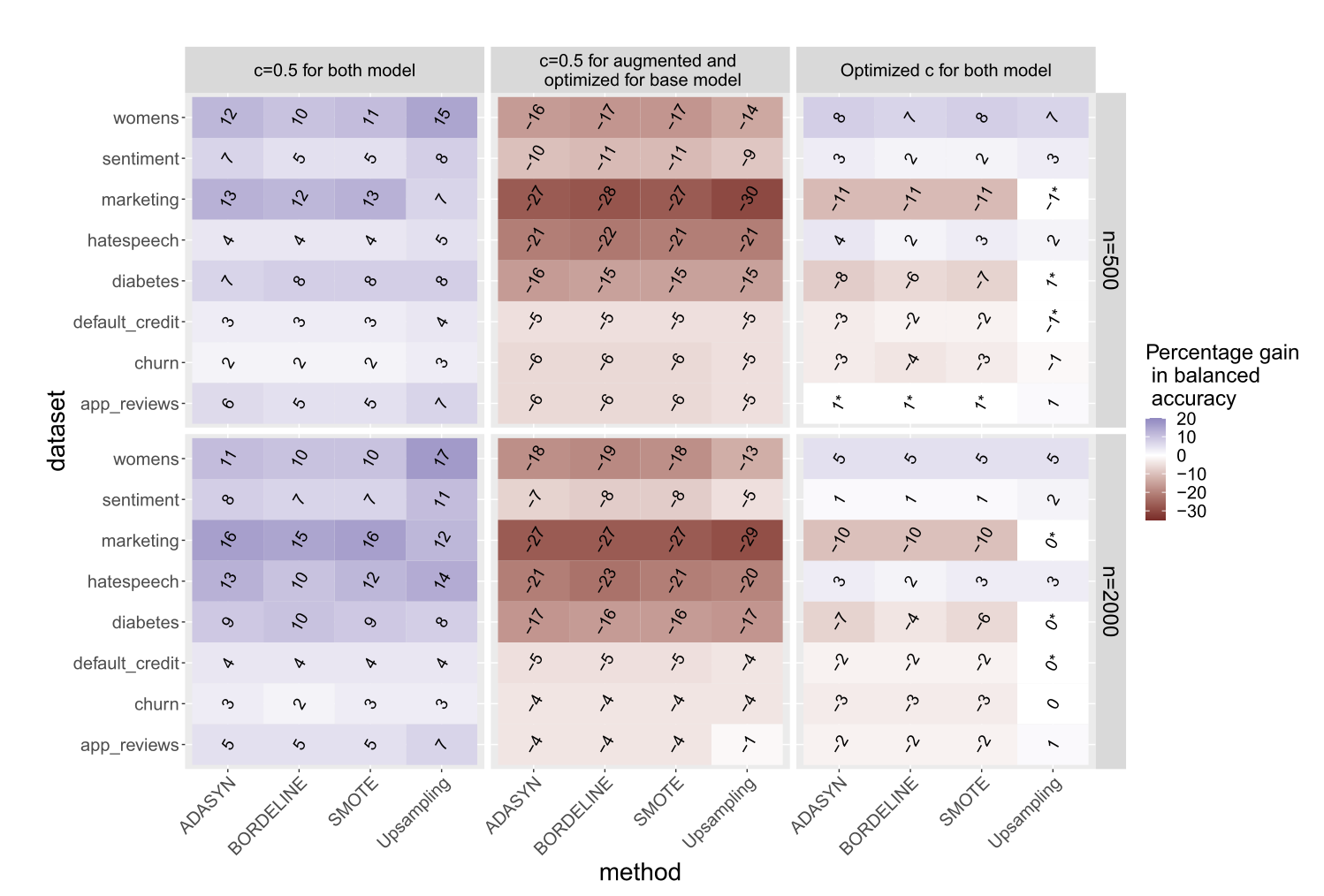
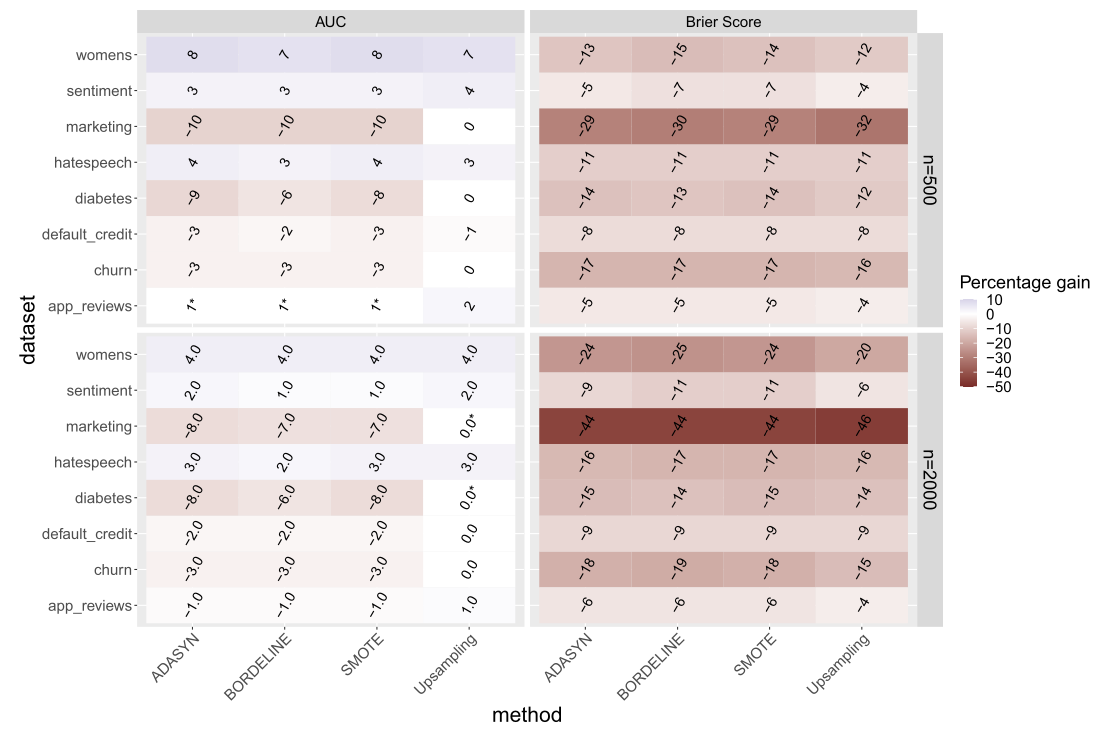
여기까지가 설정이고 다음은 결과입니다. y축이 8개의 데이터셋과 샘플링의 규모이고 x축은 위 3가지 비교 케이스와 4가지의 오버샘플링 테크닉입니다.
왼쪽부터 보면,
- 우선 둘 다 $c$를 0.5로 고정시키면(이것은 지금까지 오버샘플링이 효과 있다고 보여진 대부분의 세팅과 동일한 세팅임) 대부분의 케이스에서 오버샘플링의 percentage gain이 양수로서 즉 오버샘플링이 balanced accuracy를 상당히 증가시키고 있는 것을 확인할 수 있음
- 그러나 기본 모델에서 $c$를 최적의 $c$로 선택한 것과 비교하면 오히려 오버샘플링 테크닉들이 더 나쁜 balanced accuracy를 보여주고 있으며 랜덤 복제가 아닌 SMOTE나 ADASYN 같은 생성 방식도 동일함
- 오버샘플링 모델에서도 최적의 $c$를 선택해봤지만 별 차이가 없음 = 임계값을 고르는 것 외에 다른 모든 것이 동일하다면 오버샘플링의 업사이드는 없다고 보여짐
오버샘플링은 $P(Y=y \vert x)$ 추정을 개선할까?
마지막으로 궁금한 것은 정해진 임계값에 의존하는 balanced accuracy라는 어떤 단일 지표가 아닌, 모델이 전체적으로 $P(Y=y \vert x)$를 잘 추정했는지를 비교해보는 것입니다. 이걸 볼 수 있는 방법으로는 AUC와 Brier Score를 선택했습니다. AUC는 너무 잘 알려진 ROC curve의 면적 합이고 Brier Score 란 모델이 예측한 확률 분포와 주어진 실제 데이터 분포의 차이를 나타낸 값으로 $\mathbb{E} \lbrack (Y-\hat{P}(Y=1 \vert X))^2 \rbrack$ 라고 할 수 있습니다.
- 일반적인 표기와 반대로 통계적으로 유의하지 않은 차이에 대해서만 별($*$)을 달아놨음 (유의수준 0.01)
- AUC 면에서는 대부분 오버샘플링이 효과가 떨어지고 심지어 Brier Score 면에서는 더 나쁜 결과를 낸다는 것을 확인할 수 있음
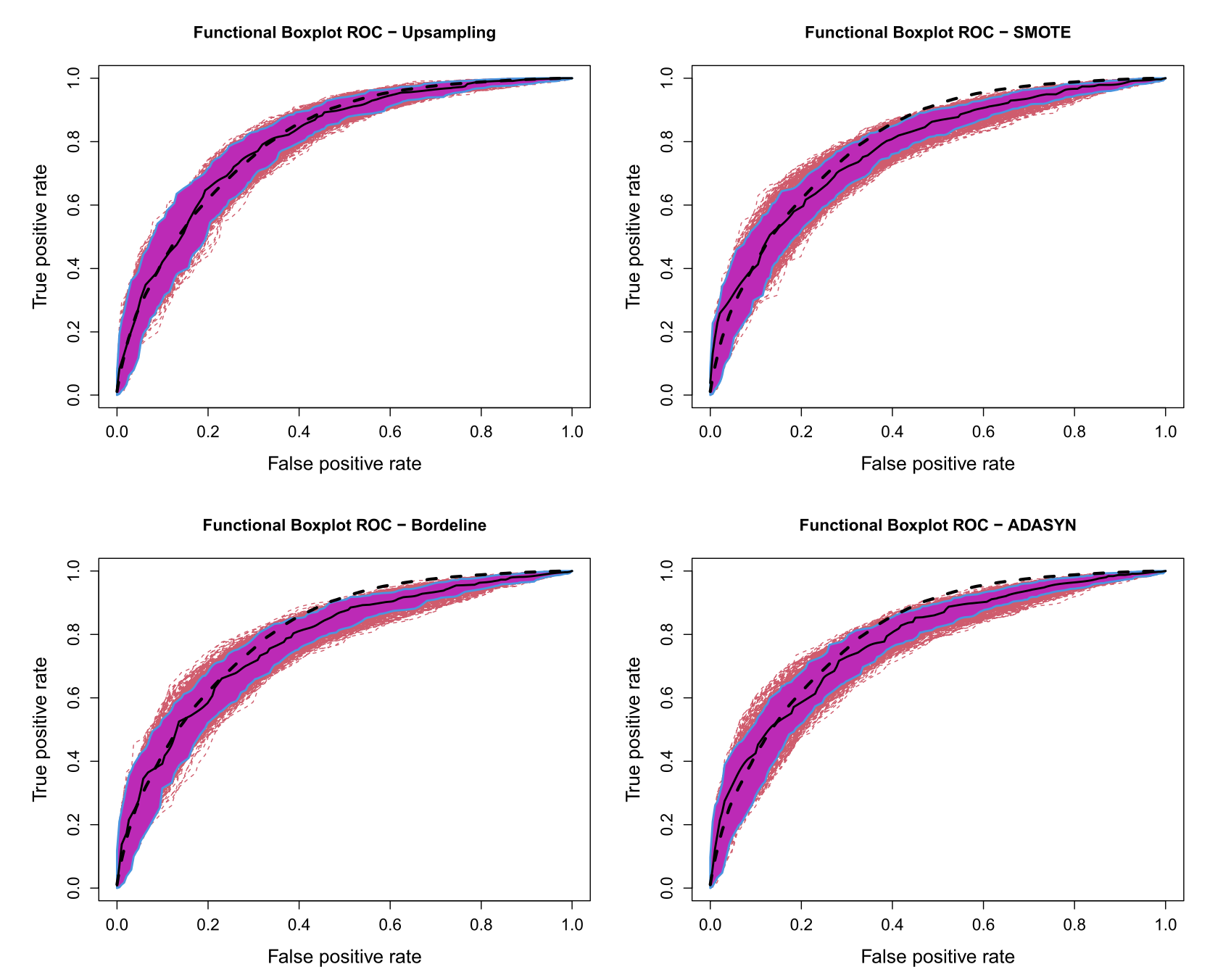
- 실제 ROC 커브를 그려봐도, 까만색 대시선이 기본 모델의 커브이고 나머지는 오버샘플링 모델의 커브의 인터벌, 중간값, IQR을 표시한 것인데 유의미한 차이가 없다는 것을 볼 수 있음