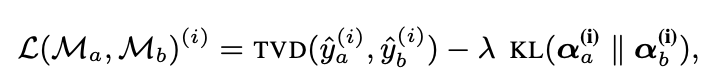Attention은 설명인가 아닌가

Attention의 설명력에 대한 논쟁들, Attention is not Explanation과 Attention is not not Explanation을 읽어보았습니다. 설명인가 아닌가, 설명이란 무엇인가…

어텐션은 설명이다?

어텐션(Attention) 매커니즘은 seq2seq RNN의 문제점을 해결하고 다양한 자연어처리 과제에서 뛰어난 성능을 보여 왔습니다. 어텐션이 무엇인가에 대한 자세한 내용은 이 글에서는 다루지 않겠지만, 간단히는 학습된 어텐션 가중치란 모델이 인풋 텍스트 시퀀스가 주어졌을 때 어떤 단어 혹은 어떤 토큰에 집중을 해야 하는지를 나타내는 값입니다. 어텐션은 단순히 모델이 더 판단을 더 잘하도록 도와줄 뿐만 아니라, 그 직관적인 속성 때문에 사후적으로 모델이 내린 판단에 대해 ‘어디를 보고’ 그렇게 예측했는지를 알 수 있게, 즉 매우 복잡한 모델의 내부 구조를 들여다보고 그 작동 방식을 해석할 수 있도록 해주는 것으로 알려져 있었습니다.

사랑? 어떤 단어를 보고 그렇게 생각했는데? 👀

설명이 아니다

Attention is not Explanation은 이러한 ‘설명으로서의 attention의 역할’에 의문을 제기합니다. 이 논문이 진행한 실험의 결과는 크게 다음과 같습니다.

1. 어텐션이 설명이라면 모델의 피쳐 중요도(Feature Importance)와 상관이 있어야 하는데, 없어
2. 어텐션이 설명이라면 모델이 다른 곳에 집중할 때 다른 예측을 해야 하는데, 동일한 모델 결과에 대해 다른 Adversarial Attention이 존재해

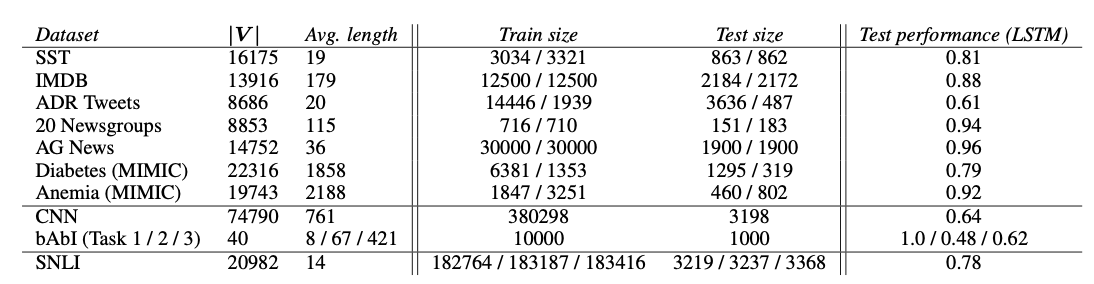
실험 2가지를 살펴보겠습니다. 두 실험 모두 총 8개의 데이터셋을 사용했습니다(텍스트 분류, QA, NLI 모두 포함).

• 사용한 데이터셋

어텐션과 피쳐 중요도 사이의 상관 부족

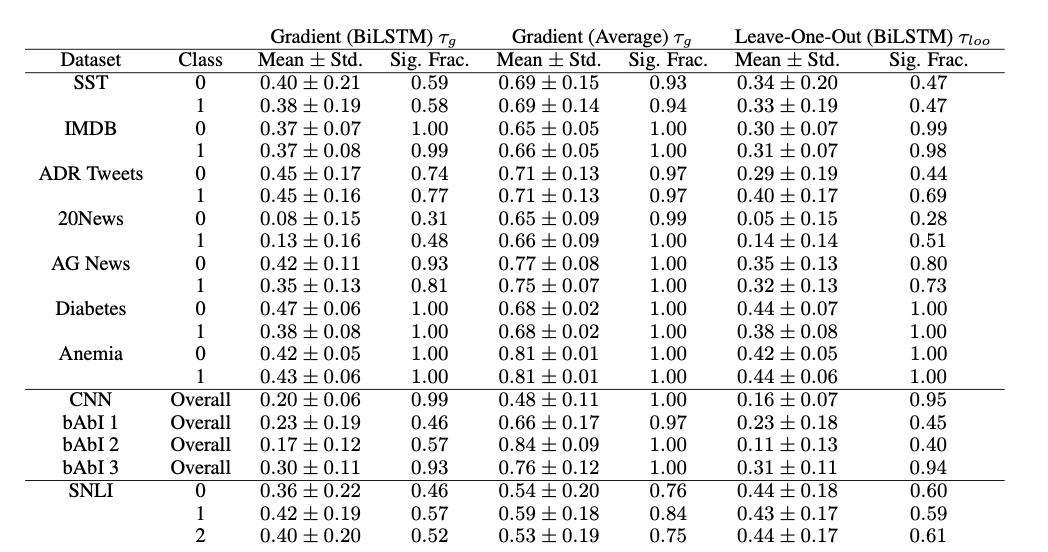
우선 첫번째 실험은 모델의 피쳐 중요도(feature importance)와 Attention을 비교합니다. 이때 사용한 변수 중요도 값은 gradient based measure와 leaving features out(LOO) 방식 2가지를 사용했습니다.

gradients는 기울기이고, LOO는 각 인풋을 뺐을 때 아웃풋과 빼지 않았을 때의 아웃풋을 비교해서 얼마나 차이가 나는지(TVD=Total Variance Distance)를 계산한 것입니다(차이가 많이 나면 해당 인풋이 예측에 많이 중요하단 뜻). 그리고 각각의 결과물과 어텐션의 상관(켄달 타우)을 구했고요.

잘 몰라서 뉴럴넷에 대해 원래 이런 값들을 중요도로 쓸 수 있나? 많이 쓰나? 싶었는데 논문이 짧게 언급하기로는 이런 값이 신경망 모델에 대한 어떤 해석을 제공하기에는 불충분하지만 각 피쳐의 영향력을 판단하는 값으로는 기능할 수 있다는 연구가 있대요.

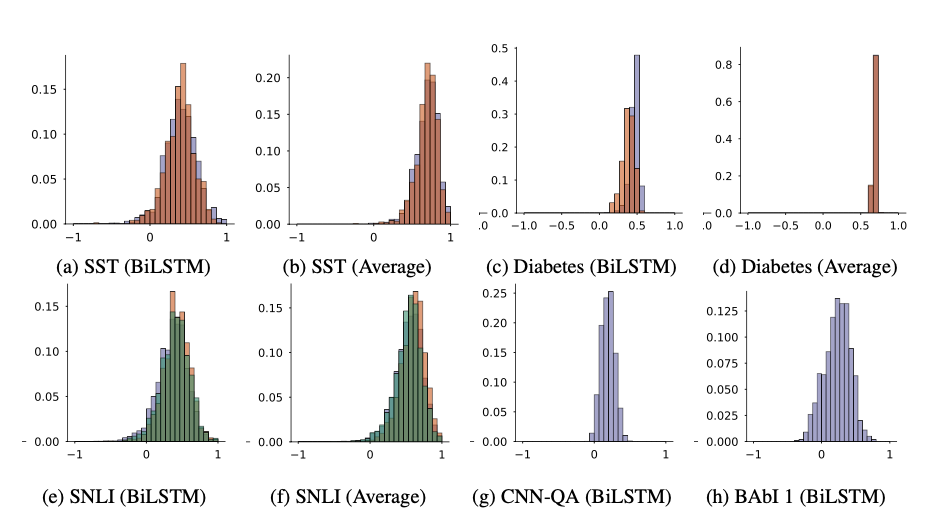
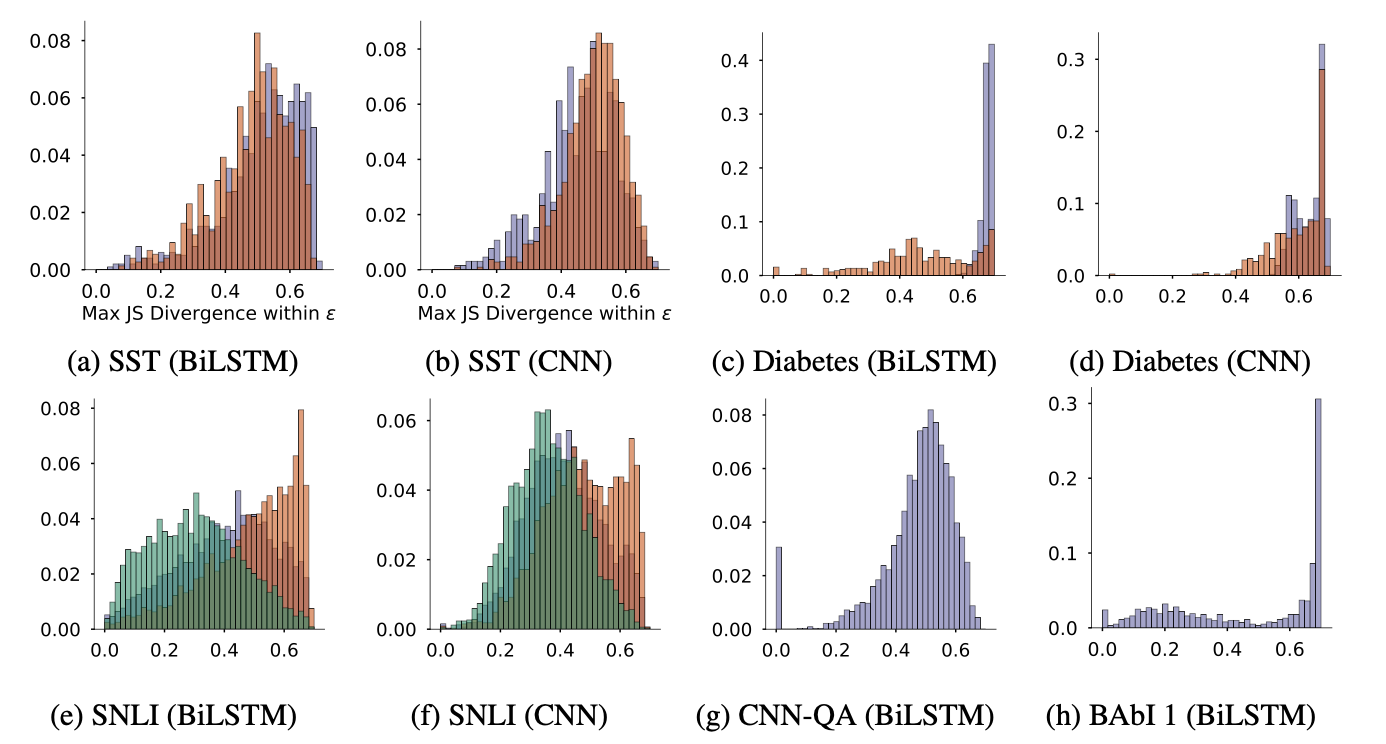
위 그림은 각 데이터셋에서 gradients와 attention weights의 상관관계의 히스토그램입니다. 색깔은 예측된 class에 따라 다르게 한 것이고요. 대부분 0.5 근처나 밑에서 몰려 있는 모양이고, 일부 데이터셋에서는 일관적으로 유의미한 상관이 있긴 했으나 약한 상관으로 보였다고 합니다. 즉, 어텐션과 피쳐 중요도는 그닥 상관이 없었다는 것이죠. LOO와 어텐션을 비교했을 때도 마찬가지였다고 합니다. 반면 LOO와 gradients는 상대적으로 서로 상관이 있다고 하고요. (셋 중 두 명이 기다 하고 나머지 한 명이 아니다 하면 아무래도 기지 않겠느냐.. 라는 논리)

• 전체 상관관계

동일한 결과에 대한 다른 어텐션 분포의 존재

좌측은 원래 어텐션 분포 ↔ 우측은 생성된 다른 어텐션 분포에서 나온 결과이며, 하이라이트된 부분이 weight가 높은 단어입니다. 완전히 다른 어텐션 분포 하에서 모델이 양측에서 동일하게 낮은 예측값 0.01(=이 리뷰는 부정적임)을 보이는 상황이죠. waste에 집중했을 때랑 was에 집중했을 때랑 결과가 같다면, waste에 하이라이팅을 하는 게 예측값 0.01이라는 결과물에 대한 설명이라고 할 수 있을까요?

이걸 보이기 위해 두번째 실험은 위 예시처럼 어텐션을 막 바꿔보자! 에서 출발합니다. 막 어떻게 바꾸냐 하면 진짜 막 바꿉니다. 모델에서 생성된 attention weight의 인덱스를 그냥 랜덤하게 섞는 것이죠. 그 다음에 그 중에서 원래의 어텐션과 가장 다르지만 같은 결과를 도출하는 또다른 어텐션을 찾습니다(Adversarial Attention).

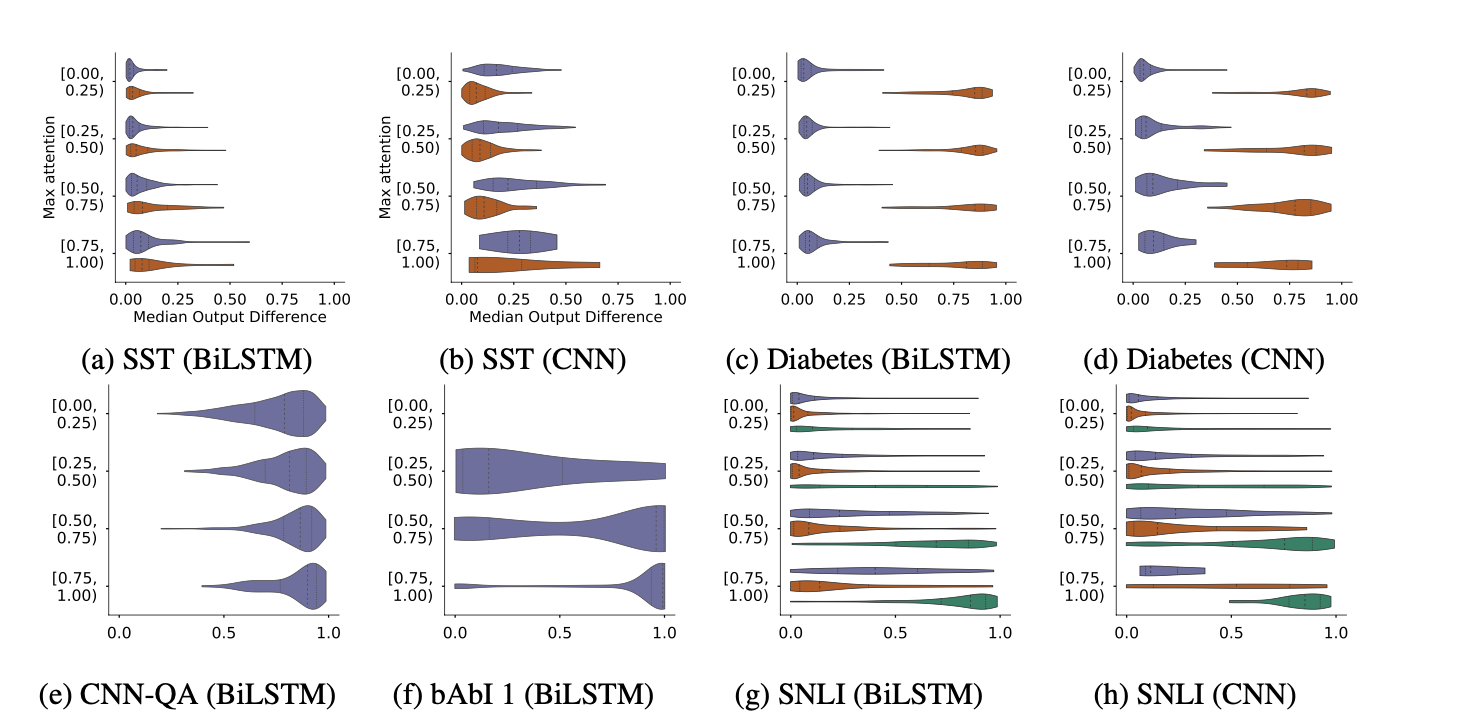
우선 어텐션을 랜덤하게 섞으면 예측 결과가 많이 달라지는지를 기존 분포의 어텐션의 최대값에 따라 살펴봅니다.

이렇게 하는 이유는, 기본적으로 어텐션 분포의 최대값이 굉장히 튀는 (peaky한) - 즉 특정 인풋에 어텐션이 쏠리는 경우, 어텐션을 앞서 말한 것처럼 랜덤하게 바꾸어버리면 예측 결과가 많이 달라져야 하지 않겠느냐는 전제 하에서입니다. 예를 들어 재미있기만 한데 별점이 왜 이래? 다들 기대를 너무 많이 한 듯 이 인풋이고, 원래 모델이 재미있기만에 매우 큰 weight 값을 주고 이 리뷰를 긍정적일 가능성이 높다고 예측했다면, 이런 케이스는 이렇게 명백하게 weight가 높은 인풋이 존재하지 않는(전체 토큰 weight가 다 고만고만한) 경우에 비해서 랜덤하게 weight를 변형했을 때 영향을 크게 받을 수밖에 없다는 것이죠.

이 그림의 y축이 바로 어텐션의 최대값이 위치한 구간을 나타냅니다. 따라서 가장 하단의 [0.75 ~ 1.00)이 바로 가장 어텐션 최대값이 매우 큰 경우입니다. x축은 원래 모델의 예측과 랜덤하게 섞은 어텐션을 사용한 예측 간 차이이고요. 많은 데이터셋에서 원래 어텐션의 최대값이 큰데도, 즉 특정 인풋에 강하게 주목한 모델인데도 불구하고 랜덤하게 바꾼 어텐션 분포 하에서 원래의 예측과 크게 달라지지 않는 케이스가 발견되었다는 것을 확인할 수 있습니다.

다음은 이제 Adversarial attention을 만들어 볼 차례입니다. 이 연구의 논리는 기본적으로 counterfactual의 접근입니다. 인과관계 판단이랑 비슷한데요, 어느날 우유를 먹고 배가 아파서 난 유당불내증인가? 했는데, 만약 다음날 우유를 안 먹었는데도 배가 아프다면 어 우유가 문제가 아니구나! 하게 되겠죠. 이런 접근의 목적은 모델의 아웃풋인 예측 결과를 크게 바꾸지 않으면서 가능한 한 기존 어텐션과 가장 큰 차이가 나는 다른 어텐션 분포를 찾는 것입니다. 그런 어텐션을 찾을 수만 있다면 어텐션이 신뢰 가능한 설명으로서 기능한다는 기존의 인식을 반박할 수 있겠다는 것이고요.

• 어떻게 찾을 것인지!

예측 결과를 크게 바꾸지 않으면서의 기준은 미리 아주 작은 epsilon 값(예를 들면, 0.01)을 정하고, 기존 예측 결과와 새로운 예측 결과의 차이가 그 값보다 작으면 달라지지 않았다고 봅니다.

그리고 기존 어텐션과 새로운 어텐션의 차이는 확률분포 간 거리/차이를 나타내는 JSD(Jensen-Shannon Divergence)라는 메트릭을 쓰는데, 이건 보다 더 잘 알려진 KL Divergence(Kullback-Leibler Divergence)의 symmetric한 버전입니다. (뭔 말이냐면, KLD는 x와 y의 거리 ↔ y와 x의 거리가 다르게 나오는데 이걸 같게 만들어준 값이라는 뜻입니다.)

JSD의 상한이 0.69임을 고려합시다. 이 그림은 전부 모델 아웃풋 차이가 우리가 앞서 정한 epsilon 밑으로 떨어지는, 즉 모델 아웃풋이 달라지지 않았다고 볼 수 있는 결과만 그린 것입니다. x축이 JSD이고요. 그러니 JSD가 아주 크면서 (=기존 어텐션과 최대한 차이가 나면서) 아웃풋은 같은 adversarial attention을 어렵지 않게 찾을 수 있었다는 결론이 나오네요.

설명이 아닌 것은 아니다

이어서 읽어 볼 논문은 Attention is not not Explanation으로, 위 Attention is not Explanation의 일부 주장을 다른 실험을 통해 반박하고 있습니다. 앞선 논문의 2가지 주장 중 첫번째(피쳐 중요도랑 상관이 없음)은 오케이라고 하지만, 두번째 실험은 뭔가 좀 잘못됐다는 것인데요. 두번째 실험의 각 논지에 다음과 같이 문제를 제기합니다.

1. Attention을 랜덤하게 섞어도 아웃풋이 별로 안 달라지던데 → 어텐션은 모델에 독립적인 게 아니라 딸려오는 건데, 그렇게 따로 떼어서 랜덤으로 막 섞어서 얻은 결과가 무엇을 말해주나? Adversarial attention을 잘못 만들었음
2. 똑같은 아웃풋을 내는 다른 Attention이 존재하던데 → LSTM은 마지막 층에서 지금까지의 인풋을 합쳐셔 하나의 예측 결과값을 내고, 그 과정에서 다양한 방식으로 어텐션과 같은 모델 구성요소들을 고르게 됨. 이진분류라면 아웃풋은 1 또는 0인 반면 인풋 토큰은 수백 수천개인데, 이렇게 자유도가 높은 연산 과정에서 입맛에 맞는 반례를 찾아내는 건 놀라운 결과가 아님

한마디로 실험 세팅이 잘못되었다는 지적입니다. 이 논문은 그 실험을 제대로된 세팅으로 다시 해보기 전에, 우선 어텐션과 모델 아웃풋의 관계를 이것저것 뜯어보고 들어갑니다. 에피타이저로 실험 셋업 3가지의 요약을 한번 보겠습니다. 앞서 문제로 언급한 자유도가 높은 실험 환경을 조금씩 좁혀 나가는 과정이라고 보면 됩니다.

1. 어텐션이 효과가 없는 경우는?
   • 데이터나 태스크에 따라서 어텐션이 효과가 없는 경우도 있을 수 있음 = 애초에 어텐션이 별 의미가 없는데 설명력이 있냐 없냐를 왜 따지나?
   • 베이스 어텐션 모델의 결과와 모든 attention weight를 균등 분포로 갈아끼워버린 모델의 결과를 비교해서 별 차이가 없다면, 그런 데이터는 실험 대상에서 빼야 함
   • 즉, AgNews와 20News 같은 데이터는 논쟁의 대상에서 아웃
2. 어텐션의 변동이 큰 경우는?
   • 원래 좀 어텐션이 크게 왔다갔다 하는 놈이면 새로 바꾼 어텐션과 기존 어텐션이 엄청 떨어져 있는 게 그다지 놀라운 일은 아니지 않나?
     • 랜덤 시드 설정을 통해 기본적인 모델의 어텐션 변동 정보를 먼저 파악해야 adversarial attention의 효과를 제대로 볼 수 있음
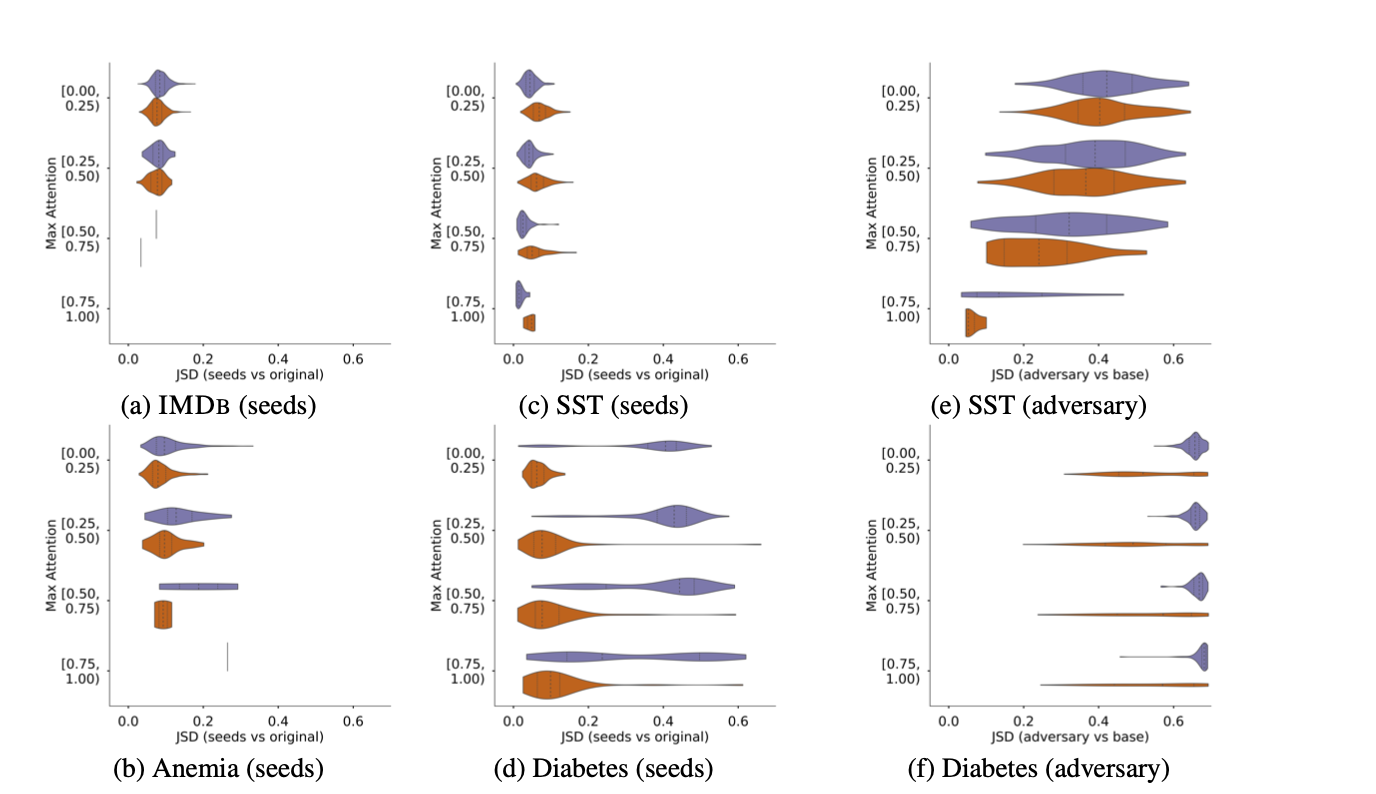
   • a~d는 랜덤 시드 설정을 통해 어텐션 분포를 변화시켜 베이스 분포와 비교한 JSD 그림이고, e와 f는 앞선 논문의 adversarial attention을 베이스 분포와 비교한 JSD 그림
   • Diabetes 데이터셋의 경우, 앞선 논문의 방식대로 만든 adversarial attention과 베이스 분포 간 JSD가 매우 큰 케이스들이 보이지만(f), 이 그림만 보는 게 아니라 원래 랜덤 시드 설정을 통해서도 큰 JSD가 나올 수 있다는 사실을 알면(d) 별로 놀랍지 않음
3. 깔끔하게 어텐션의 효과만 보고 싶다면?
   • LSTM은 그 구조상 예측이 주변 토큰에 종속적인 representation을 활용하므로, 모델의 성능이 어텐션 모듈에서 오는 건지 거기서 오는 건지 잘 모를 수 있음
   • 따라서 아예 모델을 LSTM에서 다음처럼 생긴 MLP(다층 퍼셉트론) 구조로 바꿔 봄
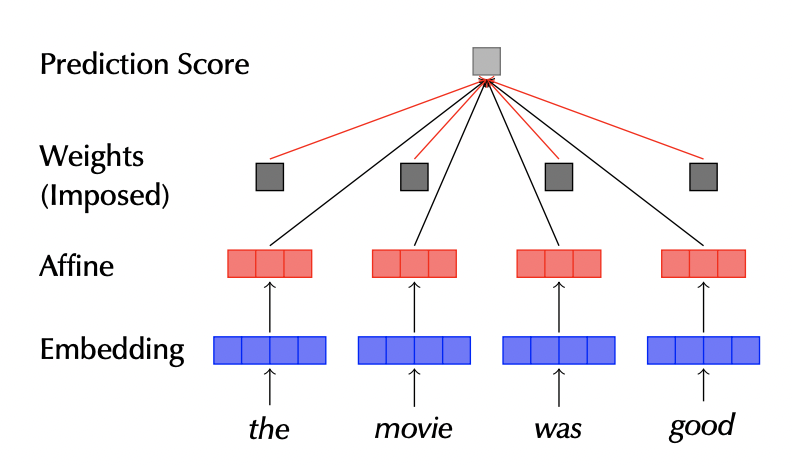
   • 이때 Weights를 어떻게 설정할지를 4가지로 실험하는데
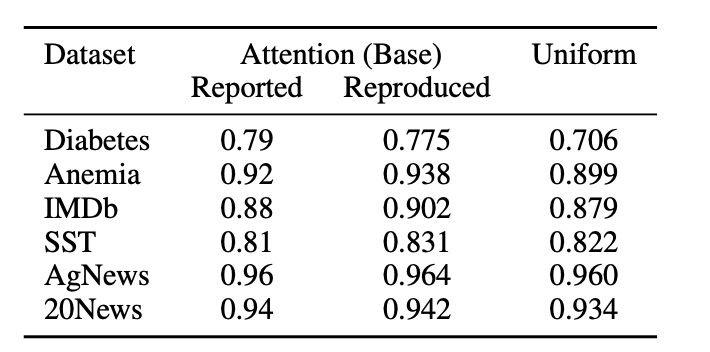
     1. Uniform : 즉 다 똑같은 weight = 어텐션 없는 모델
     2. Trained MLP : MLP 구조에서 알아서 weight을 학습하도록 둔 모델
     3. Base LSTM : MLP 구조에서 기존 베이스 LSTM 에서 학습한 pre-trained attention 사용 (*이름을 헷갈리게 지어놨는데 LSTM 모델이라는 게 아님!)
     4. Adversary : 다음 섹션에서 설명할, 제대로 만든 adversarial attention 사용
   • 그 결과, 성능은 어텐션 안 쓰기 < MLP가 직접 학습한 weight < LSTM에서 학습된 weight
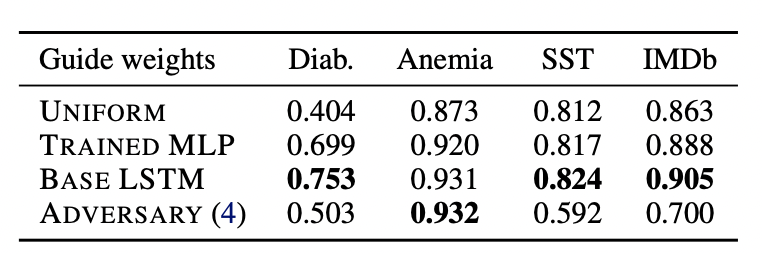
     • c의 성능이 좋았다는 게 말해주는 사실은 어텐션 모듈이 그 자체로 중요하다는 것. 토큰 간의 관계를 고려하지 못하는 MLP 구조는 기본적으로 단어 간 맥락 정보를 모르기 때문에 LSTM 어텐션이 제공하는 정보를 유용하게 사용함 (= LSTM이 학습한 어텐션은 LSTM 모델 없이도 각 토큰에 대한 유의미한 정보를 인코딩하고 있음)

‘제대로’ Adversarial Attention을 만들면 다른 결과가 나올걸

Attention is not Explanation 이 하고자 했던 실험이 잘못되었다고 주장한 만큼, 이제 같은 실험을 제대로 진행해 볼 차례입니다.

이 연구는 앞선 논문과는 달리 Adversarial attention을 따로 학습을 시킵니다. 어텐션은 모델에 딸려 오는 거고 모델과 분리해서 실험하는 건 무의미하다고 비판한 만큼, 새로운 어텐션을 만들기 위한 아예 별도의 모델을 만드는데요. 이 모델의 학습 목표는, 모든 데이터에 대해 기존 모델과 유사한 예측값을 보이면서 어텐션은 다르게 하는 것입니다. 즉 이 모델이 줄이고자 하는 loss function을 아래와 같이 만듭니다.

앞의 부분인 TVD는 예측 아웃풋 간의 차이를 나타내고 뒤의 항은 기존 어텐션과 새로운 어텐션 분포 간 차이를 나타냅니다. 이때 람다는 하이퍼파라미터로서 JSD와 TVD 사이의 tradeoff를 조절하는 용도이고요.

눈여겨볼 부분은 이 loss function이 새로 훈련시키는 모델의 진짜 성능(라벨 맞히기)는 고려하고 있지 않다는 것입니다. 이 따라쟁이 모델은 기존 모델의 예측을 따라하려고 하지 (TVD를 줄이기) 실제 라벨을 맞히려고는 하지 않습니다. 그래서 이 모델이 학습한 어텐션을 MLP 에다가 붙이면 (저 위의 표에서 ADVERSARY(4)로 기재된 마지막 행) 많은 경우 성능이 처참해집니다. 인풋과 아웃풋의 관계를 학습하지 않고 기존 모델의 결정만 따라하려 했으니까요.

어쨌든 우리의 주안점은 무엇보다 JSD(어텐션의 차이)와 TVD(모델 예측의 차이)입니다. 만약 JSD를 x축에, TVD를 y축에 놓는 2차원 플랏을 그린다면, 그 플랏이 어떻게 생긴 선인가에 따라서 앞선 논문이 제시한 주장에 대한 평가가 정해질 것입니다.

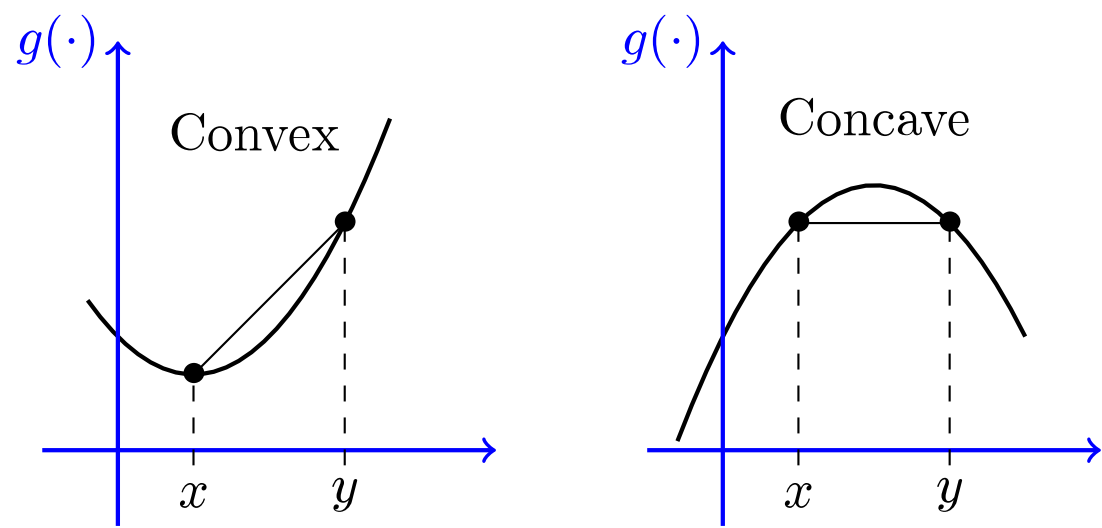
• 그 선이 convex 함 = 어느 정도까지는 JSD를 자유롭게 늘려도 TVD가 많이 늘어나지 않아(아웃풋이 크게 달라지지 않아) = 앞선 논문의 주장과 일치
• 그 선이 concave 함 = JSD가 조금만 늘어나면 TVD도 확 늘어나(아웃풋이 확 달라져)
• 참고로 convex와 concave는 이런 겁니다(볼록, 오목).

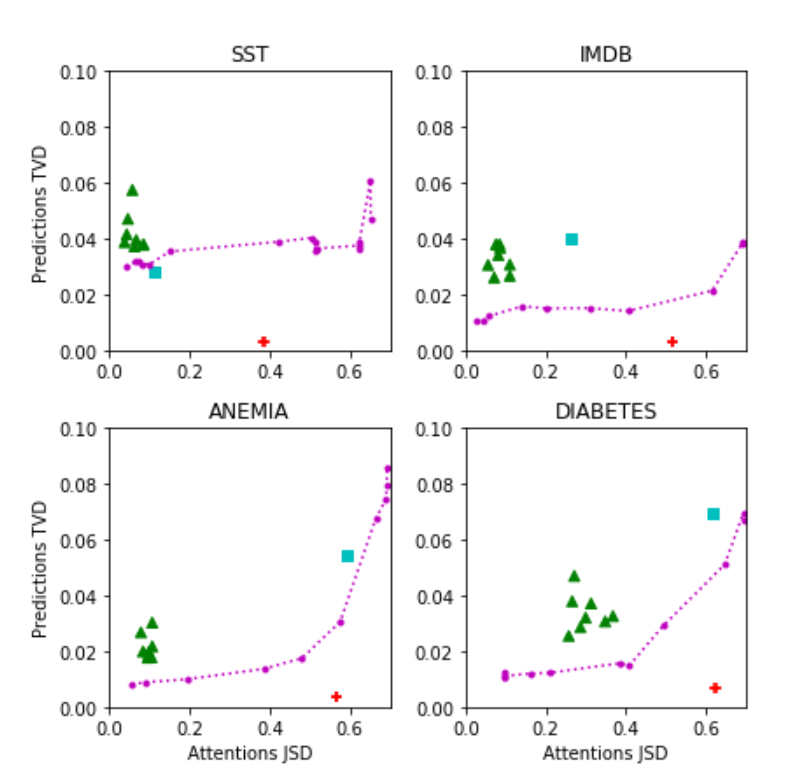이게 바로 그 2차원 플랏이자 이 논문의 결과를 가장 잘 요약해주는 그림이 되겠습니다. 색깔이 다채로우므로 풀어서 설명하면,

• 분홍색 원/선: 위 방식으로 만든 adversarial attention의 결과 / JSD에 따른 TVD 추세선
• 초록색 세모: 랜덤 시드 설정으로 모델 아웃풋의 변동을 파악한 것
• 파란색 네모: 어텐션을 uniform 분포로 갈아끼웠을 때, 즉 어텐션을 사용하지 않을 때의 결과
• 빨간색 십자: 이전 논문이 제시한 adversarial attention의 결과를 그대로 따라한 것

일단 선 자체는 convex합니다. 어느 정도까지는 JSD가 늘어나도 TVD가 크게 증가하지 않는 모습입니다. 다만 JSD를 매우 크게 가져가게 되면 그에 따른 상당한 TVD 증가 양상을 확인할 수 있으며, 무엇보다 이전 논문의 결과를 그대로 따라한 빨간 십자의 위치는(JSD를 극대화했으나 TVD는 거의 늘어나지 않는 케이스) 추세선과 매우 동떨어져 있어, 이전 논문의 실험이 정말 엄밀하게 전체적인 경향성을 보였다기보다는 자유도가 매우 높은 실험에서 결론에 맞는 케이스를 뽑아서 제시한 것에 가깝다는 사실을 보여줍니다. 이 논문은 이전 논문이 “과장했다(exaggerate)”라는 표현을 쓰고 있네요.

결국은 설명이 대체 무엇인가의 문제

설명가능하다(explainable)이라는 말은 그 하위의 여러 가지 서로 다른 개념을 포함하는 umbrella term이라고 합니다.

1. Transparency
2. Explainability
3. Interpretability

각각의 개념, 그리고 총체적인 설명가능하다는 개념을 어떻게 정의하느냐는 사용자마다 그리고 유즈케이스마다 충분히 달라질 수 있는 부분이고 관련된 연구들도 활발하게 진행되고 있는 중입니다.

예를 들어 Transparency의 개념을 어떤 연구는 ‘인간이 이해 가능한 구성개념(Construct)와 대응 가능한 모델 내부의 특정 요소가 존재하는가?’로 파악합니다. 이런 접근으로 보면 NLP 모델에서 어텐션은 모델이 내부적으로 어떻게 작동하는지를 보여주는 값으로서 충분히 transparency를 지니고 있는 것 같습니다.

또 어떤 연구는 설명가능성이란 모델의 의사결정 과정이 재구성될 수 있는지를 말해주는 것이라고 말하기도 합니다. 사람은 어떤 결정이나 행동을 하고, 사후에 그것을 합리화하는 논리를 세우는데 이를 모델에도 똑같이 적용해볼 수 있습니다. 우리가 어떤 스토리를 만들어서 (내가 감자전을 부쳤을 때 마침 냉장고에 막걸리도 있고 비가 추적추적 오더라고…) 그래서 그렇게 한 거야, 라고 말하지만 그게 꼭 그 당시 우리 머릿속에서 일어난 프로세스를 정확하게 재현한 건 아닐 수 있죠(그냥 저녁을 안 챙겨먹어서 배가 고팠음). 이런 입장에서 말하는 설명은 그럴 듯한(plausible) 이유를 찾는 것이며 그 이유가 꼭 유일하고, 배제적이고, 충실한(faithful) 하나의 이유일 필요는 없습니다. 이런 정의를 받아들이면, 복수의 다른 설명이 존재한다는 사실이 그 중 하나하나의 퀄리티를 공격하지 않기 때문에, Attention is not Explanation의 논지처럼 유일한 설명이 아니므로 설명이 아니라는 주장은 유효하지가 않은 거죠. 그리고 설명에 대한 인간의 평가도 필요한 부분이 되겠고요.

물론 인풋의 특정 요소에 대한 높은 어텐션 값이 과연 그 모델이 그런 예측을 하도록 만들었는가? 는 매우 중요한 질문이고, counterfactual한 접근도 의미가 있다고 생각합니다. 그건 Attention is not not Explanation의 저자들도 동의하는 사실입니다. 어쨌든 counterfactual attention이 존재한다는 사실은, 우리가 어텐션 값만 들여다봤을 때는 결국 인풋과 아웃풋 간의 관계를 명확하게 규명하기 어려울 수 있다는 의미이니까요.

Attention is not not Explanation은 마지막 섹션에서 Attention is all you need it to be 라는 쿨한 문장으로 마무리됩니다. 그래서 당신이 정의하는 설명가능성의 개념은 어디까지인가, 아직은 이 질문이 답인 것 같기도 합니다.