DBSCAN 이해하기
밀도 기반 클러스터링 방식인 DBSCAN의 알고리즘과 장단점, 구현 방식을 들여다보는 글입니다.
DBSCAN은
오늘의 주제인 DBSCAN(Density-Based Spatial Clustering of Application with Noise)은 무려 96년도 논문(A density-based algorithm for discovering clusters in large spatial databases with noise)에서 제시된 클러스터링 알고리즘입니다.
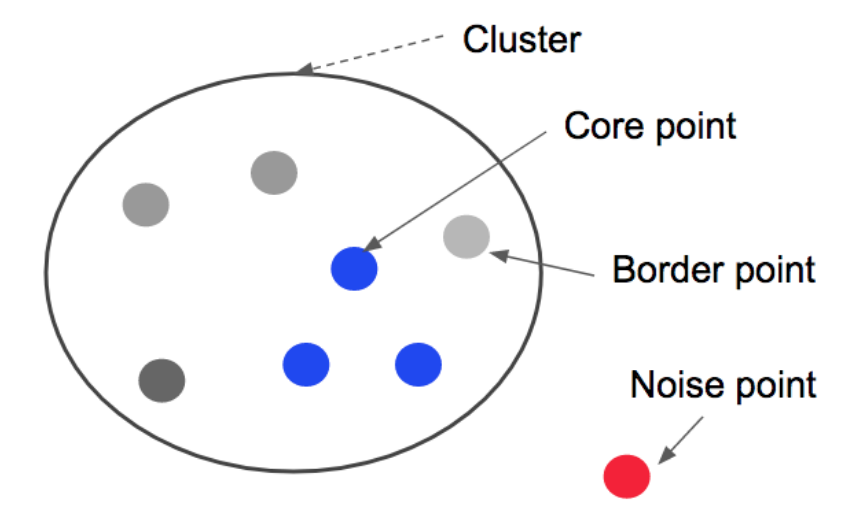
그대로 번역하면 노이즈가 있는 대규모의 데이터에 적용할 수 있는 밀도 기반의 군집화 알고리즘이란 뜻이죠. 이때 밀도 기반이라는 것은, 클러스터를 찾을 때 데이터 포인트들이 밀도 있게 모여 있는 곳을 찾겠다는 것입니다. 그렇게 하기 위해서 우리는 ‘밀도 있다’라고 보는 거리의 특정 수준을 정합니다. A와 B도 그 수준보다 가까운 거리에 있고, B와 C도 그 수준보다 가까운 거리에 있다면 A, B, C는 우리 기준에서 ‘밀도 있게’ 모여 있다고 볼 수 있겠습니다. A와 C는 가깝지 않아도 그 사이에 연결해주는 B가 있다면 괜찮아요.
밀도 기반 v.s. 중심과의 거리 기반
DBSCAN은 위 그림처럼 단순히 가까운 거리로 묶는 게 아니라 가깝게 모여 있고, 연결되어 있는 데이터들을 묶고 싶을 때 유용합니다.
명백한 DBSCAN의 장점은 클러스터의 개수를 미리 지정할 필요가 없으며 이상치(Noise)를 효과적으로 제외할 수 있다는 것입니다. 우리가 정한 ‘밀도 있다’라는 기준보다 가까운 다른 이웃이 없는 데이터포인트가 있다면, DBSCAN은 이 데이터를 어떤 클러스터에도 넣지 않고 노이즈로 분류합니다.
이런 이유 때문에 저는 사실 회사에서 군집화 목적으로 DBSCAN을 꽤 자주 씁니다. 아니 사실 거의 DBSCAN만 씁니다. 처음 보는 데이터에 대해 군집이 몇 개일지(군집이 존재하기는 하는지) 전혀 알 도리가 없을 뿐더러, 사실상 A라는 집단과 크게 비슷하지도 않은데 ‘그나마’ A의 중심점에 가깝다는 이유로 특정 데이터포인트 x를 A에 배정할 경우(= K-means 같은 걸 쓸 경우) 리스크가 발생하는 업무를 하고 있기 때문입니다. 즉, 제가 찾는 집단과 충분히 가깝지 않은 데이터는 배제할 수 있다는 것이 가장 큰 장점입니다.
스몰사이즈 군집에 노이즈는 빼고 주세요 감사합니다.
어떻게 하나
작동 방식
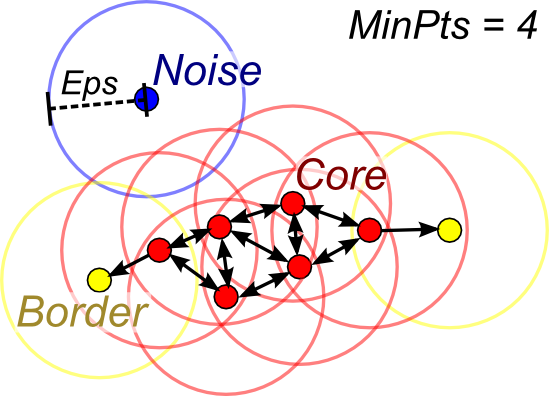
DBSCAN 알고리즘은 상당히 간단하며, 미리 정해야 하는 것은 반경의 크기(= eps) 와 최소 군집의 크기(=MinPts) 이 2가지 입니다. 반경의 크기란 아까 언급했던 얼마나 가까워야 연결되었다고 볼 것인지에 대한 거리 값을 말하고, 최소 군집의 크기란 몇 개가 연결되어 있어야 군집으로 볼 것인지 데이터의 개수를 뜻합니다. 즉 MinPts가 10이라면, 6개 데이터가 아무리 오밀조밀 잘 모여있다고 한들 우리가 찾는 군집으로 보지 않고 노이즈로 보겠다는 것입니다.
전체 작동 방식은 다음과 같이 요약됩니다.
- 랜덤하게 데이터포인트를 돌아보자.
- 방문할 때마다 그 포인트에서 다른 모든 데이터포인트까지의 거리를 계산한다.
- 이때 거리 메트릭은 어떤 방법을 사용해도 된다. 거리 메트릭이 하나의 파라미터가 될 수도 있겠다.
- 내가 정한 반경(eps)보다 작은 다른 데이터포인트가 내가 정한 최소 군집 크기(MinPts ) -1 이상만큼 있다면 이 데이터포인트는 Core Point가 된다. 아니면 노이즈다(하지만 이후에 다른 Core Point에 가까이 있는 Border Point로 확인될 경우 그 클러스터로 들어갈 수도 있다).
- 돌다 보면 하나의 클러스터에 여러 개의 Core Point가 생길 수도 있다. 연결되어 있다면 그냥 같은 클러스터로 분류해주면 된다.
- Border Point는 Core Point 입장에서는 eps보다 가까워서 클러스터로 분류는 되었지만, 자기 입장에서는 eps보다 가까운 데이터가 MinPts보다 적은 데이터를 말한다.
MinPts=4 이면 Core가 되기 위해 반경내에 가까운 3개가 있어야 함
- 어디에도 연결되지 못했거나 몇 개가 연결되어 있어도 최소 군집 크기를 충족하지 못하면 노이즈로 분류한다.
- 모든 데이터포인트가 클러스터이거나 노이즈일 때까지 반복한다.
사람에 따라서는 의사코드를 보는 게 이해가 빠를지도 모르겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
DBSCAN(DB, distFunc, eps, minPts) {
C := 0 /* Cluster counter */
for each point P in database DB {
if label(P) ≠ undefined then continue /* Previously processed in inner loop */
Neighbors N := RangeQuery(DB, distFunc, P, eps) /* Find neighbors */
if |N| < minPts then { /* Density check */
label(P) := Noise /* Label as Noise */
continue
}
C := C + 1 /* next cluster label */
label(P) := C /* Label initial point */
SeedSet S := N \ {P} /* Neighbors to expand */
for each point Q in S { /* Process every seed point Q */
if label(Q) = Noise then label(Q) := C /* Change Noise to border point */
if label(Q) ≠ undefined then continue /* Previously processed (e.g., border point) */
label(Q) := C /* Label neighbor */
Neighbors N := RangeQuery(DB, distFunc, Q, eps) /* Find neighbors */
if |N| ≥ minPts then { /* Density check (if Q is a core point) */
S := S ∪ N /* Add new neighbors to seed set */
}
}
}
}
이때 RangeQuery 는 모든 데이터포인트에 대해 eps 보다 가까운 이웃을 찾습니다.
1
2
3
4
5
6
7
8
9
RangeQuery(DB, distFunc, Q, eps) {
Neighbors N := empty list
for each point P in database DB { /* Scan all points in the database */
if distFunc(Q, P) ≤ eps then { /* Compute distance and check epsilon */
N := N ∪ {P} /* Add to result */
}
}
return N
}
Scikit-learn 문서 뜯어보기
Python으로 DBSCAN 써보는 가장 간단한 방법은 scikit-learn입니다. 요렇게 쓰면 됩니다(쓰기 전에 데이터 스케일링이 필요합니다).
1
2
3
from sklearn.cluster import DBSCAN
clusters = DBSCAN(eps = 0.3, min_samples = 5).fit_predict(data)
eps와 min_samples (MinPts) 외의 필수는 아니지만 지정할 수 있는 파라미터 중 중요한 것은 다음과 같습니다.
metric: 사용하는 거리 메트릭 (디폴트:euclidean)- euclidean, manhattan, chebyshev, minkowski, wminkowski, seuclidean, mahalanobis 등
sklearn.metrics.pairwise_distance가 허용하는 메트릭 precomputed일 경우 인풋 데이터가 원본 데이터가 아닌 모든 쌍의 거리가 미리 계산된 상태의 거리값이라고 생각하고 알고리즘 적용
- euclidean, manhattan, chebyshev, minkowski, wminkowski, seuclidean, mahalanobis 등
algorithm: 최근접 이웃을 찾는 알고리즘 (디폴트:auto)- brute, kd_tree, ball_tree, auto(3개 중 최적을 선택)
DBSCAN의 fit 메서드를 들여다보면 내부에서 Nearest Neigbors 를 이용한다는 사실을 알 수 있습니다. DBSCAN의 algorithm 파라미터는 사실 이 Nearest Neighbors에 넣을 파라미터입니다.
- brute force : 모든 쌍의 거리를 계산하여 탐색
- KD Tree : 트리 구조를 사용해서 모든 거리를 계산하지 않고 비용을 줄여 탐색
- 기본 아이디어는 만약 A가 B와 굉장히 많이 떨어져 있고, B는 C와 굉장히 가깝다면 A와 C도 멀리 떨어져 있을 것이므로 명백하게 그 거리를 전부 계산할 필요는 없다는 것
- Ball Tree : 마찬가지로 트리 구조 사용, 트리를 만드는 비용은 크지만 고차원의 데이터에서 KD Tree보다 좋은 성능으로 탐색
이웃 탐색 시 삼각부등식( $ x + y \le x + y $ )을 이용해 이웃 후보를 효율적으로 쳐내는 방식 (한번 거리를 계산할 때마다 다른 포인트들의 상한/하한이 딸려오므로)
즉 이 방법을 통해 각 데이터의 근접 이웃의 개수를 셈으로써 Core Point 여부를 결정하는 것이 DBSCAN 알고리즘의 핵심이 되겠습니다.
스파크에서는?
스파크에서 DBSCAN 쓸 때는 pandas udf 내에서 sklearn 호출하는 방식으로 주로 썼는데 데이터 크기에 따라 엄청 느려질 수도 있거든요. 참고로 DBSCAN의 복잡도는 인덱스 구조가 잘 돼 있으면 O($n\log n$)이고 최악의 경우에는 O($\log n^2$)입니다). 그래서 언젠가 스칼라 implementation을 좀 찾아봐야지 생각만 하고 제가 스칼라를 잘 몰라서 그냥 미뤘었는데요. 저 NN 알고리즘처럼 거리 계산을 효율적으로 할 수 있는 구현 + graphframes 사용해서 eps 기준으로 자르고 그래프 만들어서 connected components 쓰면 UDF 안 쓰고 빠르게 할 수 있지 않을까 라는 생각이 들었습니다.
검색해보니, 이분이 그렇게 pyspark로 구현하신 것 같군요. 근데 역시 작은 데이터셋에서는 sklearn보다 느리다고. (큰 데이터를 가져다가) 한번 베껴써봐야겠어요.
An Efficient Implementation of DBSCAN on PySpark
파라미터는 어떻게 정하나
클러스터의 개수를 지정할 필요가 없는 건 장점이지만 DBSCAN도 파라미터 설정이 매우 중요합니다. 만약 반경의 크기를 너무 크게 잡아버리면 모든 데이터포인트가 다 연결되어 버릴 수 있습니다. 너무 작게 하면 다 노이즈가 되어버릴 수도 있고요. 따라서 DBSCAN을 사용할 때는 여러 값의 eps로 실험해보는 과정이 필요합니다. 최소한 일단 저는 그렇게 쓰긴 합니다. 실험을 여러 번 한 다음에 결과물을 보고 제 얄팍한 도메인 지식에 의존하여 이 정도면 납득 가능하게 잘 묶이는군 하고 결정하고 쓰는 편…
그럴싸해 조와 eps 0.5 너로 정했어
하지만 논문 저자들이 제안한 파라미터 결정을 위한 방법도 있기는 있습니다. 살짝 살펴봅시다.
MinPts 정하기
- 논문 저자들에 따르면 MinPts = 4 와 5는 아래서 소개할 k-dist 플랏 차이가 거의 없고 MinPts를 올리면 계산 비용이 그에 따라서 커지므로 4가 좋겠다.
- rule of thumb로 데이터셋 차원 k를 MinPts로 쓰거나, 2$*$k를 쓰기도 한다.
- 노이즈가 많을수록, 데이터 크기가 클수록 MinPts를 크게 설정하면 좋다.
eps 정하기
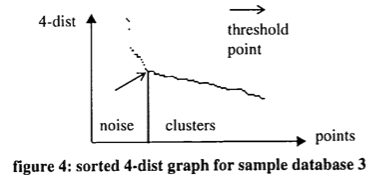
원 논문은 eps에 대해서는 Elbow method를 제안합니다. 즉 k-distance 플랏을 그린 다음에 팔꿈치를 찾는 것입니다.
- k-distance 플랏이 뭐냐면
- 일단 k-distance는 정해진 MinPts k개에 대해 각 데이터포인트들마다 k개 가장 가까운 다른 데이터들(k-nearest neighbor)까지의 평균 거리를 말한다.
- 모든 데이터포인트에 대해 k-distance를 구해서 순서대로 정렬하고, y축이 k-distance, x축이 각 데이터포인트가 되도록 그린 플랏을 k-distance 플랏이라고 하겠다.
그리는 법
1 2 3 4 5 6 7 8 9
from sklearn.neighbors import NearestNeighbors from matplotlib import pyplot as plt neighbors = NearestNeighbors(n_neighbors=4) neighbors_fit = neighbors.fit(dataset) distances, indices = neighbors_fit.kneighbors(dataset) distances = np.sort(distances, axis=0) distances = distances[:,1] plt.plot(distances)
- 그리고 그것의 팔꿈치가 뭐냐면
- 이렇게 생긴 거. 💪
- 즉 이 플랏 상 특정 지점으로 eps를 정하면 그것보다 k-dist가 적은 데이터포인트들은 클러스터로, 그보다 큰 데이터포인트들은 노이즈로 된다고 보면 되는데 그것이 급격하게 꺾여서 완만해지는 지점을 고르자는 것이다.
- 이렇게 생긴 거. 💪
작은 사족
오랜만에 무슨 글을 쓸까 하다가 수요가 있는 글을 써보기 위해 서치 콘솔을 참고했습니다. 서치 콘솔이나 GA는 붙여만 놓고 잘 보지 않게 되는데… 아무튼 이번에 보니 제 블로그에 스펙트럴 클러스터링 이해하기 라는 글을 통해 들어오는 분들이 많더라고요. 스펙트럴 클러스터링은 DBSCAN과 달리 수식이 좀 많이 필요하기 때문에 제가 처음 접했을 때 이게 대체 뭔 소리야 뭘 어떻게 한다는 거야? 라는 마음으로 열심히 공부하고 나서 작성한 글인데요. 그게 유입이 많다니 이참에 다른 클러스터링 기법도 다뤄 보았습니다. DBSCAN은 만만하고 익숙하다고 생각했지만 이렇게 자세히 찾아본 적은 또 없었던 것 같아서 좋았네요. 읽는 분들에게도 도움이 됐으면 좋겠습니다. 🙋♀️