Data Drift 발견하기
머신러닝 모델에서 Data Drift가 무엇이며 어떻게 발견하는지에 대한 글입니다.
Drift란 무엇인가
그리스의 철학자 헤라클레이토스는 “같은 강물에 두 번 발을 담글 수 없다”라는 말을 남겼다고 합니다. 강물이 끊임없이 흐르기 때문에 어떤 사람이 똑같은 자리에 서서 두번째로 발을 넣는다 한들 그건 처음과 같은 강물이 아니라는 뜻이죠. 마찬가지로 현실 세계의 데이터도 끊임없이 변화합니다. 일반적으로 ML 모델을 프로덕션 단계로 보내기 전에 우리가 원하는 수준의 성능을 보이는지를 확실히 하고 넘어가지만, 문제는 그 이후에 데이터가 변할 가능성이 크다는 것이고, 대부분의 경우 변한다는 것입니다. 모델은 적용되는 그 순간부터 학습에 사용했던 데이터와 다른 데이터를 맞닥뜨리게 됩니다. 운이 좋다면 한동안은 잘 돌아가겠지만 시간이 더 지나면 높은 확률로 테스트 결과와는 다른 성능을 보이게 될 겁니다.
한 문장으로 짚고 넘어가면, 오늘 이 글에서 다룰 것은
데이터나 변수 간 관계 변화로 인한 프로덕션 모델의 성능 저하
라는 현상(Drift)입니다.
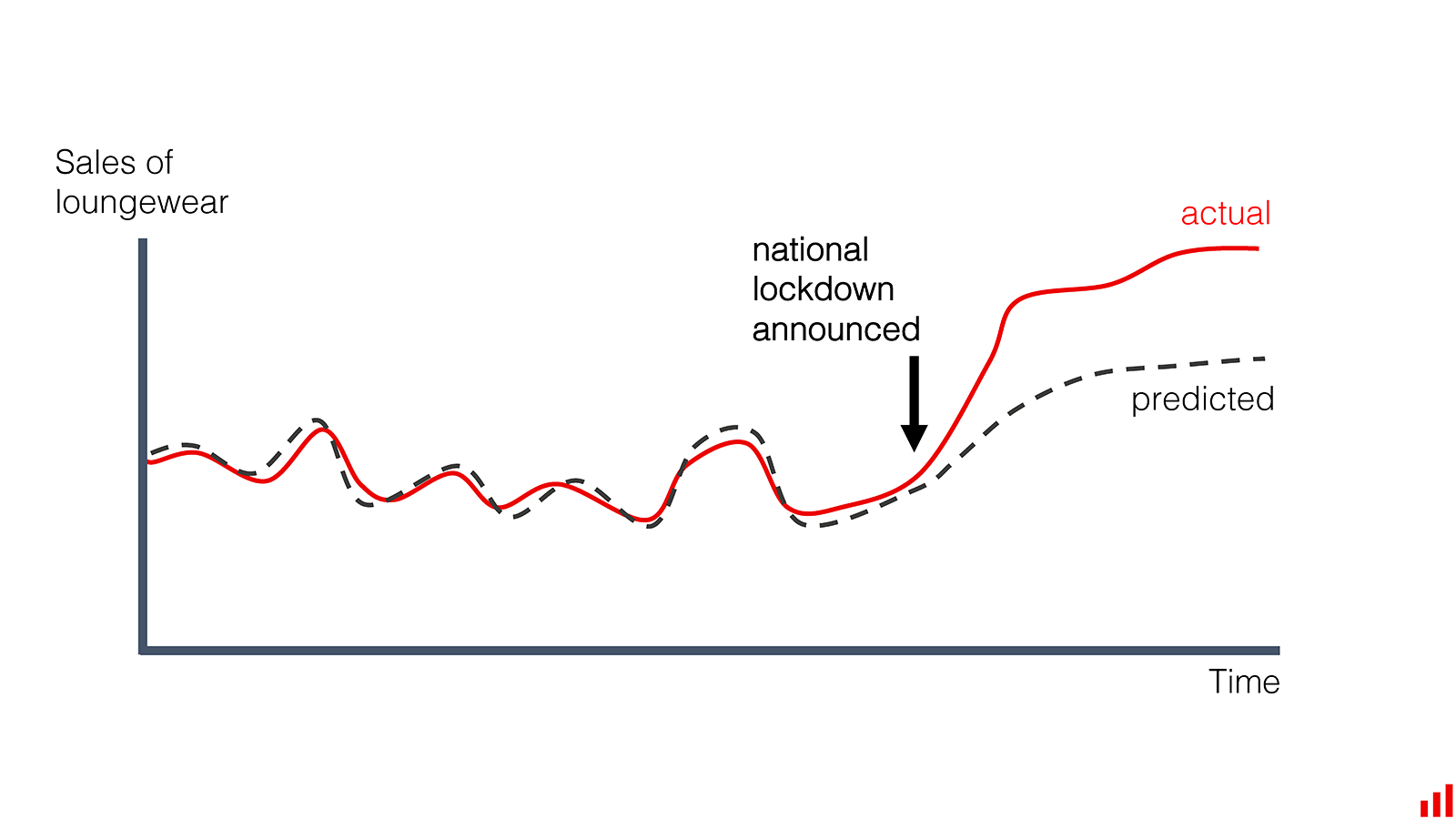특정 사건으로 인해 사람들의 소비가 변화하면서 모델의 예측과 동떨어지게 됨 - 이미지 출처
이런 현상을 부르는 말은 뭐 model drift, concept drift, data drift 등으로 다양한 것 같습니다. 보통 데이터의 통계적인 특성이 변화하는 걸 일반적인 용어로 concept drift로 일컫는 것 같고, 아래에서 조금 더 자세히 다루겠지만 여러 개념으로 쪼개서 각각 다른 이름을 붙이기도 하는 듯합니다.
아무튼 이 글은 주로 drift가 발생했을 때 이를 발견할 수 있는 방법들을 다룰 건데요. 들어가기 전에 그걸 왜 발견해야 돼? 라는 생각을 할 수도 있겠습니다. 어차피 필연적으로 데이터가 변화하는 거라면 그냥 최신 데이터에 맞게 계속 모델을 다시 학습시키면 되는 거 아닌가?
물론 그냥 때마다 모델 다시 학습시키도 가능한 해결책이 될 수 있겠습니다. 하지만 모델 학습이나 데이터 획득에 큰 비용이 드는 경우, 시간이 지났다는 이유만으로 그 리소스를 들여서 무조건 재학습을 하는 것은 비효율적인 선택이라고 할 수 있습니다. 적절한 주기를 찾는 것도 하나의 큰 과제일 수 있겠고요.
또한 모델과 상호작용하여 데이터의 변화가 일어났다면, 그 변화의 양상을 전혀 모르는 채로 단순히 처음 모델링을 할 때의 프로세스를 처음부터 다시 거치는 것만으로는 문제가 해결되지 않거나, 헤매게 될 수도 있습니다. 예를 들어 사기 거래 여부를 분류하는 모델을 만들었고, 해당 모델이 제법 성능이 좋아서 그 분류 결과를 통해 사기꾼들이 거래하지 못하도록 조치를 취했다고 칩시다. 이런 영역의 문제점은 나쁜 사람들은 보통 즉각적으로 반응을 한다는 것입니다. 만약 모델이 사기라고 분류한 케이스 중 대다수가 백 만원 이상의 고액 결제건이었다면, 앞으로 사기를 치고 싶은 사람들은 안 걸리게 십 만원씩 쪼개서 거래를 해볼까? 라고 생각할 수 있습니다. 우리가 만약 그 데이터(건당 결제금액)의 분포 변화를 감지하고 어떻게 바뀌었는지 분석할 수 없다면 모델을 개선하는 데 어려움이 있겠죠 (사실 제가 맨날 겪는 일..🥲).
결론적으로 데이터의 변화가 어떤 변수에서 어떤 방향으로 일어났는지 발견하고, 그게 현재 모델의 성능에 어떤 방식으로 영향을 끼치고 있는지 파악해야 보다 효과적이면서도 비용을 낭비하지 않는 해결책을 찾아낼 수 있습니다.
Drift의 종류
크게 2가지 기준으로 구분해볼 수 있습니다.
- 개념적인 구분
- Drift를 간단한 공식으로 나타낸다면, 어떤 방식으로든 타겟 변수(y)와 사용한 피쳐(X)의 관계의 분포가 변화한다는 것을 뜻함
- 즉 결합확률분포의 변화 : $P_{t}(X,y)!= P_{t+}(X,y)$
- 이걸 쪼개보면,
- $P(X)$의 변화 ( Covariate drift, Data drift ) : 인풋 피쳐의 분포가 변하는 경우
- ex) 이탈율 예측을 하는데 예전에는 2-30대가 주로 이용하던 상품인데 트렌드의 변화 등으로 인해 요즘은 3-40대로 타겟 고객이 변화했을 때. 인풋 중 하나인 ‘나이’의 분포가 변화함
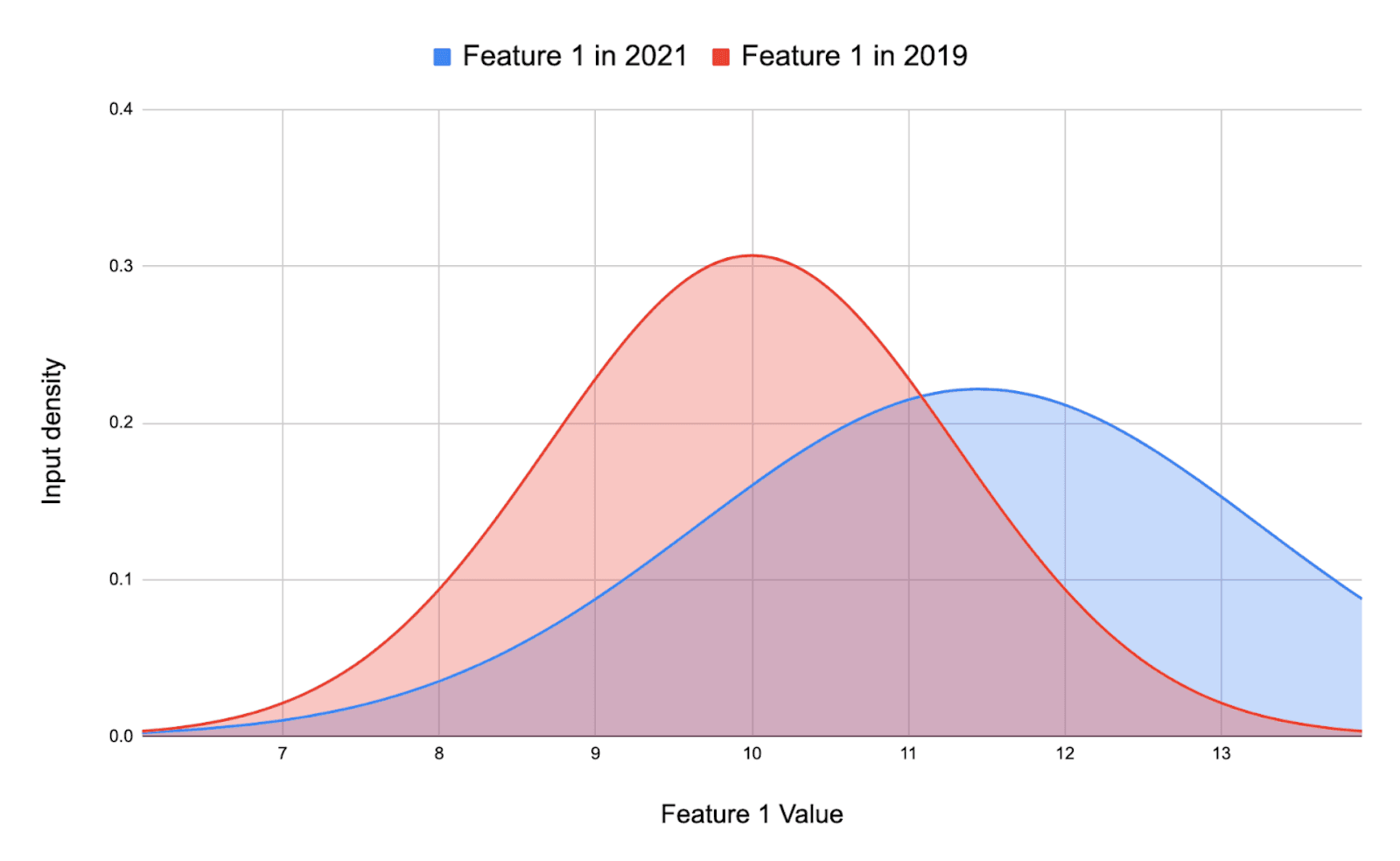이미지 출처
- $P(y)$ 의 변화 ( Label drift, Prior probability shift ): 타겟 변수의 분포가 변하는 경우 사기 탐지를 한다면
- $P(y|X)$ 의 변화 (Concept drift, Conditional change, Posterior class shift) : 인풋과 타겟 변수의 관계가 변하는 경우 - 가장 발견하고 규명하기 어려운 종류의 변화
이미지 출처
- $P(X)$의 변화 ( Covariate drift, Data drift ) : 인풋 피쳐의 분포가 변하는 경우
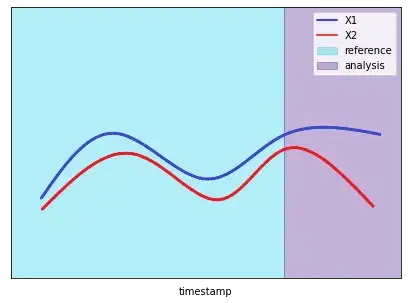
- 이런 것들을 개념적으로 쪼개 보는 이유는 다음과 같이 데이터의 변화가 반드시 모델의 결정경계를 건드리지는 않는 경우도 있기 때문!
이미지 출처
- Drift를 간단한 공식으로 나타낸다면, 어떤 방식으로든 타겟 변수(y)와 사용한 피쳐(X)의 관계의 분포가 변화한다는 것을 뜻함
- 양상에 따른 구분
- 다음 그림을 보면 쉽게 이해됨
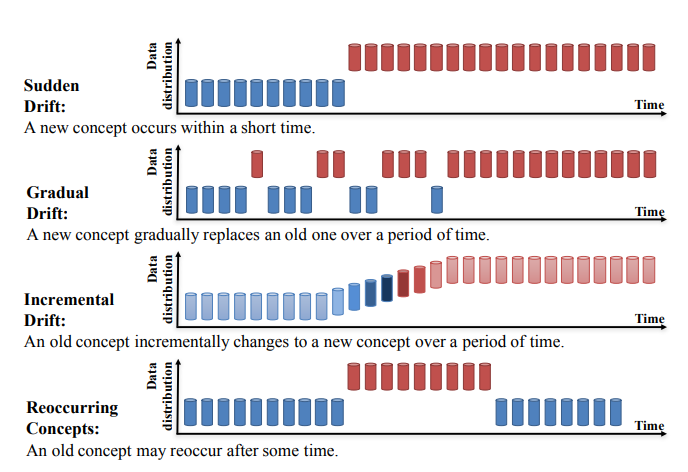이미지 출처
- 다음 그림을 보면 쉽게 이해됨
Drift가 발생하는 이유?
다음은 흔히 언급되는 drift를 유발하는 원인들입니다.
- 학습 데이터 자체의 샘플링 편향이 있어서
- 잘못된 데이터 파이프라인이나 버그 등 테크니컬한 이슈가 있어서
- 명시적으로 사용한 피쳐가 아닌 숨겨진 변수가 변해서
- ex) 놀이공원에 온 사람의 수를 예측하는데 날씨나 요일, 휴일 여부를 사용했는데 전반적으로 경기가 안 좋아진다면?
- 그냥 외부 환경 자체가 바뀌어서
- 모델 자체의 영향, 숨겨진 피드백 루프가 있어서
- 공격에 대응하는 목적의 분류 문제(스팸 필터링, 네트워크 침입, 사기 탐지)에서 공격자가 모델에서 1로 분류되는 걸 피하기 위해 명확히 노력하는 경우
- 마케팅 캠페인처럼 사용자에게 직접 영향을 주는 경우
- ex) 이탈 예측을 했는데 이탈할 고객에게 쿠폰을 줘서 이탈을 안 했다면?
- 도메인적인 변화
- ex) 인플레이션이 오면 소득이나 물가 자체가 가지는 의미가 변경됨
어떻게 발견하는가
기본적으로는 비교 대상인 분포 2개의 데이터가 있어야 합니다. 즉 내가 비교하려고 하는 분포(Tested distribution)이 있고, 그게 뭐에 비해서 달라진 것이냐? 를 보는 근거 분포(Reference distribution)를 나누어 볼 수 있는데요. 보통 tested distribution이 아마 더 최신의 데이터일 것이고, reference distribution은 보다 이전의 데이터이거나(ex.전주 동일 요일) 학습에 사용했던 데이터 등 과거의 데이터를 의미합니다.
시간이 흐름에 따라 매번 이전의 데이터와 비교를 하겠다면 sliding window로 일정 시간 텀마다 비교할 수 있겠죠? 그렇다면 그 주기를 정하는 것도 중요한 문제입니다(ex. 1분 전? 어제? 전주? 전달?). 타이밍을 줄일수록 빠르게 drift를 발견할 수 있겠지만 노이즈도 많아지기 때문입니다. 이 가게에 원래 금요일 밤에는 30대 직장인이 많이 방문하는데, 어제(목요일 밤)과 분포가 다르다고 문제가 생겼다고 볼 수는 없듯이요.
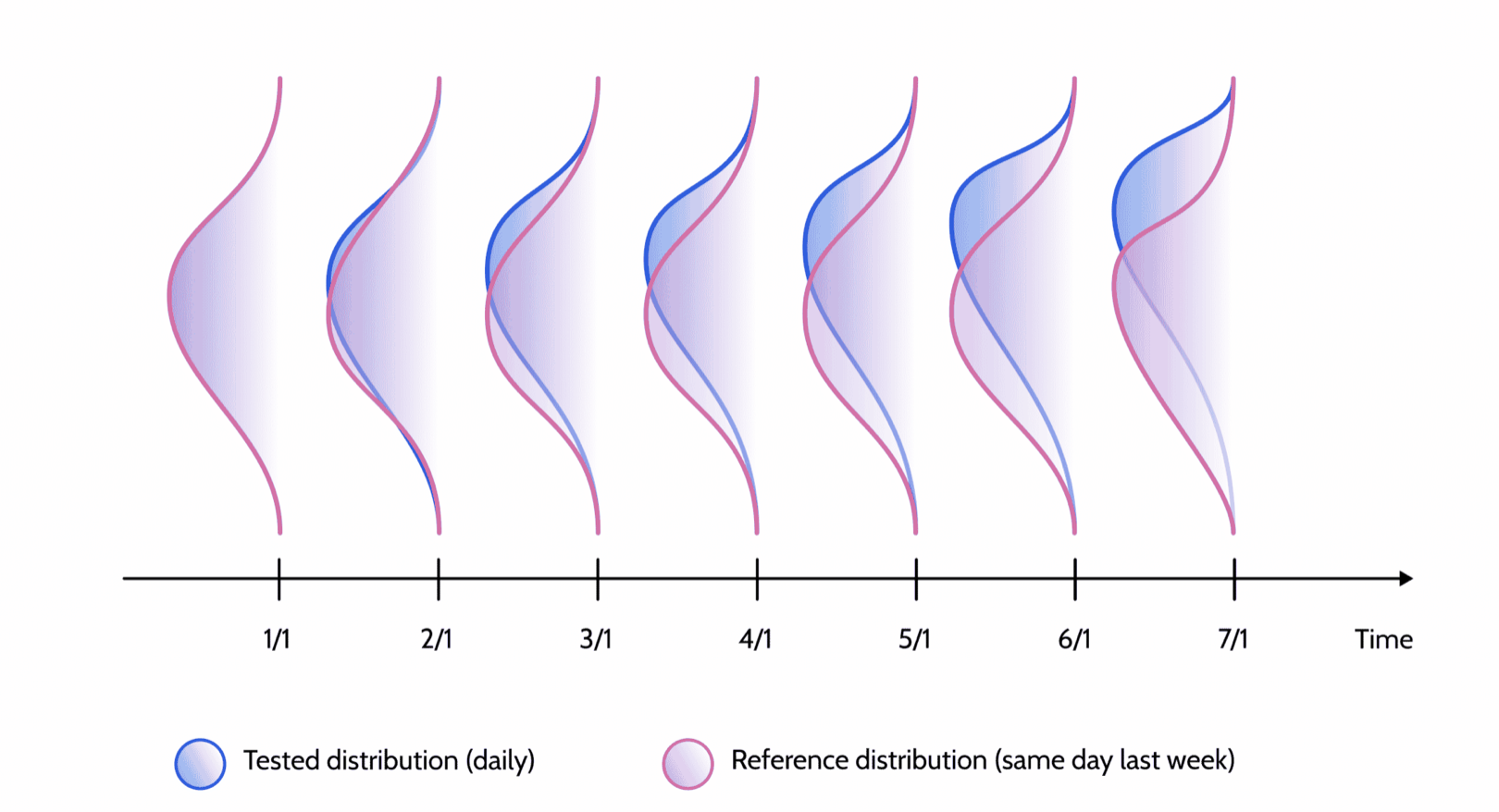한달에 한번, 전주의 같은 요일과 비교하기 - 이미지 출처
어쨌든 이런 것들을 정했다고 치고, 이제 일정 주기마다 데이터를 비교해서 drift가 발생할 경우 나에게 얼럿을 주는 시스템을 상상해 봅시다. 이런 시스템이라면 결국 drift의 정도를 하나의 단일한 값으로 나타내주고 그 값에 대해 이 정도를 넘으면 경고다! 라는 임계값(threshold)를 정할 필요가 있겠죠.
분포 간 통계적 차이를 계산해보자
간단한 접근으로, 각각의 피쳐에 대해 단변량으로 접근해서 하나하나 모니터링할 수 있겠습니다. 이때는 각각의 drift 정도를 수치화한 다음 하나의 값으로 집계하고, 이때 피쳐 중요도에 따라 가중치를 둬도 좋을 듯합니다.
따라서 두 개의 데이터를 놓고 그 분포가 얼마나 떨어져 있는지 거리를 수치화하는 다음과 같은 방법들이 필요하겠습니다.
- Kolmogorov-Smirnov Test (K-S Test)
- 보통 정규성 검정 방법으로 많이 알려져 있지만 원하는 분포-정규분포(1-sample) 간 검정 뿐 아니라 2개의 데이터가 같은 분포에서 나왔는지도 검정이 가능함(2-sample)
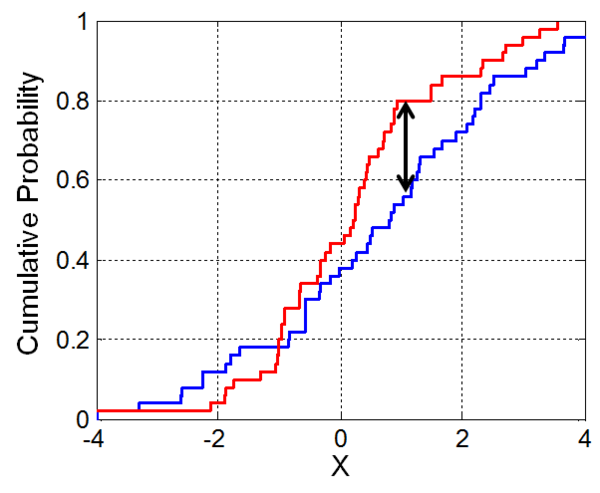이미지 출처 - 누적분포함수를 그림으로 그려보면 저 검은색 선인 둘 사이의 거리 D를 통계량으로 테스트함
- $D_{n,m} = \sup \mid F_{1,n}(x) - F_{2,m}(x) \mid$
- 쉽게 쓰면 그냥 두 누적분포의 최대 차이라는 뜻
- 영가설은 두 데이터의 분포 간 차이가 없다 (p값이 유의수준 이하일 경우 기각되어 차이가 있다)
- $D_{n,m} = \sup \mid F_{1,n}(x) - F_{2,m}(x) \mid$
from scipy.stats import ks_2samp로 쓸 수 있음
- 보통 정규성 검정 방법으로 많이 알려져 있지만 원하는 분포-정규분포(1-sample) 간 검정 뿐 아니라 2개의 데이터가 같은 분포에서 나왔는지도 검정이 가능함(2-sample)
- PSI (population stability Index)
- $\text{PSI} = \sum((\text{Tested} - \text{Reference}) \times \ln (\frac{\text{Tested}}{\text{Reference}}))$
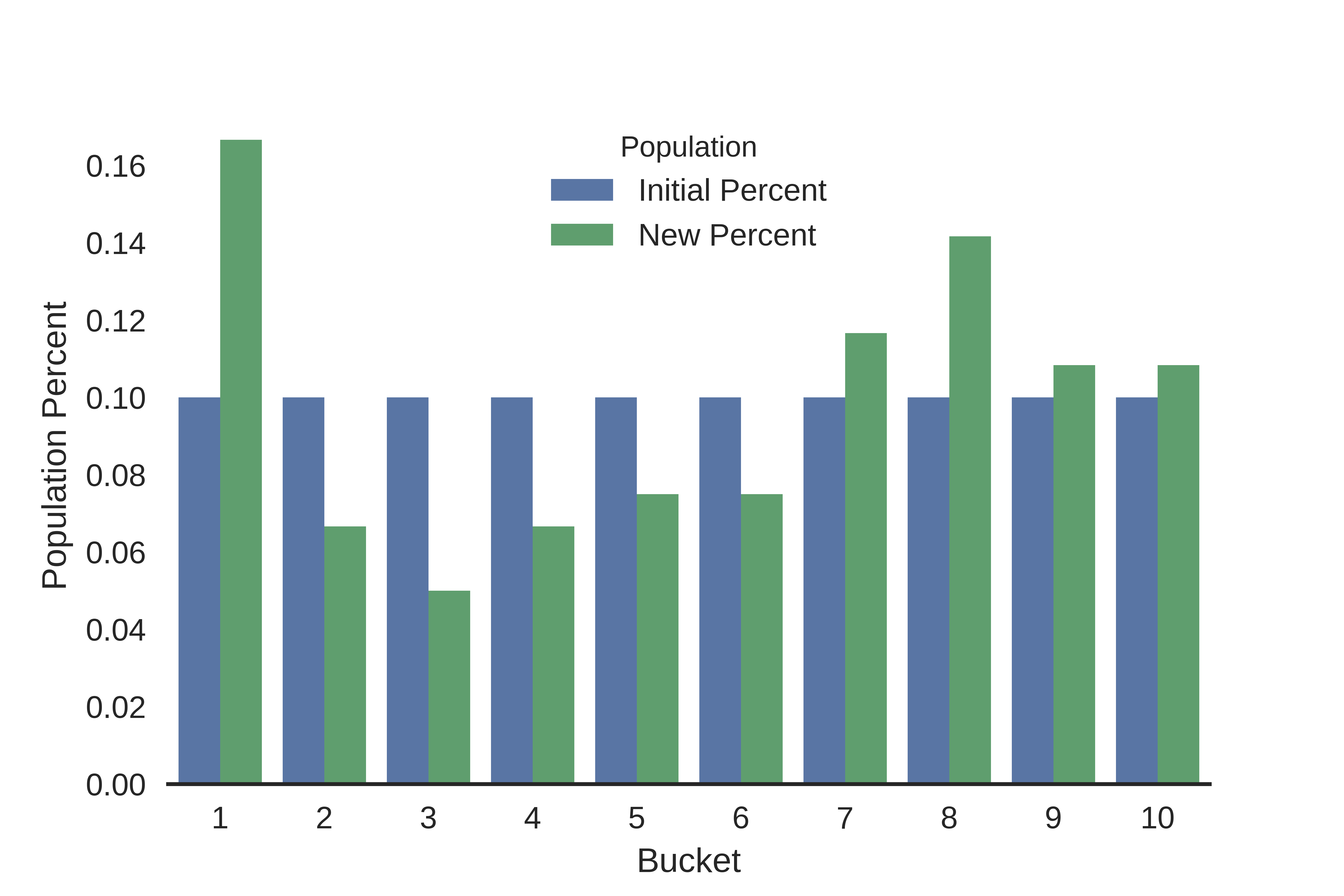
- 간단한 예시 - 지난주에는 페퍼로니 피자 주문 고객이 전체의 60% 였는데 이번주는 30% 라고 한다면 위 공식에 tested = 30%, reference = 60%로 계산해볼 수 있고 이걸 모든 메뉴에 대해 계산해서 합하면 됨
이미지 출처
- 간단한 예시 - 지난주에는 페퍼로니 피자 주문 고객이 전체의 60% 였는데 이번주는 30% 라고 한다면 위 공식에 tested = 30%, reference = 60%로 계산해볼 수 있고 이걸 모든 메뉴에 대해 계산해서 합하면 됨
- 카테고리컬한 분포 또는 bin으로 나눈 데이터에 쓰기 편한 지표고 구현도 그냥 하면 될 듯. 다음과 같이 알려진 공식도 있음
- $\text{PSI} < 0.1$ : 변화 없다
- $\text{PSI} < 0.2$ : 약간 변화했다
- $\text{PSI} \ge 0.2$ : 심하다 너 경고
- $\text{PSI} = \sum((\text{Tested} - \text{Reference}) \times \ln (\frac{\text{Tested}}{\text{Reference}}))$
- Jensen-Shannon Diveregence (JS Divergence)
- Kullback-Leibler Divergence (KL Divergence)의 대칭 버전
- KL Divergence의 아이디어는 한 분포를 다른 분포로 근사할 경우에 얼마나 정보 손실이 발생하느냐? (즉 두 분포가 매우 비슷하다면 손실이 별로 없을 것이고, 다르다면 많이 발생할 것이고)
- $D_{KL}(p\mid q) = \sum {p(x_i)\cdot (\log p(x_i)-\log q(x_i))}$
- 두 분포 차이에 대한 기대값
- 이걸 쪼개면
p 입장에서 q에 대한 크로스 엔트로피 - p의 엔트로피
- 다만 $D_{KL}$ 함수는 거리 함수로 볼 수 없는데, 대칭이 아니어서 = A와 B 의 아웃풋과 B와 A의 아웃풋이 달라서 (A를 B로 근사하느냐 B를 A로 근사하느냐)
- KL Divergence의 아이디어는 한 분포를 다른 분포로 근사할 경우에 얼마나 정보 손실이 발생하느냐? (즉 두 분포가 매우 비슷하다면 손실이 별로 없을 것이고, 다르다면 많이 발생할 것이고)
- JSD는 다음과 같이 KLD를 양쪽으로(각 분포를 두 분포의 평균으로 근사) 구한 뒤 평균내서 하나의 값으로 만들어준 것
- $\text{JSD}(p,q) = \frac{1}{2}D_{KL}(p \mid \frac{p+q}{2}) + \frac{1}{2}D_{KL}(q \mid \frac{p+q}{2})$
rom scipy.spatial.distance import jensenshannon로 쓸 수 있음
- Kullback-Leibler Divergence (KL Divergence)의 대칭 버전
다만 이런 단변량적 시야에는 한계가 몇 가지 있습니다.
- 피쳐가 엄-청 많다면 계속 이걸 하나하나 비교하는 로직을 돌리는 게 낭비 아닐까?
- 상관관계가 높은 변수들은 한꺼번에 drift될 수 있는데 이게 최종적인 drift 점수에 redundant하게 반영되지 않을까?
- 다변량적으로(변수가 상호작용하여) 발생하는 drift는 놓치지 않을까?
모델의 오차를 모니터링하자
단변량 접근 말고 통째로 모델 단위로 접근하는 방법을 생각해 봅시다. 모델 학습에 비용이 크게 들지 않는 상황이라면 비교 대상인 두 개의 데이터를 놓고, 따로 모델을 학습시켜서 얼마나 두 개의 모델이 동의하지 않는지(성능이든 피쳐 중요도든)를 수치화해볼 수 있습니다. 하지만 모델 재학습을 최대한 효율적으로 하려고 drift를 사전에 발견하려는 게 아닌가? 싶으니 이건 그렇게 좋은 방법이 아닐 수도 있겠어요.
아니면 시간의 흐름에 따라 모델의 틀림 자체를 모니터링할 수도 있겠죠. 다음 방법들은 scikit-multiflow 로 쉽게 써볼 수 있습니다.
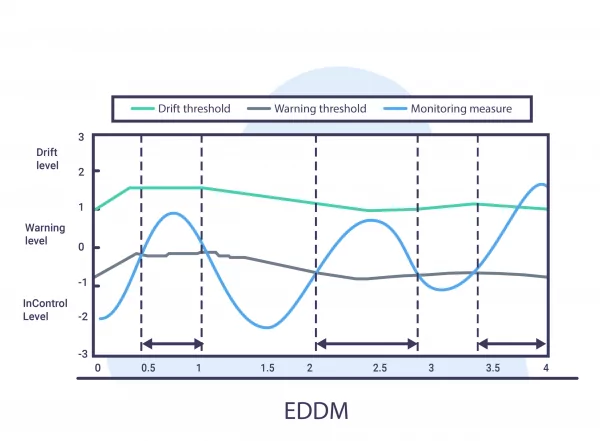오차 모니터링 예시 - 이미지 출처
- DDM (Drift Detection Method)
- 모델이 틀린다/틀리지 않는다를 binomial 변수로 봄
- 이항분포를 생각해보자 - $n$번 맞힐 때 독립적으로 $p$의 확률로 틀리거나, 틀리지 않는
- $p_t$ : 테스트 시점의 오차율(error rate)
- 즉 틀림의 기댓값과 편차를 이항분포의 공식에 따라 정의할 수 있다는 뜻
- $\mu = np_t$
- $\sigma = \sqrt{\frac{p_t(1-p_t)}{n}}$
- 그러면 다음과 같이
지금까지 기록된 오차율 최소값 + 그때 k*편차와 비교했을 때테스트 시점의 오차율 + 편차가 커져버릴 때 알람을 주는 임계값 설정이 가능- 경고: $p_t + \sigma_t \ge p_{min} + 2\sigma_{min}$
- 찐 알람: $p_t + \sigma_t \ge p_{min} + 3\sigma_{min}$
- 모델이 틀린다/틀리지 않는다를 binomial 변수로 봄
- EDDM (Early Drift Detection Method)
- 접근은 DDM과 유사하나 DDM에 비해 점진적인 drift를 더 잘 잡아낼 수 있다고 함
- 알람을 주는 기준은
테스트 오차율+그때 2*편차가오차율 최고값+그때 2*편차와 매우 가까워질 때- 경고: $\frac{p_t + 2\sigma_t}{p_{max}+2\sigma_{max}}< \alpha$
- 찐 알람: $\frac{p_t + 2\sigma_t}{p_{max}+2\sigma_{max}}< \beta$
- $\alpha$, $\beta$ 는 사용자가 정하는 임계치고, 보통 $\alpha$ 0.95, $\beta$ 0.9가 보통 디폴트
- (모든 임계치가 그렇듯 빠르게 drift를 알리고 어느 정도의 false alarm을 감수할 것이냐의 trade-off는 당연히 존재함)
- $\alpha$, $\beta$ 는 사용자가 정하는 임계치고, 보통 $\alpha$ 0.95, $\beta$ 0.9가 보통 디폴트
- PHT (Page-Hinkley Test)
- 기본적으로 지금 값이 이전 값들에서 현저하게 떨어진 값일 경우 알람을 주는 로직
- 단방향(커지는 것만 체크)이지만, 모델 drift를 발견하는 목적으로 오차가 커지는 걸 탐지하는 데 이 테스트를 사용한다면 굳이 양방향일 필요 없을 듯
- CUSUM Test에 기반
- $g_0 = 0$ 이고, $g_t =$ $\max(0, g_{t-1} + (z_t -v))$
- $g$는 모델의 아웃풋(예를 들어 오차)를 뜻함
- $z$는 지금까지 시퀀스를 기반으로 계산된 기대값, 편차를 사용한 표준화값 ($z =(x-\mu)/\sigma$)
- $v$는 설정되어야 하는 파라미터인데, 보통 발견해야 하는 수준의 변화의 1/2 정도를 설정한다고 함 (단 표준편차 단위임을 유의)
- $g_t > h$이면 알람을 주고 $g_t=0$ 으로 리셋한다!
- 이때 $h$는 설정해야 하는 임계치 파라미터인데, 보통 용인 가능한 false alarm 비율이 $\delta$ 라고 치면 $\ln(1/\delta)$ 로 설정한다고 함
- $g_0 = 0$ 이고, $g_t =$ $\max(0, g_{t-1} + (z_t -v))$
- CUSUM은 memoryless하므로(직전 값만 고려) 이를 보완한 것이 PH Test
- $g_0 = 0$ 이고, $g_t =$ $g_{t-1} + (z_t -v)$, $G_t = \min(g_t, G_{t-1})$
- $G_t$는 $t$까지 가장 작은 값이 되도록 설정하므로 전체 앞선 시퀀스를 다 고려할 수 있음
- $g_t-G_t > h$ 이면 알람을 주고 $g_t = 0$으로 리셋한다!
- $g_0 = 0$ 이고, $g_t =$ $g_{t-1} + (z_t -v)$, $G_t = \min(g_t, G_{t-1})$
- 기본적으로 지금 값이 이전 값들에서 현저하게 떨어진 값일 경우 알람을 주는 로직
다만, 이렇게 모델 단위로 drift를 발견해도, 결국 뭐가 어떻게 문제인지 알아내고 싶다면 각각의 피쳐로 drill down해서 보고 분포의 차이를 명확히 검증해 봐야 하는 경우가 많을 것 같다는 생각도 드네요.
차원 축소 후 데이터를 복구해보자
또다른 아이디어로는 데이터셋을 PCA 등으로 차원 축소한 다음 복구를 해볼 수도 있습니다. 데이터가 어떻게든 많이 바뀌었다면(PCA가 배운 분산의 형태에서 많이 떨어지게 되었다면) 복구 데이터의 오차가 커질 것이라고 가정하여, 원래 데이터포인트와 복구된 데이터 간의 유클리디언 거리를 drift 점수로 쓰는 것입니다.
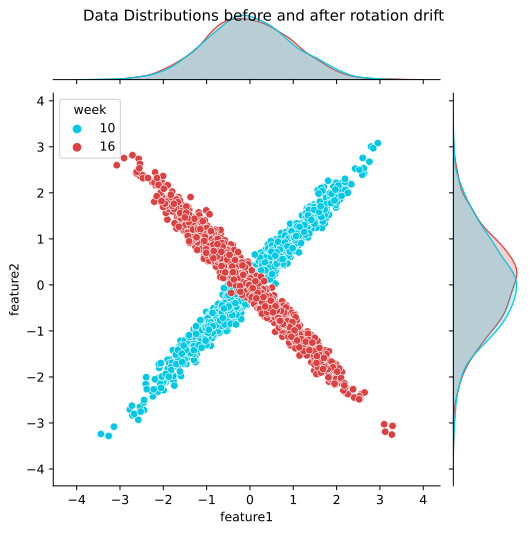
모델 성능 예측과 모니터링에 쓰이는 NannyML 패키지 공식 문서에 PCA를 사용한 방법으로 다변량 drift를 발견한 예시가 있어서 가져와봤습니다.
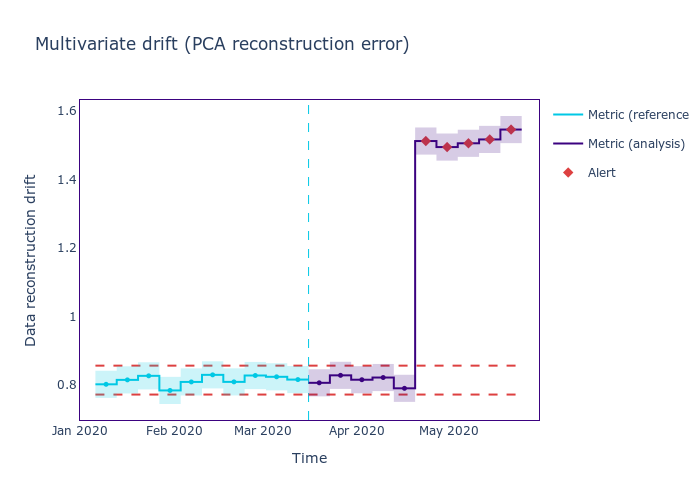
별로 현실적인 예시는 아니지만 이런 식으로 두 개의 피쳐의 관계가 휙 돌아가(?) 버렸다면 분명 drift가 일어난 건 맞는데, 위와 우측에 그려진 각각의 단변량 분포를 보면 각각의 피쳐 내에서는 분포가 바뀐 것처럼 보이지가 않습니다. 이럴 때 앞서 언급한 PCA 방법을 쓰면, 다음과 같이 복구 오차가 증가하는 것을 볼 수 있습니다.
