인과 추론 1. 상관은 인과가 아닌데
아닌데… 그럼 인과는 뭐야?
이야기의 시작은 기초적인 통계학 수업을 들어 본 분들이라면 많이들 공감할 만한 것으로 하겠습니다. 바로 “상관은 인과가 아니다”라는 통계학 첫 시간에 가장 많이 등장하는 말인데요. 이 말을 간단하게 보여주는 예시들은 차고 넘치지만, 몇 년 전 제 경험을 가져와 볼게요.
제가 처음으로 들은 통계학 수업에서 강의하시던 분은 “어느 나라에서 아이스크림이 많이 팔릴수록 익사로 사망하는 사람이 늘어나더라”를 예시로 가져오셨습니다. 이건 그냥 데이터입니다. 우리가 흔히 아는 수치(ex. 피어슨의 상관계수)로 보여줄 수 있겠죠. p<0.05 수준에서 유의미하게 0.4의 상관!이라고 칩시다. 그러나 익사 사망률과 아이스크림 판매량 사이에 어떤 정적인 상관이 존재한다고 해서 우리는 아이스크림에 뭔가 치명적인 물질이 들어서 그걸 먹으면 갑자기 물에 빠져 죽는다는 결론을 내릴 수 없습니다. 반대로 사람들을 물에 빠뜨려 죽일수록 아이스크림이 잘 팔릴 거라고 기대할 수도 없죠. 두 변수 사이에 있는 건 상관이지 인과가 아니니까요.
조금 더 생각해보면 우리는 상식적으로 ‘더위’라는 공통 변인이 저 현상에 영향을 주고 있다는 걸 알 수 있습니다. ‘상식적으로는’요. 하지만 실제로 “더워서 → 아이스크림이 잘 팔린다” 혹은 “더워서 → 사람들이 물놀이를 많이 해서 → 잘 빠져 죽는다”는 결론을 내리기까지는 굉장히 많은 노력이 들어갑니다. 인과는 우리가 일상적으로 굉장히 많이 사용하는 사고방식임에도 불구하고(예를 들어 전 방금도 “아, 어제 이상한 자세로 자서 목이 아파.”라고 말했습니다.) 어떨 때 주어진 사실만으로 인과를 증명할 수 있는지, 증명이 가능하긴 한 건지에 대해서 통계학은 물론 철학계에서부터 길고 긴 논쟁이 있었습니다. 현실 세계에서 변수가 많아질수록 인과 관계는 점점 더 불투명해집니다(진짜 제가 이상하게 잤기 때문일까요? 아침에 옷을 입다가 삐끗한 건 아닐까요? 아니면 원래 제 근육통이 만성 질환이라면?). 한 마디로, 상관을 보이는 것은 쉽지만 인과는 아닙니다. 그래서 통계학에서는 아주 오랫동안 “상관은 인과가 아니다”를 주문처럼 외우면서 인과 논의를 터부시해왔던 것입니다.
물론 통계학이 금지하지 않은 간단한 해법이 하나 있습니다. 바로 실험을 하는 겁니다. 완벽하게 무선화된 표본을 선정하고, 통제조건과 실험조건을 나누어 다른 처치를 부여한 다음 어떻게 되는지 보는 것이죠. 하지만 많은 경우 실험은 비용이 너무 많이 들거나 아예 가능한 옵션이 아닙니다.
- 윤리적으로 안 되니까 ex. 어린 나이에 흡연을 시작하면 일찍 죽을까?
- 원인이 되는 변수를 내가 통제할 수 없으니까 ex. 갑자기 더워지면 아이스크림이 얼마나 팔릴까?
- 데이터 자체가 과거의 것이라서
그리고 실험을 하지 않고 우리가 그냥 접하는 수많은 데이터(실험한 게 아니라는 측면에서는 관찰 데이터라 할 수 있죠)에서 인과를 보이려면, 일반적인 통계적 방법론이 아닌 다른 툴이 필요합니다.
인과 추론, 왜 할까?
‘왜’는 우리가 일상적으로, 그리고 각종 과학과 사회과학과 비즈니스에서 가장 자주 묻는 질문입니다. 왜 주가가 올랐을까? 짠 걸 많이 먹으면 심장병이 생기나? 간판을 바꿔 달면 손님이 더 많이 올까? ‘왜’ 질문은 끝이 없습니다.
하지만 어떤 사람들은 인과가 중요하지 않다고 말하기도 합니다. 특히 머신 러닝이 고도로 발달하면서 그런 생각이 이전보다 대중적인 의견이 되기도 했죠. 인과 없이도 충분한 재료(방대한 양의 데이터! 수만 개의 피쳐들!)만 있다면 우리의 모델은 수천 종의 동식물 사진을 분리해낼 수 있고, 몰랐던 이상 세포를 찾아내고, 지역마다 범죄율도 예측하고, … 굳이 다 나열하지 않겠습니다. 아무튼 상관만으로도 예전에는 상상도 할 수 없었던 일들을 척척 하잖아요? 그런데 왜 굳이 다른 툴까지 써가면서 인과를 증명해야 할까요?
우선 우리는 데이터를 분석함으로써 얻은 결과를 (그 분석 과정에 ‘인과’는 전혀 포함되어 있지 않음에도 불구하고) 인과적으로 사용하고자 할 때가 많습니다. 즉, 인과에 기반한 결정을 내리고 행동을 하고 싶어 합니다. 일반적으로 우리는 상관만을 기반으로 어떤 일이 일어날지 예측하고 실행하지 않습니다. 인과를 판단하기 어려울 때는 그렇게 하지만, 우리의 사고과정의 핵심적인 매커니즘은 아니에요. (그래서 진정한 AI는 인과적인 판단과 추론을 할 수 있어야 한다는 주장이 나오기도 합니다.) 분석 결과를 사용하기 위해서는 우리의 사고가 납득해야 하는 경우가 많습니다. ‘왠진 잘 모르겠지만 X가 올라가니 Y도 올라간다’는 인사이트를 기반으로, 그게 어떤 방식으로 작동하는지도 모르면서 그럼 X를 늘리자! 하는 의사결정을 하는 것은 쉽지 않은 일이죠.
제가 맨 처음에 든 예시에서도, 만약 아이스크림을 파는 사람이라면 아이스크림을 많이 팔고 싶으니까 무엇이 매출 상승의 원인인지 알고 싶을 것입니다. 어디서 팔면, 어떻게 팔면, 무슨 종류를 팔면 잘 될까? 그러나 이런 질문에 대한 대답으로 저런 상관은 아무 도움이 안 되거나 틀린 선택을 하게 하죠. 물론 일반적으로는 저 데이터를 보고 사람을 물에 빠뜨려 죽여야 한다고 생각하진 않을 테지만, 실제 데이터에서 변수가 많아지고 그 관계가 복잡해지면 우리는 잘못된 상관으로 인해 잘못된 판단을 할 가능성이 높아집니다(널리 알려진 심슨의 역설이 그 예시 중 하나입니다.) 혹은 아예 판단이 결정으로 이어지기 어렵습니다.
물론 잘 만들어진 상관 기반의 예측 모델은 많은 과학적 질문에 대답할 수 있고 비즈니스 결정을 훌륭하게 도와줍니다. 그러나 X가 주어졌을 때 Y를 추정하는 능력을 최대화하는 것을 목적으로 작동하는 예측 모델과는 달리 인과 추론은 우리가 X를 바꾸면, 즉 실제 행동하면 Y가 어떻게 바뀔지에 관심을 가집니다. X를 실제로 바꿀 수 없을 때나 바꾸기 전에 미리 답을 얻을 수 있는 방법을 추구하는 것이죠.
안타깝게도 통계학은 ‘상관은 인과가 아니다’라는 이 상식 수준의 관찰 결과를 지나치게 숭배해왔다. 저 말은 상관이 인과가 아니라는 사실만 알려줄 뿐, 정작 인과가 무엇인지는 알려주지 않는다. 통계학을 배우는 학생들에게 X가 Y의 원인이라고 말하는 일은 금지되어 있다. X와 Y가 “관련이 있다” 혹은 “연관되었다”고만 말하는 게 허용된다. - Judea Pearl, Book of Why
인과 추론, 뭘까?
다시, 상관은 인과가 아닙니다(이제 지겹죠?). 그리고 인과는 알아낼 수만 있다면 우리에게 도움이 될 겁니다. 그럼 대체 무엇이 인과인가요?
우선 제가 위에 인용한 것은 이 인과 추론 분야의 유명한 Judea Pearl 이라는 분이 누구나 쉽게 읽을 수 있는 책으로 인과 추론에 대해 저술한 <인과에 대하여(The Book of why)>라는 책입니다. 인과가 무엇인지 알기 위해 이 Pearl의 다른 글에서 등장한 일명 인과의 3단계를 살펴봅시다. 인과를 계산 혹은 증명 가능하게 정의하는 것은 이후에 각 프레임워크마다 달라질 수 있지만 이 3단계는 전반적인 개념 파악에는 도움이 됩니다. 차례대로 살펴보면:
- 연관 (Association) = $P(y \mid \text{see}(x))$ : 관찰된 X가, 즉 X를 보는 것이 Y에 대한 내 믿음을 바꿀까? - 통계적 관계, 대부분의 머신 러닝 시스템이 동작하는 수준
- 개입 (Intervention) = $P(y \mid \text{do}(x))$: X를 하면 Y에 변화가 일어날까? - 강화학습 시스템이 정의된 환경 안에서 동작하는 수준
- 반사실 (Counterfactuals) = $P(y_x \mid x’,y’)$ : X를 안 했더라면 그래도 Y가 일어났을까?
이것이 ‘단계’인 이유는 i 단계의 질문은 i 혹은 그보다 더 높은 단계의 질문에 대한 답을 알고 있을 때만 답변 가능하기 때문입니다(i=1,2,3). 결국 인과 추론의 최종적인 단계는 Counterfactual, 일종의 상상입니다. 제가 잠을 이상한 자세로 잔 게 오늘 목이 결리는 것의 원인이라고 말하려면, 그냥 어젯밤으로 시간여행을 해서 이번엔 똑바른 자세로 자 보면 됩니다. 물론 가능한 일은 아니죠. 그래서 추론이 필요한 것이고요.
인과 추론, 어떻게 할까?
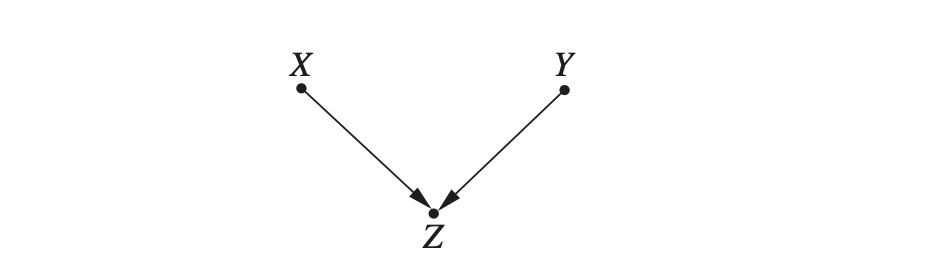
- 구조적 인과 모형 (Structural Casual Model): 방향이 있는 비순환 그래프(Directed Acyclic Graph, DAG)에 기반하여 인과 모형을 구성합니다. 그래프를 하나 만들었다는 것은, 데이터 생성 과정에 대한 어떤 가정을 했다는 것입니다. 예를 들어 위와 같은 그래프를 만들었다면 각각 연결된 노드들 사이의 path에 대해 조건부 확률들을 가지고 모델이 형성됩니다. 이걸 바탕으로 원인 변수에 변화가 생기면 생겨날 Z의 변화량을 측정합니다.
- Potential outcomes: Neyman이 처음 제시했고 Rubin이 발전시켜서 루빈 인과 모형(Rubin causal model, RCM)이라고도 하는 프레임워크입니다. 이 접근 방식에서 인과란 두 가능한 결과를 대조시킴으로써 판단이 됩니다. 즉 우리가 판단하고자 하는 원인이 되는 행동을 어떤 종류의 처치(treatment)라고 한다면, 이 처치가 0이거나 1일 때 가능한 결과들을 각각 $Y_0$, $Y_1$ 로 표현할 수 있습니다. $Y_0-Y_1$ 이 차이가 존재한다면 이것을 X의 Y에 대한 인과성의 존재로 판단하며, 이걸 구하기 위해서는 평균적인 두 결과의 차이, 즉 $E[Y^0_i-Y^1_i]$ 를 보게 됩니다. 이걸 평균 처치 효과(average treatment effect)라고 합니다.
그 외에도 계량경제학에서 주로 사용해왔던 Regression Discontinuity, Difference-in-Differences, Instrumental Variables 등이 있습니다. 다만 본 글의 목적은 인과 추론의 목적과 개념을 소개하는 것이므로 상세한 부분은 (오늘은) 건너뛰겠습니다. 앞으로 가능하면 위 방법들을 차례차례 다뤄보려고 합니다. 우선 Causal Infereince in Statistcs: A Primer (J. Pearl)로 SCM을 살펴볼 예정입니다.