신경망 Backpropagation 계산 그래프 이해하기

밑바닥부터 시작하는 딥러닝 2을 보고 정리한 내용입니다.

• 다 아는 얘기 요약
  • 계산 그래프를 만든다
  • 왼쪽에서 오른쪽으로 계산한다 = forward
  • 오른쪽에서 왼쪽으로 미분 값을 전달하면서 곱한다 = backward
    • 합성함수의 chain rule
    • 장점: 아무리 복잡한 함수를 다뤄도(아무리 많은 함수를 합성해도) 그 미분값은 그 함수를 만드는 각 개별 함수들이 미분을 구한 다음 곱하면 된다!
  • 
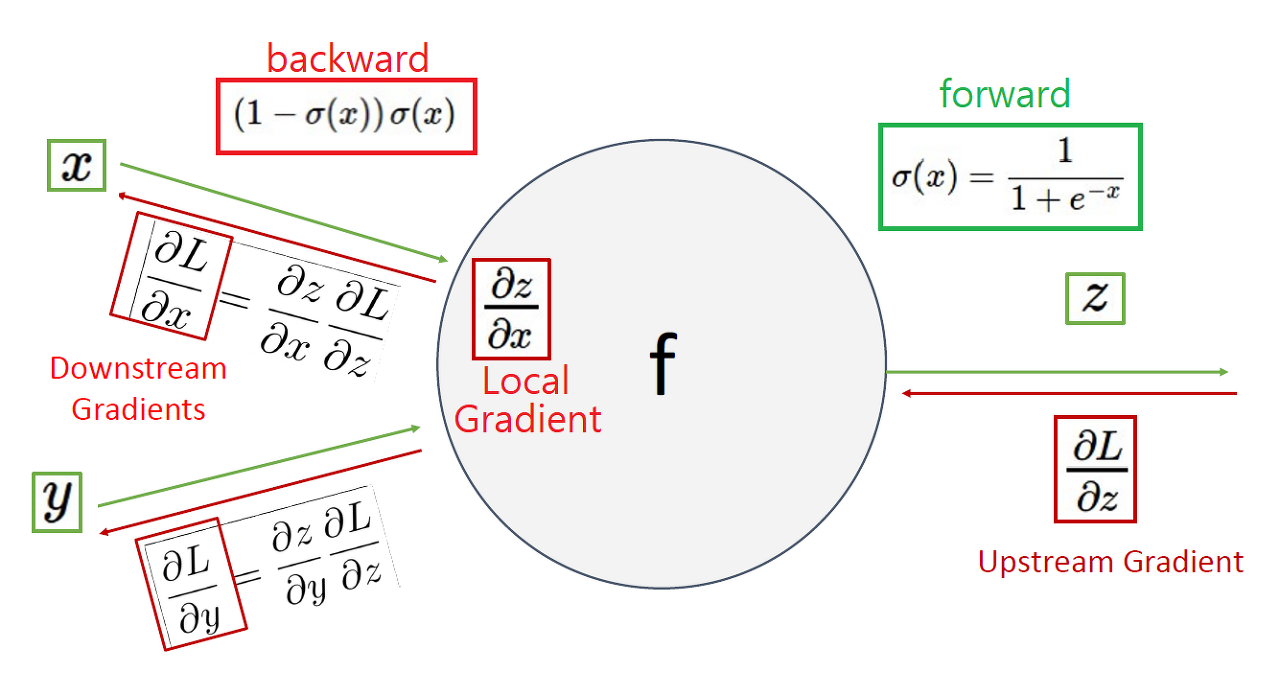
    • 상류에서 넘어온 미분값을 UG (upstream gradient)
    • 이 노드에서 계산되는 미분값을 LG (local gradient)
    • 그 둘을 곱해서 다음으로 넘어가는 값을 DG (downstream gradient) = LG x UG
    • 라고 하자.

기본적인 노드 유형별 backpropagtion

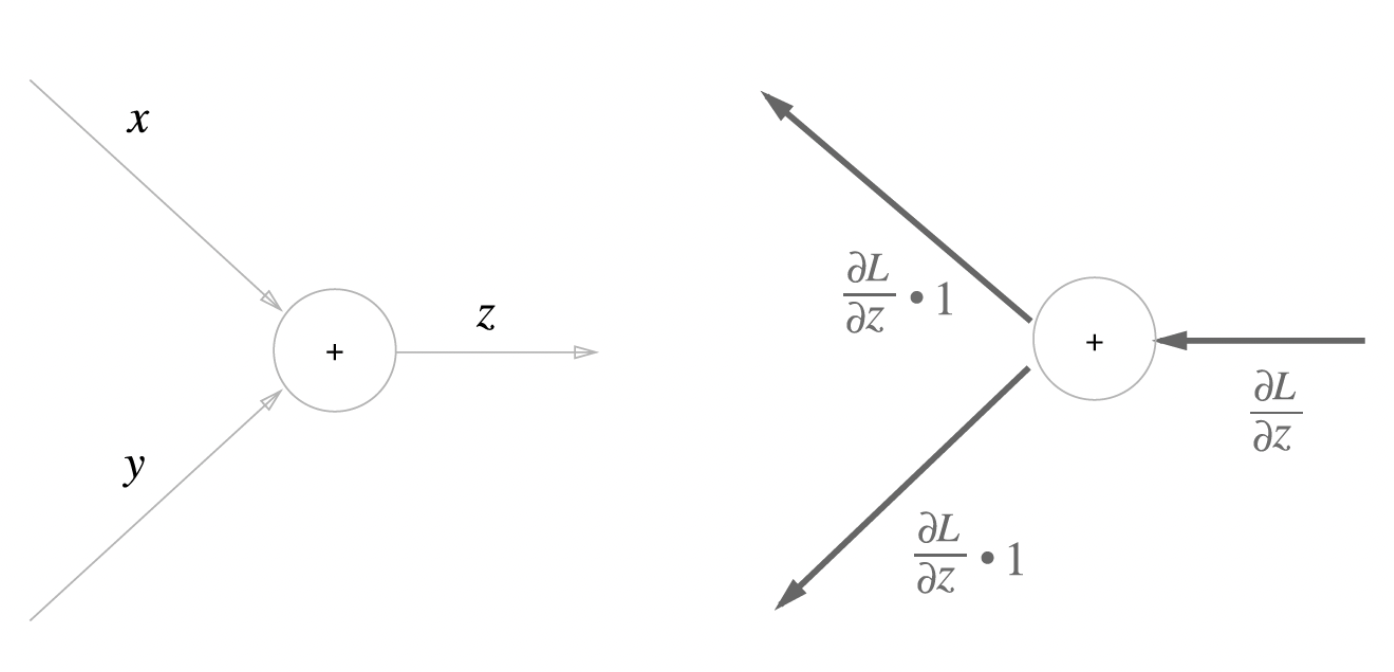
• 더하기 노드
  • LG = 1이므로 DG는 UG를 그냥 그대로 보내준다
    • 
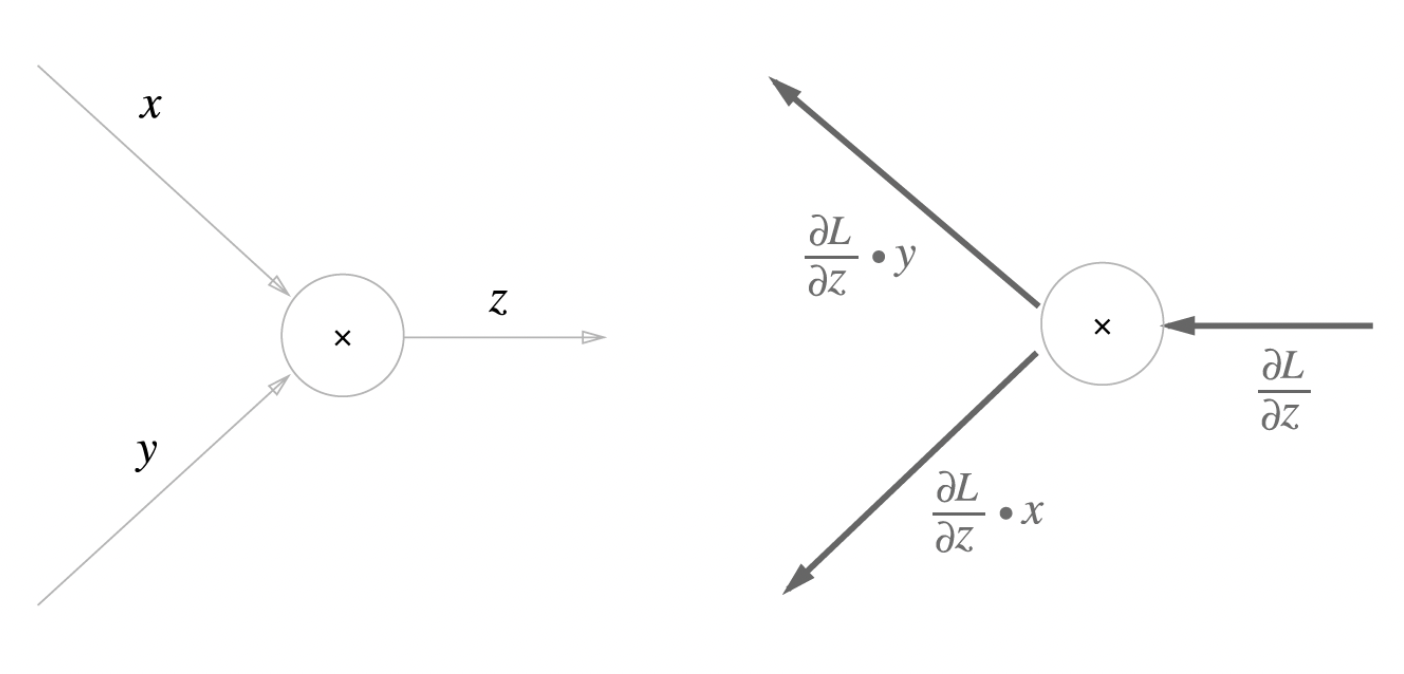
• 곱셈 노드
  • 서로 값이 바뀜. 즉 UG에 순전파 output을 서로 바꿔서 곱해서 보내줌
  • 
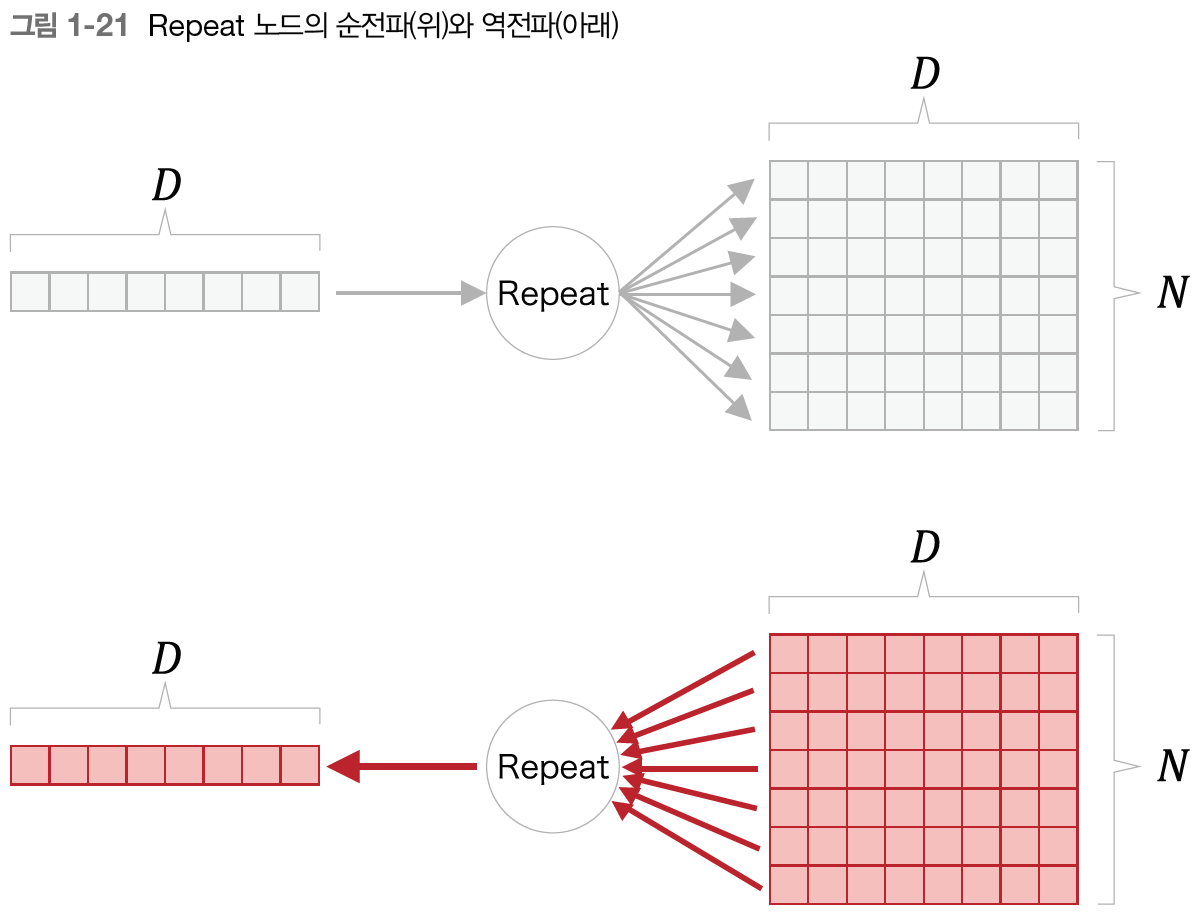
• repeat 노드
  • N개로 복제해주는 노드라면 UG를 모두 더함!
    • 
  • 처음에 이거 좀 이해 안 갔는데 생각해보니 n개의 UG(변화량)을 모두 합해서 알려줘야 함. 즉 이 노드 전의 인풋이 1만큼 변하면 그 뒷단은 n만큼 변하는 거라 합쳐줘야 함
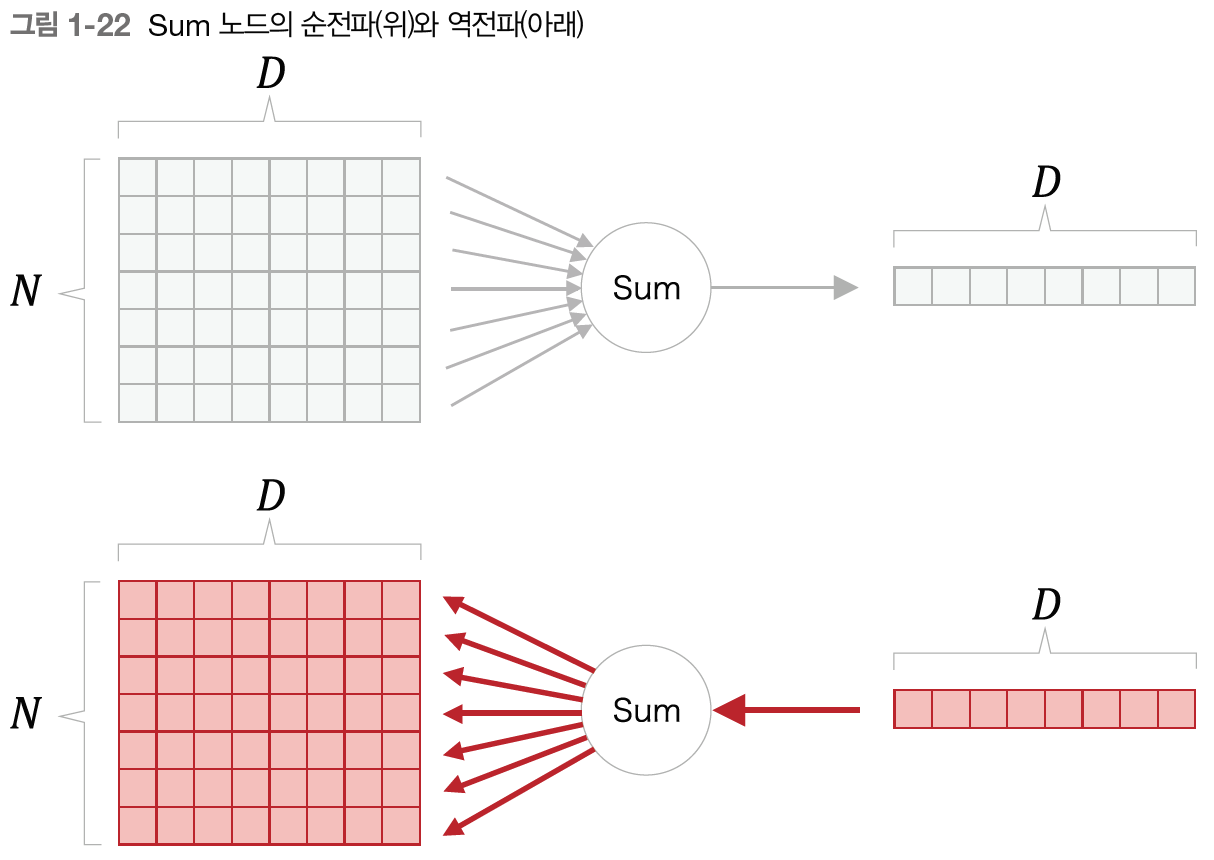
• sum 노드
  • 반대로 sum은 UG를 그냥 모든 노드에 복제해줌!
  • 
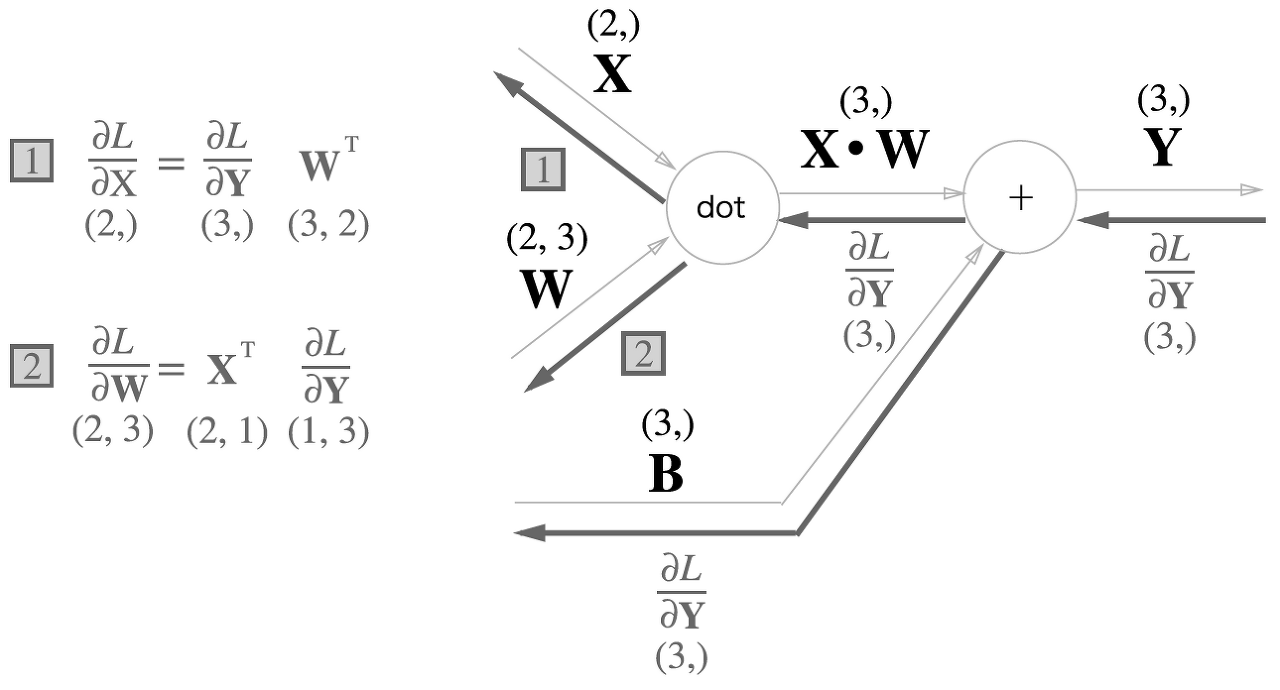
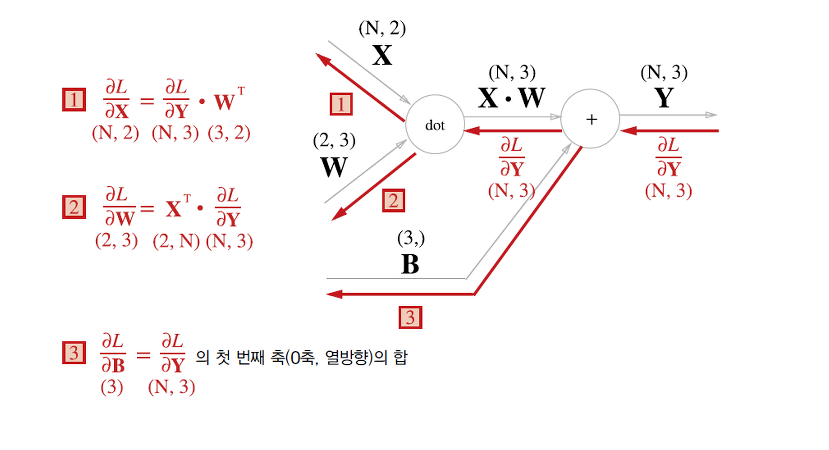
• 행렬곱 노드
  • 
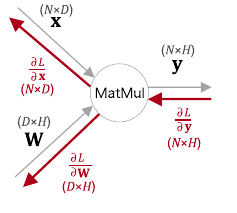
  • $D=2, H=2$ 라고 하자.
  • $x_1$을 조금 변화시켰을 때 L이 얼마나 변할 것인가? $x_1$을 변화시키면 $\mathbf{y}$의 모든 원소가 변하고 그에 따라 $L$이 변하게 되므로 $x_1$에 대한 미분값은 $\mathbf{y}$를 거쳐가는 모든 경로를 더해야 됨
    • $\frac{\partial L}{\partial x_1} = \sum_j \frac{\partial L}{\partial y_j} \frac{\partial y}{\partial x_1}$
  • 이때 행렬곱을 생각해보면,
    • $y_1 = x_1 \times W_{11} + x_2 \times W_{21}$
    • $y_2 = x_1 \times W_{12} + x_2 \times W_{22}$
    • 따라서 $\frac{\partial y_j}{\partial x_1} = W_{1j}$
    • $\frac{\partial L}{\partial x_1} = \sum_j \frac{\partial L}{\partial y_j} \frac{\partial y}{\partial x_1} = \sum_j \frac{\partial L}{\partial y_j} W_{1j}$
  • 즉 $\frac{\partial L}{\partial x_i}$ 는 벡터 $\frac{\partial L}{\partial \mathbf{y}}$ 와 $W$의 $i$ 행 벡터의 내적으로 구해지며 이걸 확장하면 다음과 같음
    • $\frac{\partial L}{\partial \mathbf{x}} = \frac{\partial L}{\partial \mathbf{y}} W^T$

Affine layer

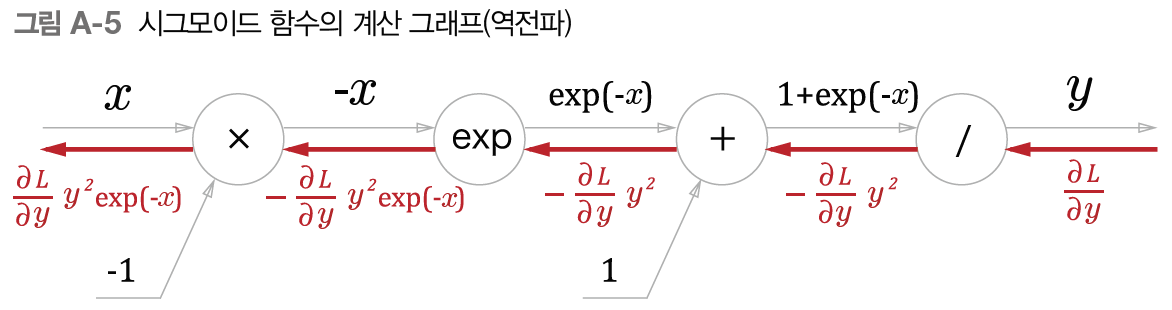
Sigmoid layer

• 뒤에서부터
  • / 노드 : $y=\frac{1}{x}$ 이므로 LG = $-\frac{1}{x^2} = -y^2$
  • + 노드: UG를 그대로 흘려보냄
  • exp 노드: LG = $\exp(-x)$, DG = $- \exp(-x) \times y^2$
  • x 노드: 바꿔서 UG에 곱해주므로 - 붙이기
• 최종적으로 $y^2 \exp(-x) = \frac{1}{1+ \exp(-x)^2} \exp(-x) = \frac{1}{1+\exp(-x)}\frac{\exp(-x)}{1+\exp(-x)} = y(1-y)$
  • $y$ 값(=순전파시의 출력)만 가지고 미분값을 구할 수 있음! 미분 계산이 간단한 것도 시그모이드의 장점

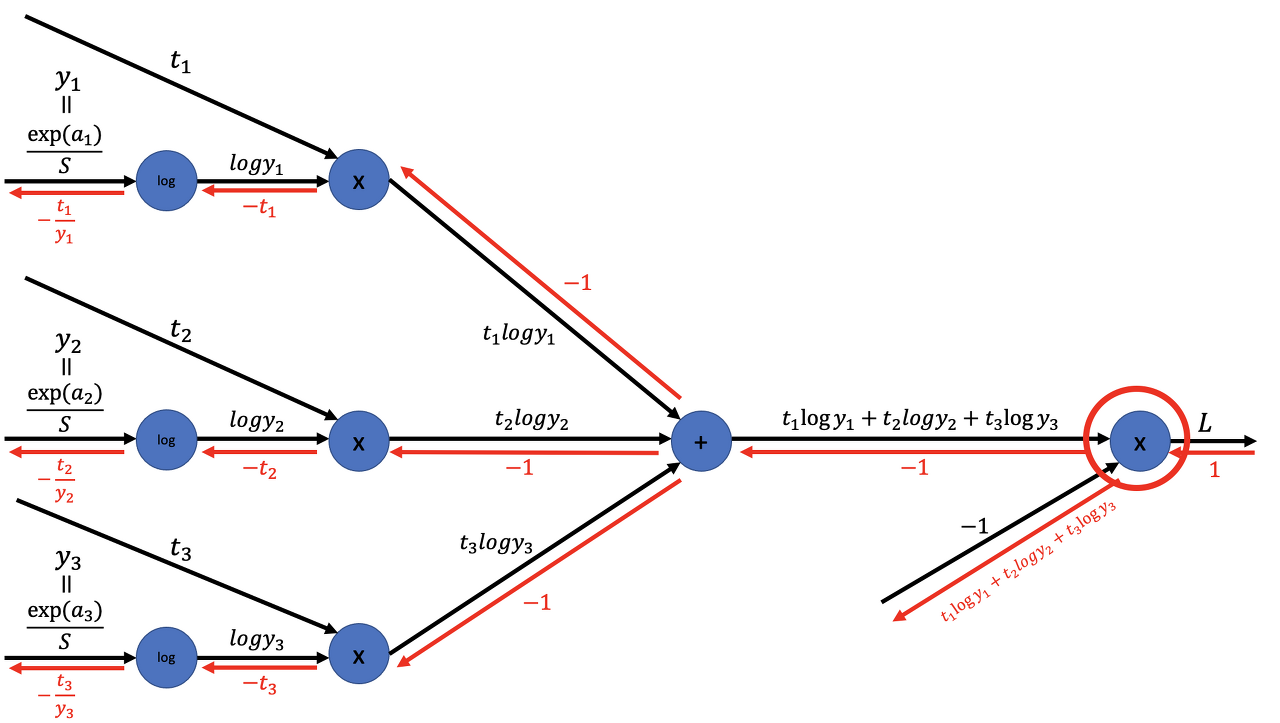
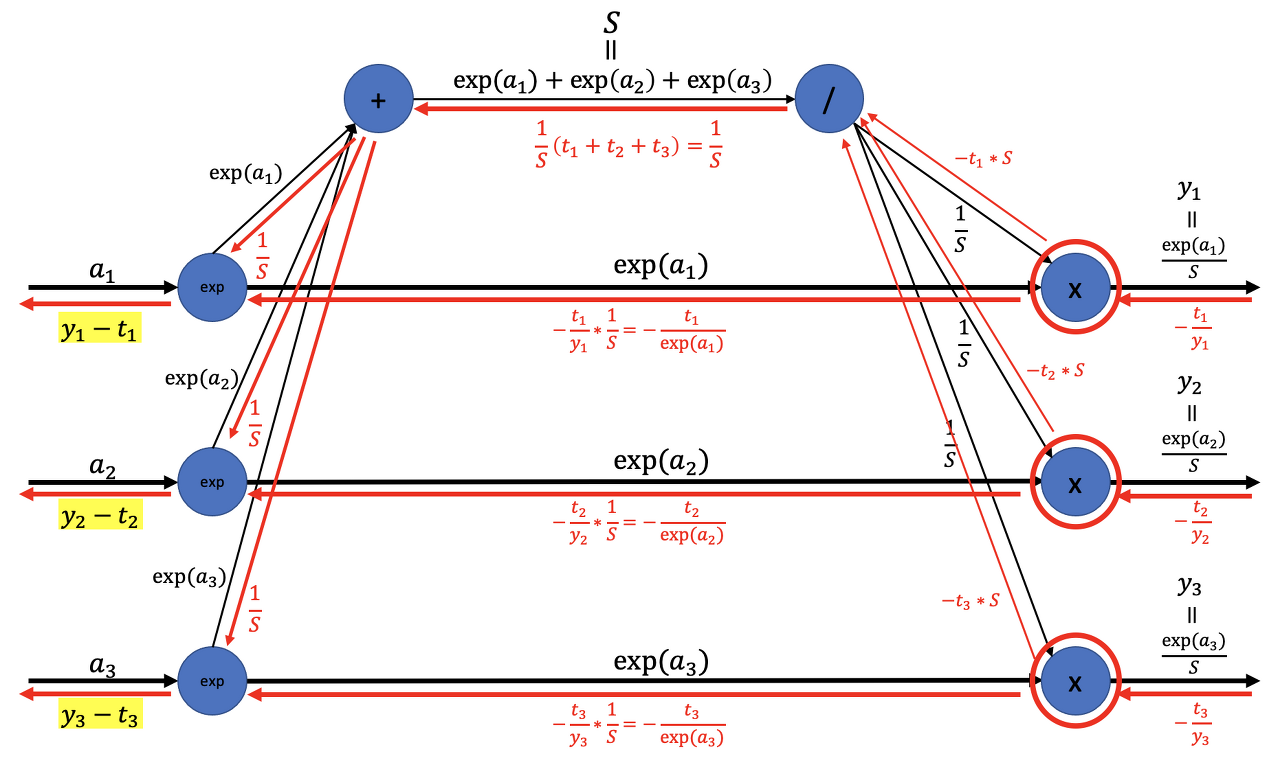
Softmax with cross-entropy loss

• cross-entropy \(L = -\sum_k t_k \log y_k = -\frac{1}{N} \sum_n \sum_k t_{nk} \log y_{nk}\)

그냥 지금까지 한 거 생각하면 다 이해됨. 여기서 $y_i$ 는 softmax 출력임

• softmax \(y_k = \frac{\exp(s_k)}{\sum^n_{i=1}\exp(s_i)}\) $S = \sum^n_{i=1}\exp(s_i)$

• 맨 왼쪽 노드 exp가 이해가 안갔는디
  • 분모를 만드는 쪽이랑 분자랑 합해지는것임!
  • UG가 $\frac{1}{S} + -\frac{t_1}{\exp(a_1)}$로 내려와서, LG인 $\exp(a_1)$ 랑 곱해지면 $y_1-t_1$ 가 됨
  • 그래서 소프트맥스 계층의 역전파는 사실상 예측 아웃풋과 실제 라벨의 차이..! 라고도 볼 수 있다